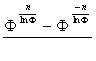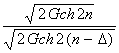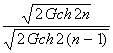|
DYNAMIC SYMMETRY IN NATURE AND ARCHITECTURE Oleh Bodnar Doctor of Art Studies,
Professor of
AbstractThe phenomenon of dynamic symmetry in botanical, the so-called philotaxian, systems is investigated. A mathematical model of phylotaxis grounded on Minkovsky's geometry, as well as the original trigonometric apparatus based upon the golden ratio, are developed. Constant values of phylotaxis dynamic symmetry are defined. The principle of dynamic symmetry in architecture, formulated by D. Hambidge, as well as architect Le Corbusier's Modulor proportional system, are described in terms of philotaxis mathematics.
The term dynamic symmetry
was for the first time applied by the American architecture researcher J.
Hambidge to a certain principle of proportioning in architecture [11]. Later
this term independently appeared in physics where it was introduced to describe
physical processes that are characterized by invariants [10]. Finally, in the
given research the term dynamic symmetry
is applied to regularity of natural form-shaping that in terms of origin
also appears not to be connected with
Hambidge's idea, and, moreover, appearance of this term in physics. However,
all the three variants are deeply interconnected in terms of their meaning
which we are going to show. At first, we point out
strategic similarity of Hambidge's and our researches. This is a well-known
historical direction which in the field of architecture and art is motivated by
the search for harmony regularities and, thus, is aimed at studying the objects
of nature. Usually architects take interest in the structural regularities of
natural form-shaping and, particularly, in the golden section and Fibonacci
numbers which are regularities standing out by their intriguing role in
architectural form-shaping. It is not accidentally that architects who do
researches so frequently pay attention to botanical phenomenon phyllotaxis which is characterized by
these regularities. Phyllotaxis was the focus of
attention of J. Hambidge who is the author of the first variant of the dynamic
symmetry concept. While studying this phenomenon, J. Hambidge introduces a law
of the so called uniform growth and
suggests its geometrical interpretation - spiral
of uniform growth or, in other words, - golden spiral (Fig.
1).
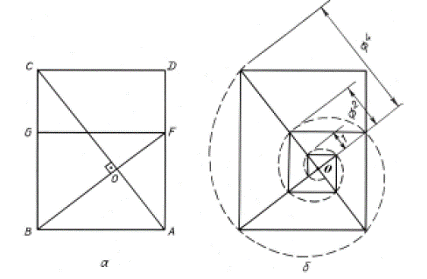
Fig. 1. Building the golden spiral according
to Hambidge. However, the
most important generalization of Hambidge that resulted from his studying the
regularities of natural form-building (phyllotaxis) as well as proportions of
classical architecture comes to the idea of architectural proportioning that is
called dynamic symmetry. J. Hambidge
demonstrates it by means of simple geometrical scheme (Fig. 2).
Fig. 2. Proportional system «Dynamic
symmetry» by J. Hambidge. This
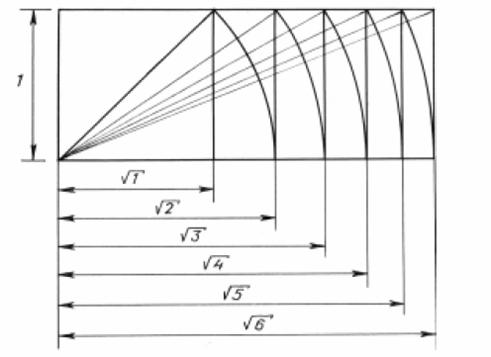
successive system of rectangles the first of which is a square and the next
successive one is built on the side of the original square equal to 7 and the
diagonal of the previous rectangle. Thus, the series of rectangles is formed
with the ratio of sides expressing the series
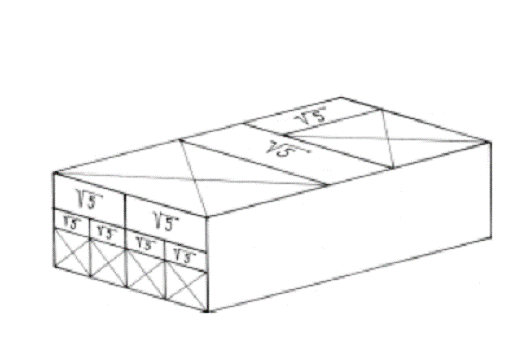
Fig. 3. Three-D model of Parthenon's
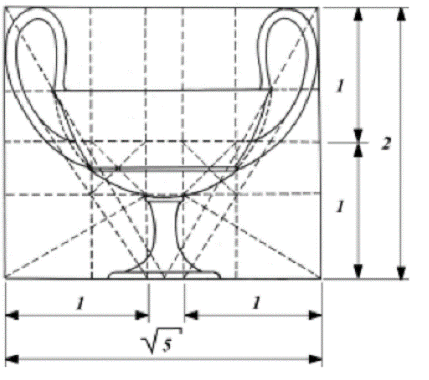
proportions by J. Hambidge.
Fig. 4. Diagram of Greek vase (cantaros) proportions by J. Hambidge. Thus, this is in brief
the essence of J. Hambidge's idea of dynamic symmetry. As one can see, it does
not directly derive from the phyllotaxis properties. Generally, J. Hambidge does
not go deep in mathematics of phyllotaxis. In his various schemes illustrating
the regularities of uniform growth or other ideas of proportioning he applies
well-known numerical relations typical of phyllotaxis, including golden
section. However, his idea of
dynamic symmetry is an original one and in terms of its mathematical content
expresses regularities of quite a general character. It will be possible to demonstrate it after
studying the phyllotaxis research offered below. But before I would like to
predict some possible "unfavourable impressions" that the representatives of
various fields of science may get after reading this text. The author foresees
the possible dissatisfaction on the part of biologists due to schematic layout
and insufficient terminology of biological description of this phenomenon;
mathematicians - who may discover incompliance of symbolics with that used in
phyllotaxis theory; art historians who may be faced with too much mathematical
direction of the research from the viewpoint of art methodology. The author
fully acknowledges all the "troubles" caused by the multidisciplinary character
of the issue. And still, the author
takes on responsibility for the scientific credibility of the results achieved.
The central task of the research is formulated on the basis of minimum initial
information which is sufficient to grasp the essence of the main issue of the
problem and build the research "from scratch" making it independent of the
research experience accumulated in the field. Though, it is worth mentioning
that this experience is quite substantial. The research of phyllotaxis was in
the centre of attention of many mathematicians and biologists. For
instance, in the second half of the 20th
century it was in the focus of interest of H. Cockster [7], Adler [12], Jean
[13], Schwabe [14], Petukhov [9], etc. who in their works created the modern
"mathematical and biological" theory of phyllotaxis. The results of the given
research were first published in 1989 [1]. At that time they were new. At any
rate, none of the researchers describing phyllotaxis applied Minkowski's
geometry and the system of hyperbolic trigonometry. We shall briefly describe this
research. It is known from biology
that mutual arrangement of various primordia
that appear on the cones of spindles is characterized by the spiral symmetry.
This principle of situation that was named phyllotaxis
is also clearly observed in dense inflorescences and infructescences, for
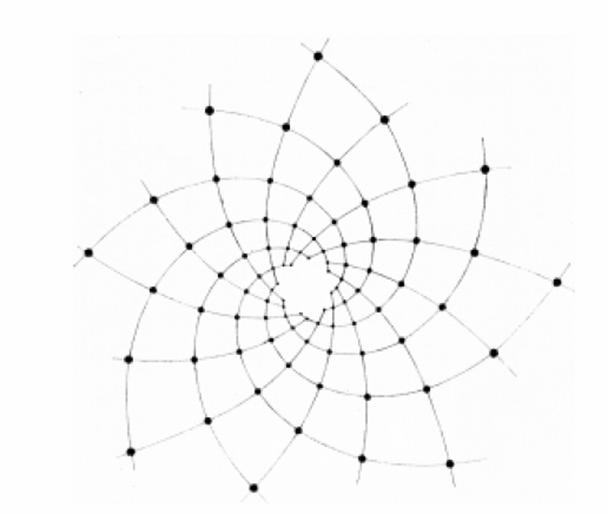
instance, on sunflower discs, pine cones and many other types of bioforms (Fig.
5).
On the surfaces of
phyllotaxis forms, dense inflorescences and infructescences in particular, one
can clearly observe left- and right-wound spiral-like rows of structural
elements (primordia, seeds, leaves). The symmetry order of phyllotaxis forms is
usually shown as the ratio of numbers that corresponds to the quantity of left
and right spirals. According to phyllotaxis law these ratios are described by
the combinations of numbers of recurrent rows which accept the rule: u
n = u n - 2 + u n - 1. Widely spread are the
symmetrical type of phyllotaxis which are described by Fibonacci series: …, 0, 1, 1, 3, 5, 8, 13, 21, 34, … . Numbers of Lucas series …, 1, 3, 4, 7, 11, 18, 29, 34, … are also quite
frequently realized in phyllotaxis, seldom - numbers that belong to the series …,
4,
5,
9,
14,
23,
…
. The order of symmetry in case of Fibonacci phyllotaxis (F-phyllotaxis) is
expressed by the ratios: It is typical that in
symmetry cases always there are neighboring numbers of the series. In certain
cases, when on the surfaces of the pattern one can single out three groups of
spirals, the symmetry is shown by means of three numbers. As a rule, the
off-shoots of plants and trees are characterized by the low order of symmetry
while the inflorescences and infructescences - by high symmetry order. For
instance, the order of symmetry with sunflower can be up to The interesting indicator
of phyllotaxis structures is the so called D divergence which is the angle of
splitting of twosubsequent primordia. Divergence
measured in circle fractions in case of F-phyllotaxis is always expressed by
the same number that is the pattern order of symmetry, i.e. it can be equal Some types of phyllotaxis
patterns while growing subsequently change (expand) the order of their
symmetry. It is this peculiarity of phyllotaxis that we name dynamic symmetry. As an example, one can take the sunflower. The sunflower heads
arranged on the various levels of one and the same stem have different
symmetry: the higher the level, i.e. the older the disk, the higher its order
of symmetry is. In symmetry dynamics the following sequence is realized: … ® With the change of symmetry the
divergence angle changes respectively. Still on all the disks regardless of the
number of spirals the so called conforming
(angular) characteristics of spiral
patterns appear to be the same, that is - the spirals cross at a straight
angle. This
data is enough to identify the objective of the research. It means to
geometrically decipher the phyllotaxis pattern formation process and the key
issue is how the symmetry changes. At the beginning it was
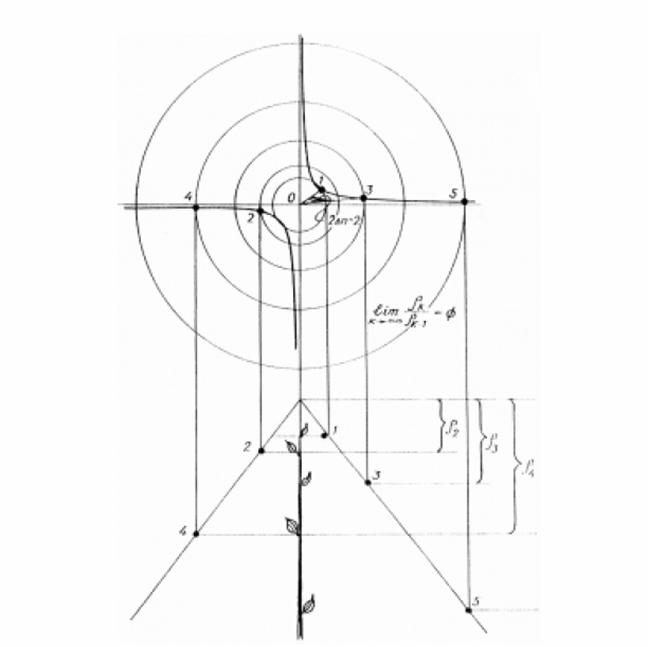
necessary to do a simple geometrical stylization of phyllotaxis surface and
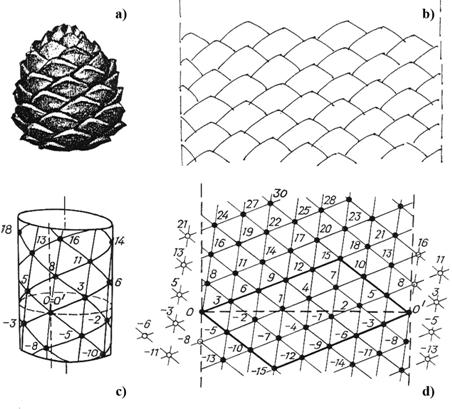
represent it as a regular flat lattice (Fig. 4). This lattice (Fig. 6d) is
numbered in such a way that the numbers of vertices characterize their distance
from the straight line 00'; at the same time per unit is
accepted the distance to the nearest from 00' point 1. Due to this numbering
rule the order of symmetry of cylindrical lattice in the system of numerical
denomination is expressed in the following way: points adjacent to 0
are numbered 5, 8 and 3 (also -5, -8 and -3), i.e. such numbers
that characterize numerical structure of helical spiral of cylindrical lattice. It is obvious that for
the lattices with different symmetry the numbers of neighboring vertices of O
point will be different. We shall do the
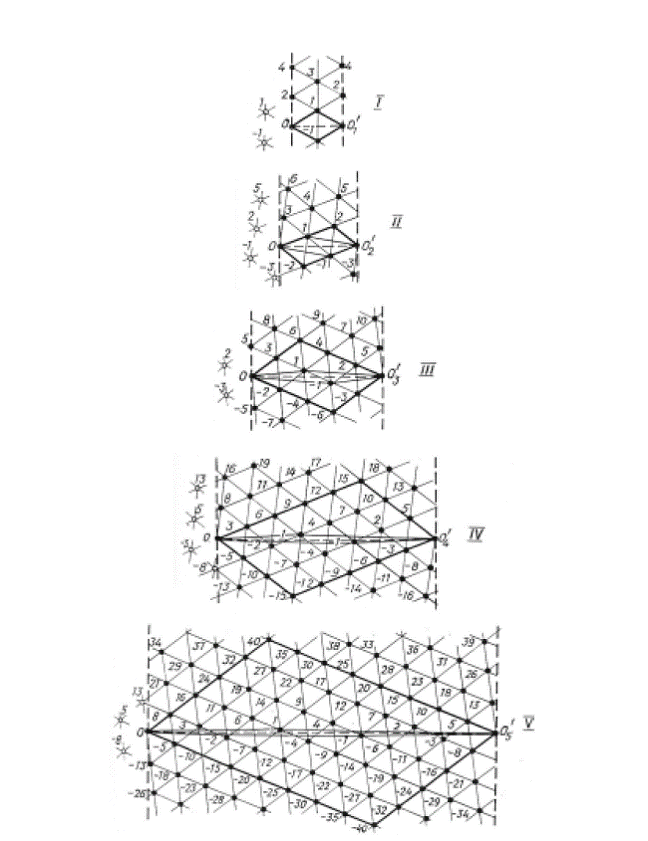
comparative analysis of the series of lattices illustrating the sequential
stages of symmetry change in phyllotaxis (Fig. 7). According to their metrical
features, all the lattices are the same. Thus, the peculiarity of natural
phyllotaxis lattices to renew their conforming characteristics at any stage of
symmetrical development is taken into account. It is obvious that for
the lattices with different symmetry the numbers of neighboring vertices of O
point will be different. Movie installation No 1
Fig.6. Analysis of structural and
numerical features of phyllotaxis lattice: a -
general look of cedar cone; b -
scheme of unrolling; c -
cylindrical lattice - idealized form of
cedar cone; d - unrolling of cylindrical
lattice We shall do the
comparative analysis of the series of lattices illustrating the sequential
stages of symmetry change in phyllotaxis (Fig. 7). According to their metrical
features, all the lattices are the same. Thus, the peculiarity of natural
phyllotaxis lattices to renew their conforming characteristics at any stage of
symmetrical development is taken into account. Let us trace the
regularity of transformation of parallelogram 010'
Fig.7. The series of unrollings illustrating sequential stages of cylindrical
lattices symmetrical transformation. All the schemes depict parallelogram OII'O'
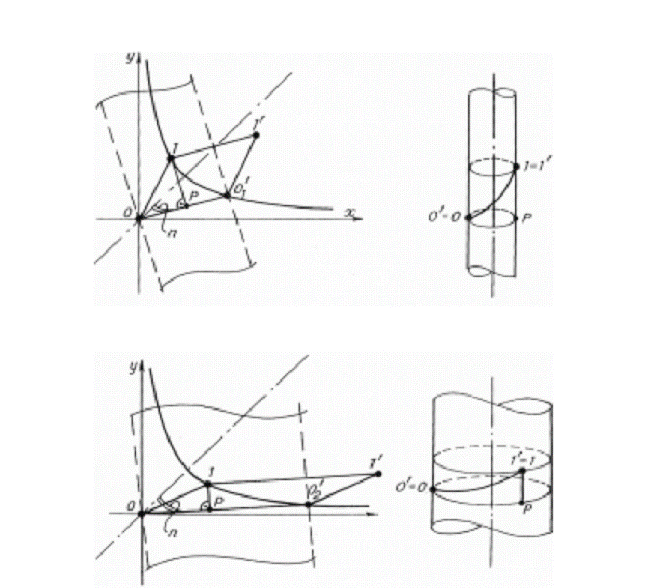
Fig.8. Research of elementary parallelogram transformation regularities. The building rule is that
sides of every parallelogram (starting with the third one) are diagonals of two
foregoing parallelograms. As any two successive parallelograms have three
common vertices, it is obvious that all parallelograms have equal square.
Preserving the square is the first interesting feature of parallelogram dynamic
transformation. The second is that straight lines are parallel: parallelogram
at any stage of transformation still is a parallelogram. Here one can draw the
key supposition of the research - preservation of square and parallelism of
straight lines are the features of hyperbolic rotation. It means we deal with
hyperbolic transformation. It is necessary to specify this idea.
Fig.9. Transformation of elementary
parallelogram by means of hyperbolic motion. Fig.10. Scheme of lattice
transformation by hyperbolic rotation. . Figures 9 and 10
illustrate "binding" of the lattice to the scheme of hyperbolic transformation. Movie installation No 2. Thus, we can state that
hyperbolic rotation is the basis of symmetry transformation illustrated on Fig.
7. This is the key finding of the research that allows to develop an entirely
new look at the issue of phyllotaxis geometry. First of all, within the
framework of the idea of hyperbolic rotation it is necessary to conduct a
specific analytical and geometric research of a regular lattice. Immediately an
interesting fact is revealed - in metrical characteristics of the lattice
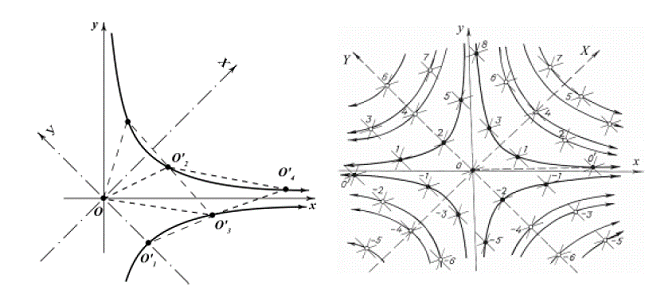
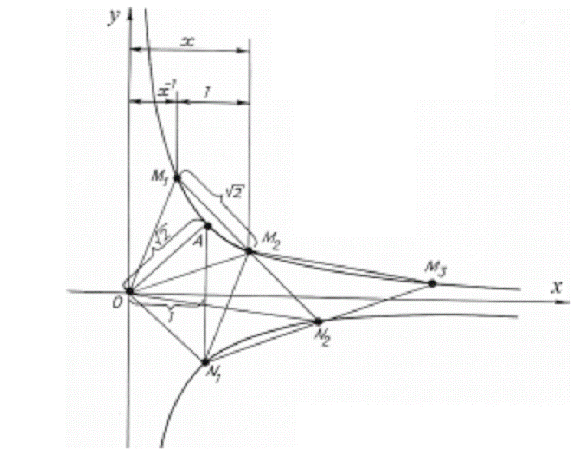
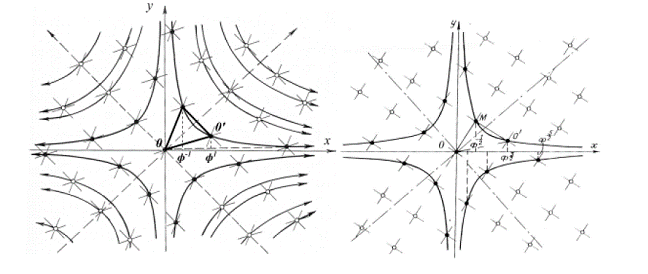
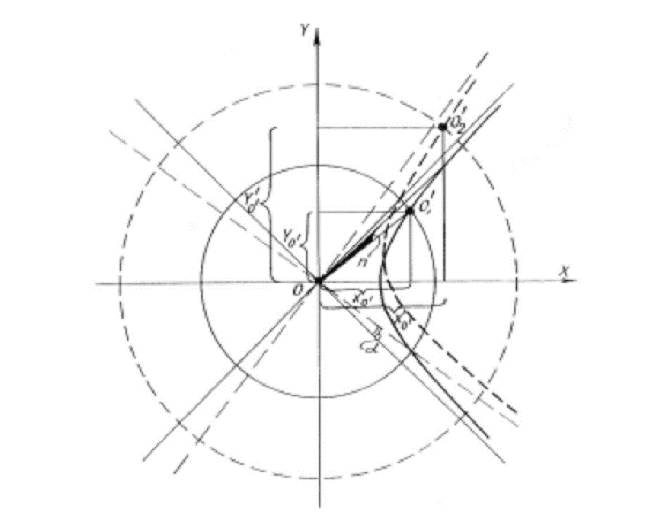
organically present is the value of the golden section. (Fig. 10). Let us have a look at Fig
11. Here the arrangement of vertices corresponds
to the Fig. 5.9, 5.10 and is characterized by the following conditions: : xA = points М1 and М2 are symmetrical as to 0А; 0М1М2N1, 0М2N2N1, 0М2М3N2 are parallelograms, that means that 0N1
= М1М2 = 0A =
Fig.11. Analysis of
lattice metrical features. Let us determine the
abscissa of the point М2, marking х - х - 1 = 1, х2 - х - 1 = 0, х = As follows from the
statement of the problem х = where а - is the semi-axis of hyperbole that
the point under consideration belongs to. Moreover, if for the angular unit (module)
of hyperbolic rotation one takes the angle dividing two neighboring
transformation stages (for instance, stages I and II, II and III, III and IV,
etc. - Fig.7), in other words, the smallest angle, the rotation to which will
result in the self-alignment of the
lettice, then the exponent n
will coincide with the value of hyperbolic angle (in modules), characterizing
the position of the point under consideration (Fig. 12).
Fig.12. Determining the module of
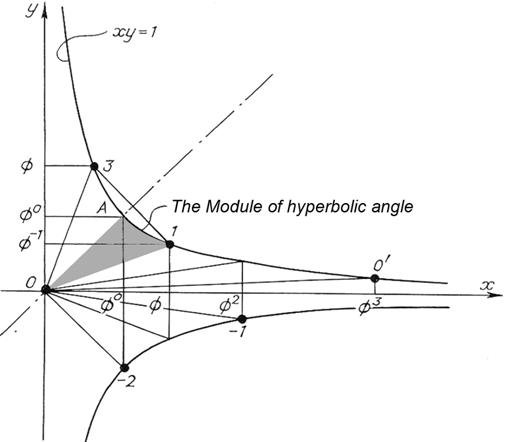
hyperbolic angle. In the coordinate system X0Y
the formulae of the coordinates of the arbitrary point look like hyperbolic
functions: X = a · As one can see, these are unusual hyperbolic functions as both the base F and the value of hyperbolic angle unit here differ from the accepted ones*. (* In classic variant hyperbolic angle unit is the square of the so called coordinate rectangular of the hyperbole point М, that is formed by the coordinate axes and the straight lines that were drawn through the point М in
parallel to the coordinate axes. If the hyperbole equation is xy = 1, then the square of the coordinate rectangular is numerically equal to 1.
If unit square pertains to the hyperbolic sector 0АМ (А - hyperbola vertex), then xM = e, and yM = e - 1.) Therefore, these
functions have independent signs and names: for for for The golden functions
preserve the main features of the "classical" hyperbolic functions and
accommodate with them taking into account the dependence between numbers F
and е (F = e ln F, F n = e n ln F,). For instance:
Formulae (2) of the
coordinates of the arbitrary point in the system X0Y now can be written
like that: X = a ·
Gch n, Y = a · Gsh n. (3) Changes of arbitrary
point coordinates caused by the hyperbolic rotation are expressed by the
formulae: x' = X · Gch n + Y · Gsh n, y' = X · Gsh n + Y · Gch n. (4) In the process of
hyperbolic rotation the lattice is deformed, but periodically, through rotation
module the same metric states are repeated. Fig. 13 illustrate the
subsequent deformation stages of the lattice elementary triangle which are
fixed through half-module of the rotation. The metric peculiarities of the
triangle are obvious. Fig. 14 show full lattice depictions in two extreme
states. In one of them (Fig. 13) the elementary triangle gets the sizes Movie installation No 3. As one can see, the
transformation of the lattice by means of hyperbolic rotation is characterized
by periodicity. Two rotation modules are considered to make a full period (cycle). It is necessary to note that the lattice
state is repeated through one module, however two such states do not coincide,
they are in mirror position as to the hyperboles symmetry axes. It is important to state:
hyperbolic rotation is symmetry transformation of a regular
lattice. This transformation is not
considered in the classical theory of symmetry.
Fig.13. Characteristic
conditions of lattice elementary triangle.
Fig.14. Two extreme
conditions of the lattice. It is also necessary to
focus on the following issues. 1)
Unlike the circular rotation when the lattice knots preserve strict mutual
arrangement, the process of hyperbolic rotation leads to the changing of the
mutual arrangement of the knots. 2).
For the symmetric transformation the lattice should be placed onto the
hyperplane in a special way. In general, the basic lattice lines should not
coincide with asymptotes. Fig. 15 (as compared to Fig. 14) illustrates the
effect of such "non-phyllotaxis" transformation. We shall not concentrate on
this important point deserves separate consideration. Let us continue the
research.
Fig.15. Transformation
effect when asymptotes go through the lattice knots. Following the principle
of lattice numeration the number of any of its points in the coordinate system
where abscissa axis coincides with the direction 00' (Fig. 6, 10), is
numerically equal to its ordinate. We have developed formulae to describe the
coordinates of arbitrary vertex in the system of movable coordinates x'0y'
(Fig. 16).
Fig.16. Determining coordinates of
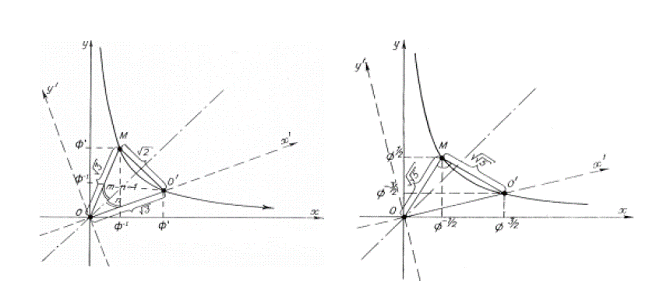
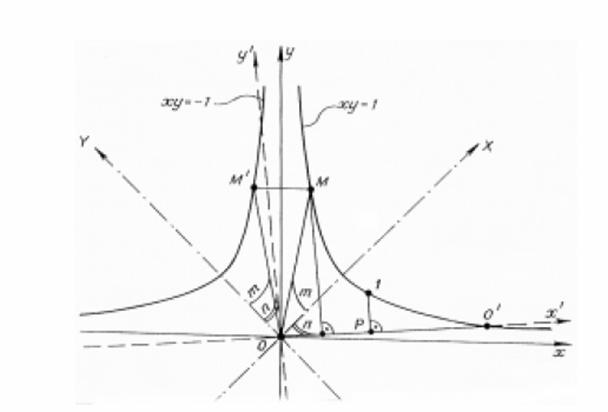
the arbitrary point in the system of movable coordinates X'oy'. With any position of the
coordinates the ordinate of the point 1 nearest to 0x' is taken as a unit of
measurement. Thus, for vertices that belong to the hyperbole xy =
1, we have: x'M = y'M = where m - hyperbolic
angle X0M, n - hyperbolic angle X00'.
For vertices that are situated on the hyperbole xy = - 1, the
coordinate formulae will be the following: x'M' = y'M' = Thus, in formulae (5) and
(6) we have got an interpretation of the numbers of those lattice vertices that
slide on the hyperboles nearest to the asymptotes. But the analysis of Fig. 10
shows that the numbers of these vertices are Fibonacci numbers. Taking for the
sake of simplicity m + n = k and keeping in mind that the successive vertices are
situated on the neighboring branches through rotation module, one can come to
the following correspondence: F1 = F3 = F5 = F7 = . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . Fk = In the lattice system
different recurrent number sequences are realized on different hyperboles.
Introducing the hyperbole scale ratio (g) one gets the generalized variant
of formulae (7): uk = g · There is another way of
representation of the general member Here A and B
are the so called initial sequence
elements; if recurrent sequence is viewed as an infinite sequence, for
instance, …, 12, -7,
5,
-2,
3,
1,
4,
5,
9,
14,
…
, then initial will be two first numbers of sequence part of fixed signs. In
this case A = 3, B = There is another way of
obtaining trigonometric interpretation of Fibonacci numbers. There is one
interesting arrangement of coordinate axes - X'0X' that is given by
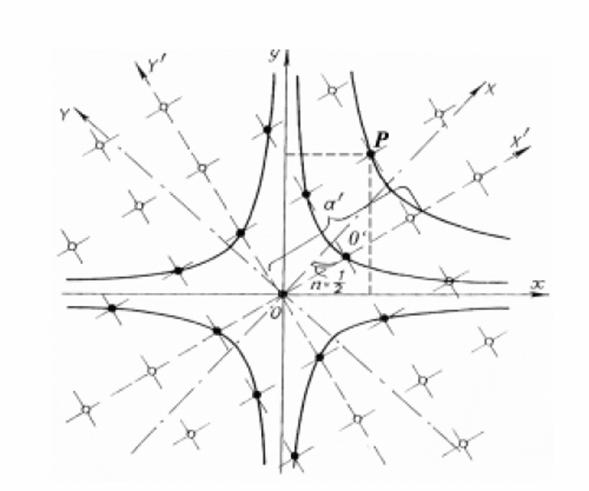
the directions of square lattice (Fig. 17).
Fig.17. Analysis of
lattice in the system of coordinates
X'OY'. Here hyperbolic angle X0X'
is equal to half of the module. If the unit of measurement is the side of cell
square, then the coordinates of X' and Y' lattice knots will be
integers. It is evident. For the arbitrary vertex P we have: X'P = a' · Y'P = a' · Here a' -
hyperbole radius (the orbits of point P) that coincides with 0X'
axis. If the counting of angle is done with respect to 0X' axis, then formulae
will look like (10): X'P = a' · Y'P = a' · where Y = m + This will result in
formulae (7) and (8) that correspond to the special case, in particular, when
the vertices belonging to the hyperbole that is the nearest to the asymptotes,
for which a' = Between the
integral-valued coordinates X' and Y' there is a dependence X'2 + X' · Y' - Y'2 = a'2. (12) In fact, it expresses the
hyperbole equation in reference to the coordinates X'0Y'. At the same time,
as the variables X' and Y' successively take on the values
of the adjacent numbers of a certain recurrent
series, the equation (12) illustrates an important feature of recurrent
series, which, taking into account the specificity of formulae (10) and (11),
is recorded in the following way: |uk2 + uk
· uk
+ 1 - u2k + 1| = const. (13) It is obvious that every
series has its own corresponding constant. Thus, we have got new
mathematical interpretation of numerical properties of phyllotaxis dynamic
symmetry. As we see, symmetry indicators
in phyllotaxis are the integral-valued expressions of golden hyperbolic
functions and dynamics of these indicators is presupposed by the regularity
of integral-valued growth of golden functions. In this case formula (13)
expresses the numerical constant of dynamic symmetry. In particular, for F-phyllotaxis
this constant will be 1: |Fk2 + Fk · Fk + 1
- F2k + 1| = 1. The phenomenon of
divergence also undergoes mathematical interpretation. At the beginning we
claimed that divergence angle value in case of F-phyllotaxis numerically
coincides with pattern symmetry order, i.e. the divergence angle is changed
together with the change of symmetry. Let us consider Fig. 18. We shall analyze
the deformation character of the elementary parallelogram 011'0' of the flat
lattice. Here there are two important peculiarities. Firstly, in the process of
transformation the parallelogram square is preserved: 0P · 00' = const;
secondly, the deformation bring about the parallel shift of the bases 00'
and 11'. On the cylinder surface
the elementary parallelogram is transformed into the so called elementary belt, therefore it is clear
that in the process of transformation such
elementary belt will concentrically increase and decrease as to its
height (the square will be left unchanged) and simultaneously there will be
relative angular displacement of its bases that corresponds to the parallel
shift on the involute. Such angular displacement will take place in every
elementary belt and this will stipulate the torsion effect on the cylinder surface in general. The formula of divergence
angle comes from the ratio
The transformations
result in: D = Also
As we see, the angle
limit corresponds to the known value of the so called ,,ideal angle" of F-phyllotaxis.
It is worth noting that in various ,,non-Fibonacci" сases the divergence angle limit has
various values but in all the cases it changes according to the hyperbolic
tangent law.
Fig.18. Analysis of
hyperbolic transformation of cylindrical surface. In the analysis process
we have also understood the transformation character of the cylinder surface in
the process of symmetrical transformation of the cylinder lattice. It is
possible to state that this transformation results in three interrelated
motions: concentric widening of cylinder along its axis, compression along the
axis and torsion. We shall specify the
geometric regularity of cylinder transverse circumference transformation. The
radius r of the circumference 00' is increased according to the
hyperbolic cosine law: r == OO' = It is obvious that any
point of the circumference can be simultaneously presented as the end of the
hyperbole movable radius as well as the end of the circumference movable
radius. This peculiarity finds its analytical expression in the following: X' = X (Gch n · cos a ± Gsh n · sin a) + Y (Gsh n · cos a + Gch n · sin a), Y' = X ( - Gsh n ·
sin a + Gsh n · cos a) + Y (Gch n · cos a
Fig.19. Analysis of
transformation of cylinder transverse circumference. With n = 0 we have the
formulae for coordinates' transformation that results from the circular
rotation: X' = X · cos a + Y · sin a, Y' = - X · sin a + Y · cos a. With a = 0 we
have the formulae for coordinates' transformation that results from the
hyperbolic rotation: X' = X · Gch n + Y ·Gsh n, Y' = X · Gsh n + Y · Gch n. These formulae reflect
the complex motion of the point that is simultaneously a circular and
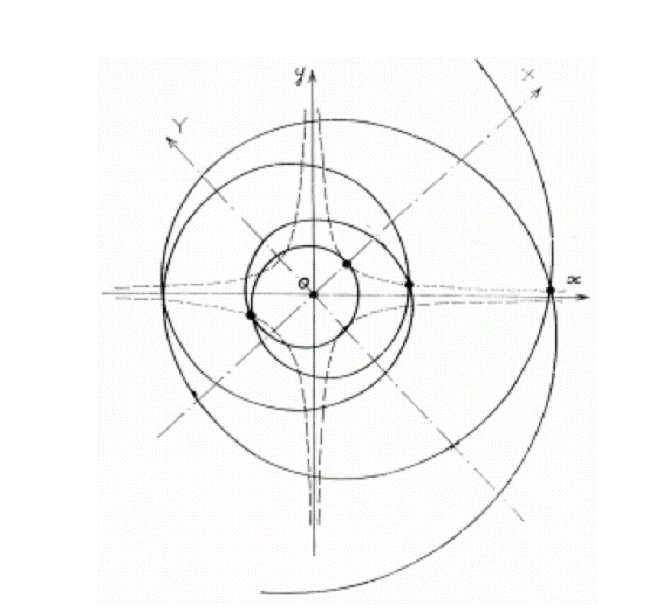
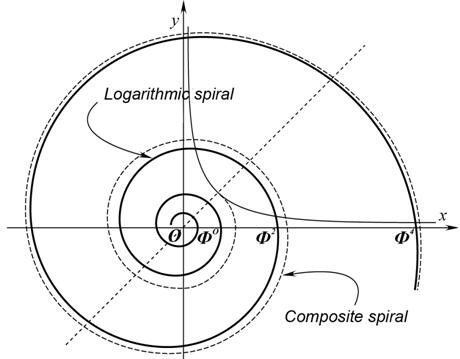
hyperbolic motion. The trajectory of such a motion is a self-intersecting
spiral which can be called a composite one (Fig.
20), because it actually illustrates the composition of two rotations.
Fig.20. Composite
spiral for which Thus, the very composite
spiral is an expression of geometrical law of cylinder transverse circumference
transformation. It finds its laconic representation in a formula:
which shows the main peculiarity of
composite transformation, namely, consistency of angle speeds of hyperbolic
rotation (w h = Thus, we have presented
the main findings of the phyllotaxis research that contain mathematical
explanation of the dynamic symmetry of this phenomenon and allow to generalize
on different variants of interpretation of the dynamic symmetry phenomenon,
particularly, in architecture. However, aiming to fully
present the mathematics of phyllotaxis we shall briefly mention some other
elements of this research. It is necessary to stress that the research was
about cylindrical phyllotaxis. But
this is only a preliminary stage of theoretical idealization of phyllotaxis. Cone is considered to be more adequate
generalization of phyllotaxis pattern. Cylinder as well as disk is considered
to be the special case of cone determined by the extreme values - 0 and We shall remind the
essence of the existing ideas about geometrical features of phyllotaxis cone
lattices and dynamic mechanism of their pattern formation. It is generally
considered that the structure of phyllotaxis cone lattices (arrangement of the
vertices) is subject to the law of logarithmic spiral [2, 5, 6]. Thus, to the
logarithmic spiral also belong parastichy that form lattices on cone and
disk-like patterns and the so called basic
(or genetic) spiral that
successively runs through all the lattice vertices. Such lattices will be
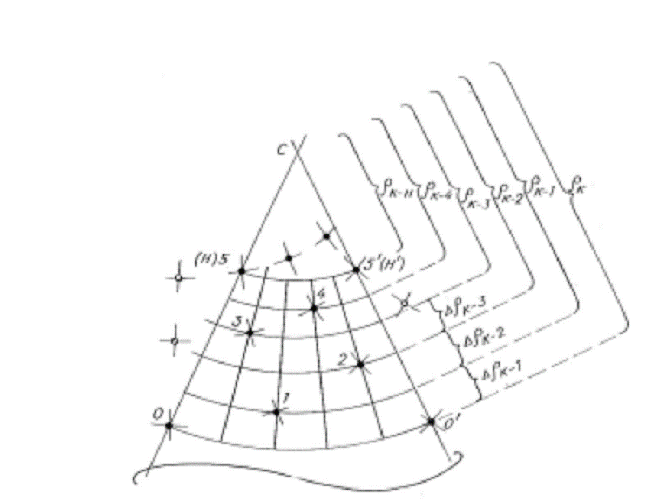
called logarithmic. Structural and semantic
character of the lattice is determined by the two indicators qл - ratio of local similitude that can
be found from the ratio qл = qл = q D, (18) where q - ratio of the basic spiral
similitude.
Fig.21. Analysis of
the general case of logarithmic lattice. Correspondingly, the
algorithm of logarithmic lattices pattern formation goes to indicating the
primordia motion trajectory, i. e. basic logarithmic spiral and the so called primordial growth interval Dt, or to the intensity of their reproduction N (it is meant that N = w з = So, this is the classical
model of phyllotaxis pattern formation. The findings of
cylindrical phyllotaxis research result in a principally different idea of cone
lattices modelling. The idea is that the fundamental regularity of the
structural organization of cone phyllotaxis is composite (and not logarythmic) spiral. Parastichy in reality are composite spirals. The same is
genetic spiral. Cone transverse circumference transformation also occurs
according to the law of composite spiral. Lattices formed according
to the composite spiral law are called natural
lattices (Fig. 22).
Fig.22. Example of
natural lattice with 8:13 symmetry. They resemble logarithmic
ones but, in fact, they are incompatible with them. The reasons and character
of this incompatibility can be explained on the comparative drawing of
logarithmic and composite spiral (Fig. 23).
Fig.23. Comparative
drawing of logarithmic and composite spiral. As we see, the
logarithmic spiral is a peculiar asymptote for the composite one. Different
features of logarithmic and natural lattices are explained by different
mathematical nature of these two curves. The natural lattice is characterized
by the initial scale, which is
defined according to the smallest radius of genetic spiral. Evidently, the
notion of initial scale does not have any value in reference to the logarithmic
lattice. Of principal importance
for the natural lattices is the fact that indicators qл and D in their structure are
not observed in the ideal situations. They only come close to the nominal
values as they withdraw from the centre. In the zone of centre of divergence
from logarithmic regularity they are evident. In fact, this is violation of similitude.
We can specify the divergence regularity. For instance, for qл this regularity is determined by the
change of ratio Before considering a
specific example let us once again stress that the process of lattice pattern
formation is determined by the formula Now let us consider Fig.
24. It shows ,,top view" and ,,side view" of the natural cone lattice with 1 : 1
symmetry. In this case Da = p , Dn = 1. Let us find the ratio limit qл = Here are specific data
for several initial points:
Fig.24. Scheme that
explains the origin of the Golden section in the off-shoots structures. We have specially chosen
the simplest example which one often observes in nature - on trees and plants
off-shoots. It also explains mathematical reasons for the origin of golden proportion
in the linear correlations of off-shoots structures, in particular, the fact
that proportion discovered in off-shoot natural measurements in fact
approximates golden section. Here golden section cannot be realized in its
absolute value. And some more words about
natural lattices symmetry transformation. We shall not describe it in details
but emphasize that this transformation is based on composite motion - composite
rotation that combines both hyperbolic and circular rotation. This issue will
be discussed in a separate article. Finally, we shall do the
generalizations. Besides Hambidge's variant we shall use in our comparative
research another theoretical result which is well-known in architecture -
Modular of French architect of Le Corbusier.
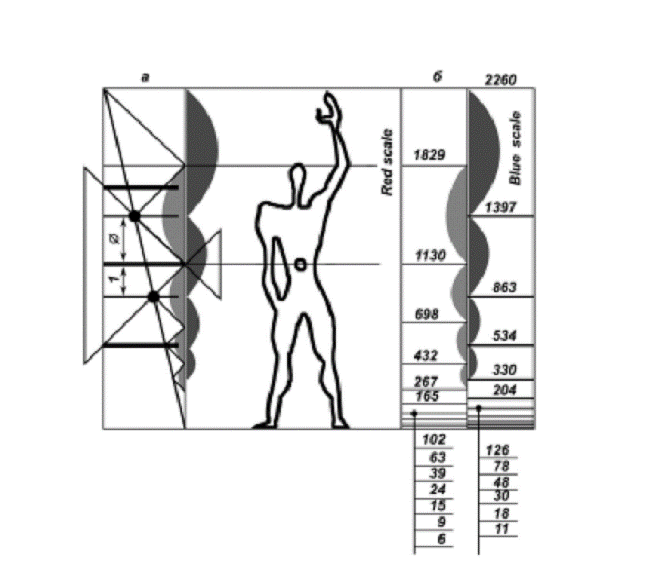
Fig.25. a - scheme of continuous
section division in the golden proportion. B
- integral-valued scales that were obtained as a result of approximation
of irrational scales values. Fig. 25 on the left shows
the scheme suggested by the author of Modular to illustrate the infinite
division of section in the golden proportion. Le Corbusier links such a
division to the proportions of human figure. On the right side of the drawing
one can see the so called red and blue scales where irrational numerical
values obtained by means of infinite division scheme are represented in
approximated integral-valued way. It is clear that irrational numbers express
the golden exponential function. Integral-valued sequences onto which Le
Corbusier transfers the additive features of the
golden sequence can be considered recurrent to a certain degree of
conventionality. Le Corbusier presents the formulae of red and blue scales in
the following way: a n = k ∙ F n, b n = 2k ∙ F
n, where n is an arbitrary
integer; k - dimension factor equal He also accepts that: a n -
2 + a n - 1 = a n, b n -
2 + b n - 1 = b n. Naturally, due to
approximation on certain section of integral-valued sequences additivity is
violated: the golden sequence and its integral-valued approximations ideally
cannot coincide as they express various mathematical regularities. But we have to show how
to adjust the imbalance. Modular irrational and integral-valued scales are to
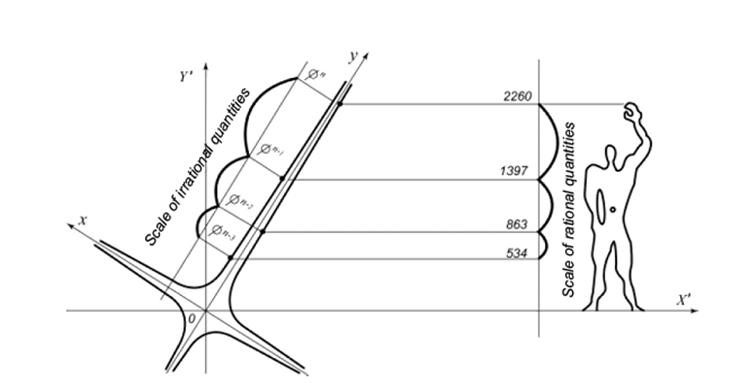
be in some ways linked to the hyperbolic coordinates axes (Fig. 26). The sequence
of irrational relations will be reflected on the axis 0y, the integral-valued
sequences will be created from Y' coordinates by the same series of
points located on the neighboring hyperbole branches through one rotation
module.
Fig.26. Reference
of Modular scales to axes of hyperbolic coordinates. So, what are the common
features of phyllotaxis dynamic symmetry, Modular and Hambidge's dynamic
symmetry? The answer is that in all these cases we deal with the same
mathematical regularities, namely, golden hyperbolic functions. Really, on
Hambidge's scheme (Fig. 2) the base of the arbitrary parallelogram can be
interpreted through the golden sine (Gsh x) and diagonal- through the golden cosine (Gch x).
Then we get the formula of J. Hambidge's invariant of dynamic symmetry: Gch2 x -
Gsh2 x = 1. Of similar interest is
the possibility of Modular numerical regularities interpretation. The numerical
sequences of red and blue scales are considered recurrent (ignoring some
,,small" ambiguities); it means, we can apply to them the formula of constant
(invariable) of phyllotaxis dynamic symmetry: |un2 + un
· un
- 1 - u2
n - 1| = const. Let us determine the
invariant value for the red scale. We take any couple of neighboring numbers,
for example, 6 and 9. We shall get |62 + 6 ·
9 - 92| = 9. Now we shall determine the
invariant for the blue scale. We take numbers 18 and 30:
|182 + 18 ·
30 - 302| = 6. It is necessary to remember that
the formula used in this case reveals
characteristic dependence (12) of
golden hyperbolic trigonometry, discovered by us. The numbers of red and
blue scales can be considered as hyperbolic coordinates X' and Y'
of square lattice vertices (see Fig. 17) that belong to two specific
hyperboles. For one of them a' = const = 9, for the other - a' = const = 6. Our generalization will
be incomplete if we do not remind that features of space-time in special theory
of relativity is also characterized by invariant. Such invariant is the so
called special-temporal interval which value is preserved in the process of transfer from one inertial
system to the other and is expressed in the formula Dt2 - Dx2 = const. Here dependence of hyperbolic trigonometry ch2
x -
sh2 x = const also is the mathematical sub base of this
expression Thus, we have grounds for
the final conclusions. 1. Mathematical research of phyllotaxis described
above establishes the fact that this phenomenon shows regularities of
non-Euclid, to be more specific, pseudo-Euclid geometry more known as
Minkowski's geometry. So far, physics was considered to be the only field where
this geometry was realized. But it was V. E. Vernadskiy who suggested that the
laws of natural pattern formation are based on non-Euclid geometry. [6]. Therefore, our findings can be
considered as those that specify of V. E. Vernadskiy's suggestions. 2. Phyllotaxis geometry and its trigonometric
apparatus reflect peculiarities of mathematics of nature. This is the form of
mathematics where fundamental role belongs to golden section. 3. J. Hambidge's principle of dynamic symmetry, Le
Corbusier's proportional system of Modular, phyllotaxis
dynamic symmetry as well as spatial-temporal invariant of special theory of
relativity have common mathematical grounds of Minkowski's geometry
regularities. Therefore, there are substantial grounds to refer to them as
common regularities of art and nature. |