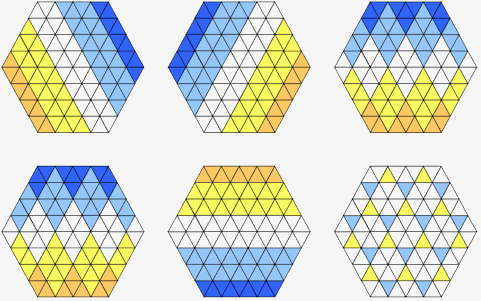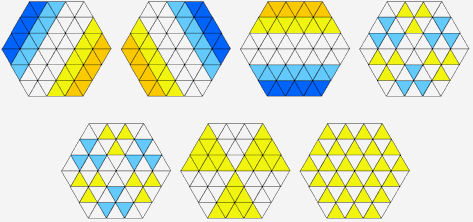|
properties of a hexagon John Baker
and David King
Abstract
We begin with the definition
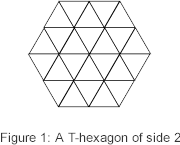
of a T-hexagon of side n. This is a hexagon of side length
n whose interior is divided into equilateral triangles of unit side. For
example, the T-hexagon of side 2 is as shown in Figure 1.
Our interest in the potential of visual schema for analysing the properties began with our exploration of the different ways in which the numbers 1 – 24 can be arranged in this configuration, with one number in each triangle such that the total in each row is the same. Given that the rows are oriented in three directions there are thus 12 constraints on the positioning of the numbers, and when these constraints are met, the resulting configuration is called a magic hexagon, or more fully, a magic T-hexagon of side 2. The outcomes of this investigation are described elsewhere; here we focus on a visual schema that enables some other features of the magic hexagon to be described.
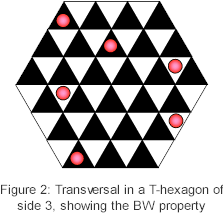
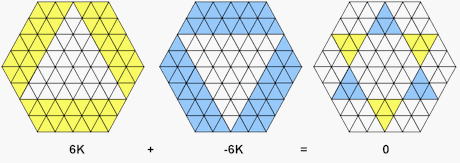
At the same time as investigating the existence and properties of a magic hexagon, we were made aware of a simple property that a transversal of a hexagon appears to possess. A transversal of a hexagon is defined as an arrangement of objects within the triangles of a hexagon with the property that there is exactly one object in every row. If the triangles that make up the hexagon are coloured alternately black and white, then it appears that in every transversal there are the same number of objects in black triangles as there are in white triangles. For example, Figure 2 shows a transversal for a T-hexagon of side 3. Note that three of the objects are in black triangles while 3 are in white triangles. We have called this the BW property. Visual Notation As part of our investigation, we noticed that a magic hexagon appears to have the BW property, in that the numbers that lie in black triangles add to the same total as the numbers in the white triangles, which is half of the total available. For example, in a T-hexagon of side 2, there are 24 numbers distributed between the triangles and their total is given by:
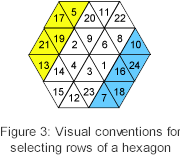
The total of the numbers in the black triangles was found to be 150, and this proved to be the case in all of the many examples of magic T-hexagons that we tested. To understand why this might be happening, we introduced a visual notation in which we represented the fact that we wanted to include the numbers contained in a row of triangles by colouring the triangles in yellow. We also needed a way to express the idea that the numbers selected in one row could be balanced by the numbers in another row, thus we used a second colour, blue, to represent the idea that the numbers in blues cells would be included but in negative form. For example, Figure 3 gives a magic T-hexagon of side 2 which is coloured to express the equation: 13 + 21 + 19 + 18 + 17 + 5 – 7 – 18 – 16 – 24 – 10 = 75 – 75 = 0
We have included the actual numbers in Figure 3, in order to demonstrate the visual convention that rows coloured yellow are considered positive and row coloured blue negative. In what follows, we will leave the numbers out, but the reader should bear in mind that at every stage of a visual argument, the intention is that the values in the triangles are being manipulated. Example of a Visual Proof Whilst conducting the search
for configurations that gave magic hexagons, we made use of the relationship
expressed by the equations of:
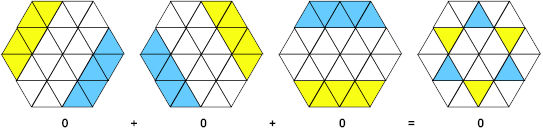
Figure 4: A visual result By overlapping the selected rows, we are able to show that particular triangles can be singled out to become part of an expression. Here, when the middle triangles in each outside row are selected alternately positive and negative, the result is a balance or zero. In terms of the actual numbers used in Figure 3, the result of the generalisation described by Figure 4 would be that: 19 + 8 + 23 – 20 – 16 – 14 = 0 The Visual Method The right-hand diagram of Figure 4 is one that we encountered a number of times. It comes in two forms, one expanded and the other repeated. These are shown in Figure 5.
Figure 5: Extending a result to 2 rows In Figure 5, two rows are
used instead of one, but the pattern of the result is the same as that
for Figure 4. We also added the algebraic confirmation of the result, using
the convention that K stands for the total of a row. In Figure 6, we introduce
a further convention, in which darker shades of a colour are used to show
that the row is counted twice; at the same time, we have dropped the algebraic
labelling and let the pictures speak for themselves.
Figure 6: A more complex visual proof. The pattern of Figure 4 is repeated in tessellating form in Figure 6. Interesting Patterns The result of Figure 6
can also be used in a visual proof of the BW property for the T-hexagon
of side 4. But before going into the proof, we give some of the interesting
patterns that we found for T-hexagons of side 2. These are given
in Figure 7.
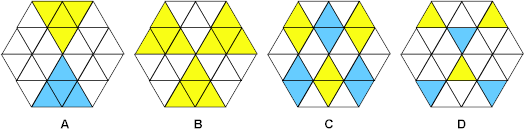
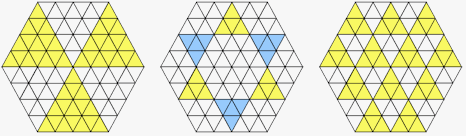
Figure 7: Four patterns that repeat in higher order T-hexagons
Figure 7A Figure 7A represents the
fact that in a magic hexagon, opposing sectors add to the same total. The
orientation of the sectors is not important, thus the same pattern can
be rotated by 60° and by 120° and the result remains true. Figure
7B builds on 7A, and shows that half the total of a magic hexagon is to
be found in three alternate sectors. The chequered pattern of Figure 7C
is made by interweaving four rows, two going in one direction, the other
two going in a different direction. Add the result of Figure 4 to Figure
7C to obtain Figure 7D. Here the same tessellating pattern of Figure 7
appears, only a different part of it is showing from that which shows in
Figure 4. Most importantly, in the light of the BW property, Figure
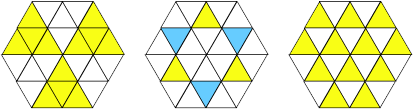
7B can be combined with Figure 4 to give Figure 8:
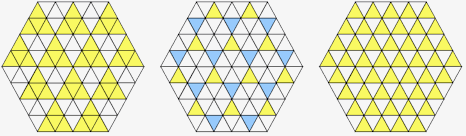
Figure 8: The BW property in a T-hexagon of side 2 Figure 8 gives a visual proof that the BW property holds for T-hexagons of side 2. The patterns of Figure 7 can be generalised to higher order hexagons, in the manner of Figure 5, where two adjacent rows are coloured rather than just one. Thus in Figure 9, we use the result of Figure 5 together with an extension of Figure 7B to obtain the result shown.
Figure 9: Alternating triangles of side 2 The first part of Figure 9 shows half the total of a magic hexagon, this time contained in triangles of side 2. Combining this result with the result of Figure 7, gives the second part; this is a visual proof that the BW property holds for T-hexagons of side 4. Proof that the BW Property holds for all n Using the diagrams that
led to the proofs of the BW property for T-hexagons of sides
2 and 4, we isolated exactly what combination of rows was required to select
the triangles required for the BW property. For the case of the
T-hexagon of side 4, our findings showed that the further the row
is from the centre of the hexagon, the more often it is used. We then found
that the same pattern applied to other sized hexagons, and will illustrate
the process with the T-hexagon of side 3.
Figure 10: A visual proof of the BW property for a T-hexagon of side 3 The form of the visual proof in Figure 10 suggests a general formula that can hold for any value of n. The first three row combinations to be used are found by counting from the main diagonal in each case. The first row is not used. The second row is used once, the third row is used twice, the fourth row is used three times and so on. This happens in each of the three directions. In general, then, the nth row from the diagonal of a T-hexagon will be used n-1 times, and in each of the three directions. The alternate sector diagram is combined with these three configurations to generate a diagram in which only the triangles that point upwards are selected in yellow. In a formal sense, we can make the inductive hypothesis, Hn, that alternate triangles in a T-hexagon of side n are selected by the composition of three hexagons in which the rows are selected in the manner described together with the alternate sector diagram. We have shown that Hn is true when n = 2, 3 and 4. If we suppose that Hn is true for n = k, then the diagram for the T-hexagon of side k + 1 is formed by increasing the size of the alternate sector diagram and adding a row to each side of the other diagrams that is either a blue row of weight -k or a yellow row of weight k. By assuming that Hk is true, we know that the inside T-hexagon will result in alternating triangles. In the top outer row, all the extra yellow triangles are of weight k, and the blue triangles are of weight k, k, k-1, k, k - 1 and so on, ending with two triangles of weight k. Combining these will result in the required alternating pattern. Hence Hn is true for all n. Implications for Magic Hexagons and Transversals We have shown elsewhere [1] that magic configurations only exist for T-hexagons of side 2n. The proof of the BW property holds for all n, and thus applies in particular to all magic hexagons, in which, therefore, the total of the numbers in the 'black' triangles is the same as the total of the numbers in the 'white' triangles. For magic hexagons, the total in each row was shown to be
For the transversal, however, we can replace the object by 1 and assume that all other triangles contain 0. In this case, the row total for every row is 1, and the 1s are therefore positioned such that they have the BW property. That is, half the objects will be found in black triangles and half in white triangles. The meaning of the other configurations represented by Figures 4 – 10 can be interpreted in a similar way. For example, in a transversal, opposite sectors hold the same number of objects (Figure 7A). One final word: As authors of this paper, we have shown only the results of a search for patterns and proofs. We have not included the many pages of trials, errors and reorganisation that led to our final understanding of the BW property and its interpretation for magic hexagons. However, we would like to stress that the visual schema that we developed made a great impact on our ability to see patterns and build on them. Indeed it was very much the visual part of our mathematical activity that enabled us to find these results. References Baker, J. E. and King, D. R, Magic Hexagons (to appear) Baker, J. E. "Hexagonia" from Natural Maths. http://www.naturalmaths.com.au/hexagonia King, D. R. "Hall of Hexagons" from http://www.drking.plus.com/hexagons
|