The Fourier Analysis of Bezier Curves
Paul Barry
Abstract: We use the Discrete Fourier Transform to analyze
Bezier curves.
|
1 Introduction
The Bezier curve is a basic element of many computer graphic
toolsets. This is not surprising, as it is easy to define and has well-understood
mathematical properties. In this article, we apply the Discrete Fourier
Transform to the construction of Bezier curves to gain more insight into
their structure. As a Bezier curve is determined by its control polygon,
this analysis is intimately linked to the Fourier analysis of the control
polygon. An analysis of polygons in the plane has been carried out in [2].
Our work can be seen as a specialization of this.
2 Preliminaries
We let P0, P1,¼,Pn
be n+1 points in the plane. Let t be a parameter, normally an element of
[0,1]. Then the Bezier curved defined by the points P0, P1,¼,Pn
is defined by the vector equation
| P(t) = |
n
å
k = 0 |
Ckn(1-t)ktn-kPi |
|
(1) |
We recall that the polygon determined by the points P0,
P1,¼,Pn is called
the control polygon of the curve. For instance, the line segments P0P1
and Pn-1Pn are tangents to the start, respectively,
the end of the curve.
The above equation results from an iterated process of
subdividing line segments in the ratio t:(1-t), starting with the line
segments PkPk+1, k = 0¼n.
In the case of n = 3, for instance, we have
|
| P(t) = (1-t)3P0+3t(1-t)2P1+3t2P2+t3P3 |
|
| = |
æ
è |
|
|
|
ö
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
| = |
æ
è |
|
|
|
ö
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
| = |
æ
è |
|
|
|
ö
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
(2) |
|
|
|
We recognize in the square matrix the inverse of the 4×4
binomial matrix. This is the matrix with general form
| B = |
æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
whose (j,k)-th element is equal to C(j-1,k-1).
It is instructive to see the effect of
B-1
on the power basis (1,x,x2,¼).
In the 4×4 case, for instance, we have
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
= |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
We now introduce the Discrete Fourier Transform [3]. If we
let f0, f1¼fn
be n+1 numbers, real or complex, then their Discrete Fourier Transform
is the set of n+1 numbers
|
^
f |
j |
= |
n
å
k = 0 |
fke-2pijk/(n+1) |
|
(3) |
where i = [Ö(-1)]. The numbers
[^f]j are in general complex numbers. We can invert this transformation
as follows :
| fk = |
1
n+1 |
|
n
å
j = 0 |
|
^
f |
j |
e2pijk/(n+1) |
|
(4) |
We shall refer to the (n+1)×(n+1) matrix with (j,k)-th
element e-2pijk/(n+1) as the (discrete)
Fourier matrix
F. For instance, in the case n = 3, we have
|
æ
ç
ç
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
ø |
= |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
= |
1
4 |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
3 Analyzing Bezier curves
We now apply the foregoing to Bezier curves in the plane.
We observe that a point P in the plane can be regarded as a complex number,
so that taking the Fourier transform of a set of points makes sense. We
let wj = e-2pij/(n+1)
be a solution of the equation
Then
|
| P(t) = |
n
å
k = 0 |
Ckntk(1-t)n-kPk |
|
| = |
n
å
k = 0 |
Cknti(1-t)n-k |
1
n+1 |
|
n
å
j = 0 |
|
^
P |
j |
wjk |
|
| = |
1
n+1 |
|
n
å
k = 0 |
|
n
å
j = 0 |
Ckntkwjk(1-t)n-k |
^
P |
j |
|
|
| = |
1
n+1 |
|
n
å
j = 0 |
|
^
P |
j |
|
n
å
k = 0 |
Ckn(twj)k
(1-t)n-k |
|
| = |
1
n+1 |
|
n
å
j = 0 |
|
^
P |
j |
((1-t).1+twj)n |
|
(6) |
|
|
|
This exhibits P(t) as a linear combination of ``basic" Bezier
curves, since we have
|
|
|
| = |
n
å
k = 0 |
Ckn tk(1-t)n-kwjk |
|
| = |
n
å
k = 0 |
Ckntk(1-t)n-kwkj |
|
(7) |
|
|
|
Hence
| P(t) = |
1
n+1 |
|
n
å
j = 0 |
|
^
P |
j |
Bj(t) |
|
(8) |
for the Bezier curve with control polygon (P0,P1,¼,Pn).
These basic Bezier curves have control polygons determined
by the numbers {wkj},
and hence the geometry of these curves is determined by the geometry of
the corresponding star-polygons [1].
4 A worked example
We let B be the 4×4 binomial matrix :
| B = |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
Then its inverse is given by
| B-1 = |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
The 4×4 Fourier matrix F is given by
| F = |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
with inverse
| F-1 = |
1
4 |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
= |
1
4 |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
Then (2) says that
|
| P(t) = |
æ
è |
|
|
|
ö
ø |
B-1 |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
| = |
æ
è |
|
|
|
ö
ø |
B-1F-1F |
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
|
| = |
æ
è |
|
|
|
ö
ø |
B-1F-1 |
æ
ç
ç
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
| = |
æ
è |
|
|
|
ö
ø |
|
æ
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
ø |
|
æ
ç
ç
ç
ç
ç
ç
ç
è |
|
|
|
ö
÷
÷
÷
÷
÷
÷
÷
ø |
|
|
(9) |
|
|
|
Hence
|
| 4P(t) = |
^
P0 |
+ |
^
P1 |
(1+t(w1-1))3+ |
^
P2 |
(1+t(w2-1))3+ |
^
P3 |
(1+t(w3-1))3 |
|
| = |
^
P0 |
+ |
^
P1 |
((1-t).1+tw1)3+ |
^
P2 |
((1-t).1+tw2)3+ |
^
P3 |
((1-t).1+tw3)3 |
|
|
|
|
(10) |
Here, we have, for instance
| ((1-t).1+tw1)3
= (1-t)3.1+3(1-t)2tw1+3(1-t)t2w12+t3w13 |
|
(11) |
which is the Bezier curve with the four roots of unity 1,w1,w12,w13
or 1, -i, -1, i as control points. We then have
| P(t) = |
1
4 |
( |
^
P0 |
B0(t)+ |
^
P1 |
B1(t)+ |
^
P2 |
B2(t)+ |
^
P3 |
B3(t)) |
|
(12) |
where
| Bj(t) = ((1-t).1+twj)3
= |
3
å
k |
((1-t)ktn-kwjk |
|
(13) |
with wj = e-2pij/4.
This shows that the Bezier curve P(t) is a ``weighted
average'' of basic Bezier curves. We note that in the above case, the basic
curve B0(t) degenerates to the single point (1,0) in the plane,
while the basic curve B2(t) describes the line-segment from
(1,0) to (-1,0) and back again.
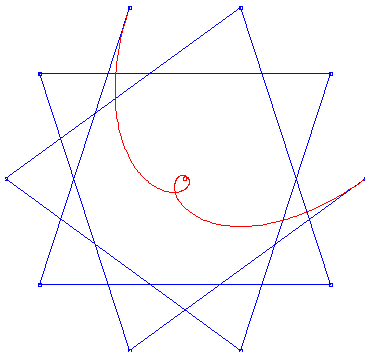
Basic Bezier curve j = 7, n+1 = 10
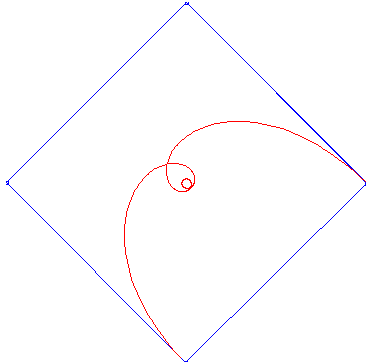
Basic Bezier Curve, j = 3, n+1 = 12
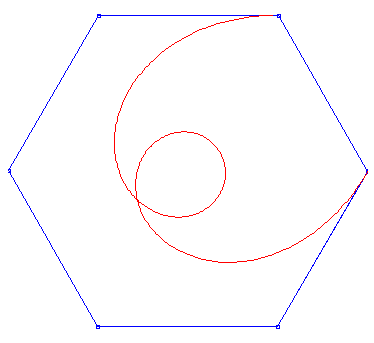
Basic Bezier curve, j = 10, n +1= 12
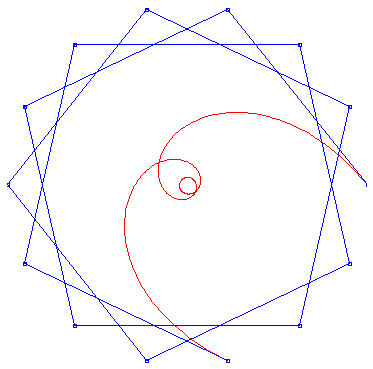
Basic Bezier curve, j = 3, n+1 = 14
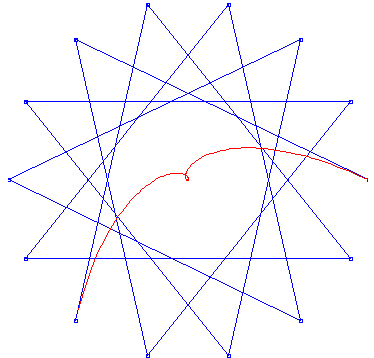
Basic Bezier curve, j = 5, n+1 = 14
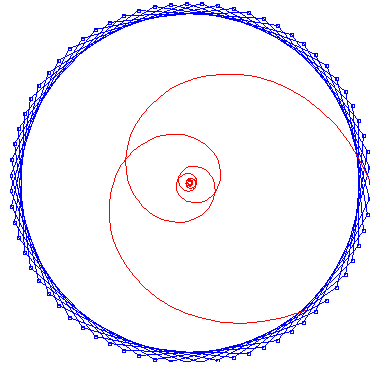
Basic Bezier curve, j = 8, n +1= 71
REFERENCES
1. H.S.M. Coxeter, Introduction to
Geometry (2nd ed.), Wiley, New York, 1969
2. J.C. Fisher, D. Ruoff & J. Shilleto,
Perpendicular Polygons, Amer. Math. Monthly 92 (1985), 23-37
3. E. W. Weisstein, http://mathworld.wolfram.com/DiscreteFourierTransform.html/,2003 |





