|
Introduction
"No two elements interlock, but all three do interlock"
A three-component link with that property is called "Borromean"
after the Borromeos, an Italian family from the Renaissance that used
them as their family crest symbolizing the value of collaboration and unity. 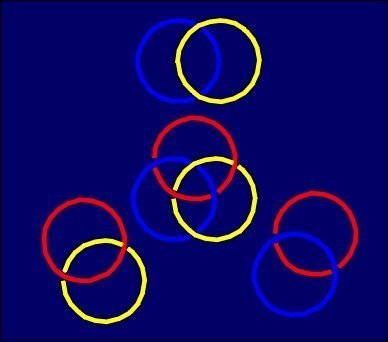
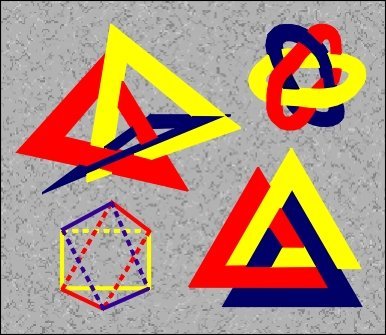
B.Lindström and H.O.Zetterström [1] proved that "Borromean circles are impossible": three flat circles cannot construct them, but by triangles they can. The Australian sculptor J.Robinson assembled three flat hollow triangles to form a structure (called Intuition), topologically equivalent to Borromean rings. Their cardboard model collapses under its own weight, to form a planar pattern. 
P.Cromwel recognized it in a picture-stone from Gotland [2], and it are exactly these and other symmetrical combinations of three and four hollow triangles that were considered by H.S.M.Coxeter [3]. In geometry, Borromean rings appear as the regular octahedron {3,4} [4], in Venn diagrams [5], in DNA [6], and in other various areas [7]. 
|