Some New Tilings of the Sphere with Congruent Triangles
Robert J. MacG. Dawson
Dept. of Mathematics and Computing Science
Saint Mary's University, Halifax, Nova Scotia
Abstract: Many years ago, Sommerville classified the tilings of the sphere with congruent spherical triangles – under some assumptions. Later, Davies did the same, under only the restriction that the triangles should meet edge-to-edge. This paper surveys a recently-discovered class of tilings with congruent spherical triangle tiles that do not meet edge-to-edge.
Introduction. Any simple polyhedron can be "inflated" into a tiling of the sphere with spherical polygons. Perhaps the most familiar example of this is the soccer ball obtained by inflating the truncated icosahedron. If the polyhedron is inscribed in the sphere, then congruent faces give rise to congruent tiles on the sphere. Otherwise, distortion may occur. The triaugmented triangular prism (Johnson solid J51) is an example; inflating it to a sphere must expand some triangular faces more than others.
Not every tiling of the sphere arises from a polyhedron; it is possible that the vertices of a spherical tile may not be coplanar. However, in the special case of triangular tiles, meeting edge to edge, there is a bijection between monohedral tilings of the sphere and inscribed polyhedra with congruent triangular faces. This is one of the various reasons why it was reasonable for Sommerville [5] (in 1923) and Davies [1] (in 1967) to restrict their attention to tiles that met edge-to-edge. Ueno and Agaoka [6], expanding on Davies’ work, did the same. Even under this assumption there are some unexpected and beautiful tilings.
See, for instance, Figure 1. The tiling on the left can be seen as related to the union of an n-gonal antiprism and two pyramids; that on the right is obtained by breaking the other along a skew hexagon, twisting through 120° , and reassembling. They are thus members of an infinite family of tilings. In the case n=5, both reduce to the regular icosahedron. Otherwise, of course, they differ significantly.
Note that neither of these tilings is isohedral; in one case the tiles form two orbits under the symmetry group, in the other there are many orbits. For more information on isohedral tilings, see [7].

Figure 1: Two edge-to-edge tilings with the same tile
This correspondence breaks down if the tiles do not meet edge-to-edge – or at any rate, it gets more complicated. An arc, that is the union of edges in one way on one side and in another way on the other, acts like a degenerate tile with area 0 and angles of 0° and 180° . In the corresponding polyhedron, this becomes a face in the form of a crossed polygon, lying in a plane through the center of the sphere. Such a polyhedron certainly won’t have a single face type.
A little theory. In this section I will give a very brief summary of some of the theoretical ideas that we use in classifying triangles that tile the sphere but not in an edge-to-edge fashion.
(1) Spherical excess. In the Euclidean plane, the angles of a triangle add to 180° . On the surface of a sphere, they add to more than 180° and the amount by which the sum exceeds 180° is the area of the triangle (taking 720° to be the area of the whole sphere.) Thus, for instance, if a triangle has angles 90° , 60° , and 45° , its area as a proportion of the whole sphere is (90° +60° +45° -180° )/720° or 1/48. It follows that a triangle whose excess does not divide 720° cannot tile the sphere!
(2) Vertex vectors. For polygons to tile a sphere, or plane, or any other surface without boundary, they must have at least one way to use each type of angle that they have. This means that each angle must be part of some collection that fit around a point (add to 360° ). For instance, the (102° , 60° ,20° ) triangle cannot tile the sphere, as there is no way to use a 102° angle.
Combinations of angles that do fit at a point correspond to solutions in natural numbers (a,b,c) to the equation aa +bb +cg = 180° . For any triangle, all these "vertex vectors" lie in a plane in the (a,b,c)-space , and the integer solutions can be determined by various methods.
(3) Split vectors. If a triangle is known to tile the plane but not in an edge-to-edge fashion, then there must be at least one vertex that lies on an edge, at which the angles add to 180° . We call such a vertex a split vertex. If such a vertex has a right angles, b b angles, and c g angles, then (2a,2b,2c) is a vertex vector. We call a vertex vector with all components even a split vector.
Except for a few exceptional cases, we can show that more than one angle must be involved in split vectors. One exceptional case is the (90° ,108° ,54° ) triangle (figure 3), which does not tile the sphere edge-to-edge but does tile (in three ways) using no split vertex except for two right angles meeting at an edge [4]. It is also notable for the asymmetry of its tilings; two have symmetry groups of order 2, the third is asymmetric.
(4) The irrationality hypothesis. A little exposure to high school trigonometry should be sufficient to make it plausible that the numbers get messy quickly. To be more precise, angles with rational degree measures usually don’t have rational trigonometric ratios. On the sphere, this leads to the following deliberately vague hypothesis:
"With a few important exceptions, spherical triangles with rational angles don’t have rational relations between their edge lengths."


Figure 2: Spherical and polyhedral versions of a non-edge-to-edge tiling
This is left vague because there doesn’t seem to be a hope of proving it without a major advance in transcendence theory. In the same way, we cannot prove that p is irrational (though most mathematicians would offer excellent odds that it is!) However, as our purpose is to show that certain sums of edge lengths cannot be obtained in more than one way, we just need to know that the edges (A,B,C) of certain specific spherical triangles do not satisfy pA + qB + rC = 0 where p,q,r are integers with absolute value less than, say, 3; and this can be checked very easily (for instance, using a calculator).
For any tiling with N congruent triangles for which this holds, a maximal arc contained in the union of the edges that has p hypotenuses, q long legs, and r short legs on one side of it must have the same number and types of edges on the other side. Summing this over all arcs, we see that the total number 3N of triangle edges, and thus N, must be even. Moreover, if the tiles along such an arc don’t meet edge-to-edge, the most common alternative arrangements have a rotational symmetry (whereas edge-to-edge arrangements often have reflectional symmetry). This explains why (as may be observed) chiral symmetries are the rule among non-edge-to-edge tilings and the exception among edge-to-edge tilings.

Figure 3:
A tiling with the (90°,108°,54°) triangle

Figure 4: Configuration along a great circle arc
(5) Vertex equity. In any tiling by isosceles triangles, there are exactly twice as many base angles as apices; and in any tiling by scalene triangles, there are exactly equal numbers of each kind of angle. However, for some triangles, the possible vertex vectors do not reflect this balance. In particular, there are some triangles for which a certain angle appears more than another in every possible vertex configuration. Such a triangle clearly cannot tile!
We can also make more subtle uses of this principle. If there is only one configuration in which a certain angle appears in at least the target proportion, then that configuration must appear in any tiling. Moreover, if it can be shown – as is often the case – that such a configuration is always accompanied by nearby split vertices with a strong surplus of a different angle, it may still be impossible to create a tiling with vertices in the ratios in which the triangle provides them. In practice, if you try to create such a tiling, you end up with more and more of the hard-to-use species of angle on the boundary, until eventually you get stuck.


Figure 5: Two tilings obtained by group actions
Known tiles. In the remainder of this paper we exhibit various tilings. We believe that these complete the list of isosceles and right-angled triangles that tile the sphere, though the proof of this is rather lengthy. (Some tiles are known to tile in huge numbers of ways; an actual enumeration of tilings, as oposed to tiles, is not expected soon.) Preliminary work suggests that the oblique triangles in the final section complete the list of all triangles that tile the sphere , but at this point this has not been definitely verified.
(1) New tilings with old tiles. Most of the tiles that tile the sphere in an edge-to-edge fashion also tile in other ways. The most common (and least interesting) variation is obtained from an edge-to-edge tiling by way of a "Rubik’s Cube" twist along a great circle. (Fig. 5, left) This is a special continuous case of a usually-discrete process for changing tilings, which often yields non-edge-to-edge results. In general, if the union of some subset of the tiles has a symmetry group G larger than the symmetry group H of the subset, then any element of the quotient group G/H acts nontrivially on the tiling. An example is provided by any of the sets of four tiles filling an octant on the right of Fig. 5.

Figure 6: A swirl tiling with quarterlunes
If a tile will tile a lune with polar angle f , and also some convex polygon P with angles (a 1, a 2, ..., a n) such that f divides (180° -a i) for each i, then there exists a swirl tiling in which P and its mirror image occupy the "polar regions", while the space in between is filled with a swirl of lunes. Many variations on this these are possible! In Figure 6, the lunes, tiled with four tiles each, have polar angle 36° ; two of the tiles make up one triangle of a spherical icosahedron; and the polar polygon is a pentagon with angles of 144°
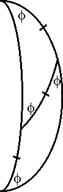
Figure 7: Two isosceles semilunes
(2) Isosceles triangles. In a 2001 paper [3], I classified all the isosceles triangles that tile the sphere. These consist of the known edge-to-edge isosceles tiles found by Sommerville and Davies; three special cases; and an infinite family of semilunes, obtained by dividing the region between two great circles into two isosceles triangles as in Figure 7. This can be done whenever the polar angle f is less than 120° ; when f also divides 360° the triangle tiles. If 360° /f is odd, however, the triangle does not tile edge-to-edge. A tiling of this type is shown in Figure 2.
The three special cases are shown in Figure 8. They are the (80° , 60° , 60° ), (100° , 60° , 60° ), and (150° , 60° , 60° ) triangles, which tile with 36, 18, and 8 copies respectively. The first of these tiles in exactly three distinct ways [2], the second and third uniquely. Note that the (100° , 60° , 60° ) tiling is two-colorable.

(2) Right triangles. Over the course of two summers, I worked with an undergraduate student, Blair Doyle, on a complete classification of the right triangles that tile the sphere. We believe the classification to be complete but are still checking our work on a couple cases.
Every isosceles triangle that tiles the sphere, of course, gives rise by bisection to a right triangle tile. The (90° , 60° , 40° ) tile obtained by bisecting the (80° , 60° , 60° ) triangle tiles the sphere in many ways, none of them edge-to-edge, and might make a nice spherical puzzle!

Figure 9: A design for a puzzle based on the (90°,60°,40°) triangle, which tiles in several ways
There are also a number of other right triangles that tile the sphere. These include the (90°, 60°, 54°) triangle, three of which make up one of the (90° , 108° , 54° ) tiles mentioned above. (The smaller tile was discovered first; my wife, Bridget Thomas, was looking at my sketch and noticed that they fitted together into larger tiles.) It also tiles in several other ways.
Another right-angled tile is the (90° , 72° , 30° ) triangle, 60 copies of which tile the sphere. While both (72° , 72° , 60° ) and (144° , 30° , 30° ) triangles appear in this tiling, neither of them tiles the sphere on its own. The (90° , 105° , 45° ) triangle (on the right of Figure 10), like the tile in Figure 3, is "right-obtuse". The twelve tiles have a delightfully twisty configuration.
The (90° , 75° , 45° ) triangle tiles a 120° lune, three of which tile the sphere (Fig. 11, left). Moreover, by picking the orientations of these lunes properly, two of the three joins may be made edge-to-edge. The only non-edge-to-edge boundaries in this tiling are along the single meridian seen through the transparent front section of this sphere. While in one sense this tile comes extremely close to tiling the entire sphere edge-to-edge, it was easily ruled out by Davies because the (0,3,3) vertex, needed at the poles, could not be realized.




The final right-angled triangle tile, with angles of (90°, 78.75°, 33.75°), was discovered by Mr Doyle, in the last week of our search. It has only one tiling, a structure of great complexity (Fig. 11, right). In particular, the tiling is notable for having a very small symmetry group (order 4) for a tiling with so many (32) tiles. It has 8 different orbits under its symmetry group, a record for the "least symmetric most symmetric" tiling.

(3). Other triangles. There are several other triangles that tile the sphere. The two in Figure 12 are members of infinite families. Both have polar stars joined by a helical equatorial belt of quadrilaterals, but the quadrilaterals divide into triangles differently. The diagonals dividing the quadrilaterals on the left run between obtuse vertices; on the right, they join acute vertices.

The tiling in Figure 13 uses 48 (120° , 45° , 30° ). triangles. It has polar stars like the tilings in Figure 12, but it has a double belt of quadrilaterals around its equator. The complex but symmetric pattern is remniscent of a Fabergé egg. There are not any other closely related tilings with more or less than 12 triangles meeting at the poles. To see this, note that with four different vertex figures, the set of linear equations determining the angles is overdetermined. Thus, in particular, the (3, 0, 0) vertex and the (1, 0, 2) and (0, 4, 0) splits force the (0, 0, 12) polar configuration.
This tiling is also unusual in that all of its triangles are paired into kites. Thus, we also have a non-edge-to-edge tiling of the sphere with 24 congruent (90° , 120° , 60° , 120° ) kites.

Figure 13: The tiling with the (120°,45°,30°) triangle
Acknowledgements. This research was funded by NSERC Canada. The illustrations were mostly done using the excellent and free raytracing package POV-Ray, available from www.povray.org
References
[1] Davies, HL. , Packings of spherical triangles and tetrahedra, Proc. Colloquium on Convexity, Copenhagen 1965, 42-51
[2] Dawson, R., An isosceles triangle that tiles the sphere in exactly three ways, Discrete and Computational Geometry 30 [2003] 459-466
[3] Dawson, R., Tilings of the sphere with isosceles triangles, Discrete and Computational Geometry 30 [2003] 467-487
[4] Dawson, R., Single-split tilings of the sphere with right triangles; in Discrete geometry: In Honor of W. Kuperberg’s 60th Birthday (A. Bezdek, ed.), Dekker 2003
[5] Sommerville, D.M.Y, Division of space by congruent triangles and tetrahedra, Proc. Roy. Soc. Edinburgh 43 (1923) 85-116
[6] Ueno, Y, and Agaoka, Y., Classification of the Tilings of the 2-Dimensional Sphere by Congruent Triangles, Technical Report 85, Division of Mathematics and Information Sciences, Hiroshima University, 2001
[7] Grünbaum, B., and Shepherd, G.S., "Spherical Tilings with Transitivity Properties", The Geometric Vein, eds. C. Davis, B. Grünbaum, and F. A. Scherk, The Coxeter Festschrift, Springer-Verlag, 1981, 65-98