Two and Three-Dimensional Art Inspired by Polynomiography
Bahman Kalantari
Department of Computer Science
Rutgers University
Hill Canter
New Brunswick, NJ, 08903, USA
E-mail: kalantari@cs.rutgers.edu
Abstract
In several previous articles I have described polynomiography as the art and science of visualization in approximation of zeros of complex polynomials. Polynomiography amounts to a colorful two-dimensional image, called a polynomiograph, created via a prototype polynomiography software that could typically allow a great deal of human creativity and control. In this article I describe several types of 2D and 3D artwork that could be inspired by polynomiography. These include work of art as paintings, tapestry designs, carpet designs, animations, sculptures, neon light-like polynomiographs, and more. The realization of some of these applications as serious work of art takes coordinated effort, collaborations, and support. I will report on progress in the realization of some of the above-mentioned artwork.
1. Basic 2D Polynomiography
-
Introduction.
Polynomiography has been defined to be "the art and science of visualization in approximation of zeros of complex polynomials." An individual image is a "polynomiograph." These images are obtained using a variety of algorithms for root-finding, based on the application of iteration functions. The creation of a single polynomiograph is based either on the individual use of an iteration function, or the collective use of a family of iteration function and its point-wise convergence properties. It is not the intention of this article to give any detailed mathematical description of these techniques here. For the mathematical description of polynomiography, see [3], [5], [7]-[9], [11], and [12]. To be able to carry out serious polynomiography one ideally needs to have a good software implementation of the techniques as well as a manual or a book that would describe some rendering techniques. The preparation of these are among the list of projects currently being undertaken. But I would like to make it clear to the reader that just as in photography a great deal of creation lies on the part of the individual polynomiographer. And that is what makes polynomiography a new medium for art, as well as a medium for education and for scientific explorations.
Polynomiography can give many images of the same polynomial. This is analogous to photography where one can shoot many pictures of the same subject. As an example the images in Figure 1 are all polynomiographs of the polynomial equation describing the cube-roots of unity, viewed within a particular square. The only image possibly familiar to the reader is the very first which has appeared quite frequently in the literature describing fractals. A polynomiograph however may or may not turn out to be a fractal image. Here I have limited the number of different polynomiographs of this equation to five, but it is possible to give many many more fractal and non-fractal polynomiographs of this single polynomial equation having very different shapes or colors.





Figure 1: Five different polynomiographs of roots of unity
Polynomiography applies to a general complex polynomial. A polynomial equation can be described via its coefficients:
![]() ,
,
or its complete set of roots as:
![]() .
.
There are advantages in each of these two modes of description. Traditionally a polynomial is described through its coefficient set. But the intention of polynomiography is not just the computation of the roots, rather how the roots are being computed and the effect of this computation in the coloring of the points within a certain domain of the complex plane. This coloring is determined via the use of iteration functions, see [8], and [12]. One of the features of polynomiography is the reversal of the root-finding problem altogether, i.e. given the roots of the polynomial we may ask what iteration function to employ in order to create a pleasing or desired image. This in particular allows the artist or designer working with a polynomiography software the ability to select the location of the roots as he/she wishes.
In the subsequent section I will consider several different applications of polynomiography.
2. Artwork Inspired by Polynomiography
In this section I will describe several applications of polynomiography in creating 2D and 3D artwork. These include, creating paintings, carpet designs, tapestry designs, animations, polynomiography of two or more variables, neon light-like polynomiography, and more. The section also provides some images of the realization of these artwork. These merely show the wide scope of polynomiography and is not intended to be exhaustive.
2.1. Paintings Inspired by Polynomiography
One of the great aspects of polynomiography images and in contrast to most computer-generated art, is in producing images that could resemble a hand-painted artwork. As an example one of my images that has been repeatedly exhibited is the piece I call "Summer," see [6]. This and its variations have inspired me to experiment with real paint and canvas. But I mention that this aspect of polynomiography, i.e. creating actual paintings based on the images is what a number of professional artists have suggested. Thus it is a worthy effort to pursue further. For example the polynomiograph in Figure 2 is an image that inspires hand-painted artwork. I have numerous images like this and in fact one of the features of polynomiography software is that the polynomiographer can experiment with such images before he/she begins to paint one.

Figure 2: A polynomiograph that could be turned into a painting
2.2. Carpet Designs Inspired by Polynomiography
It is possible to create patterns based on polynomiography lending themselves to elegant carpet designs. For instance by using 36 points selected as the roots of a polynomial on three concentric circles I made a polynomiograph which was in fact inspired by an actual Persian carpet design. In turn I had this design turned into an intricate hand-woven carpet having about 1,400,000 knots which took more than 6 months to make. The carpet was produced by one of the finest carpet makers in Iran, Alinasab, whose workshop for carpet making is well-known in the country. Figures 3 shows the carpet in the making and the final artwork, an exact replica of the polynomiograph.


Figure 3: A hand-woven carpet based on a polynomiograph
A second carpet-maker produced the carpet in Figure 4. The design corresponds to a polynomiograph of the same underlying polynomial that gave the first carpet. The difference in coloring and design is due to different use of iteration functions done intentionally to create the contrast between the two designs.

Figure 4: A carpet based on the same polynomial for carpet in Fig 3
2.3. Tapestry Inspired by Polynomiography
Polynomiography could also provide a great source for producing tapestry. As an example a polynomiograph I call "Acrobats," Figure 5, was the basis for the tapestry of Figure 6 made by an artist, Mrs. Azam Barakhshan.

Figure 5: A polynomiograph called "Acrobats."

Figure 6: Realization of Acrobats as tapestry
Lillian Schwartz, one of the pioneers of digital art made it evident to me that viewing polynomiographs under 3D chromatic glasses could often reveal an interesting three-dimensional structure. She thus proposed that some polynomiographs could give rise to 3D sculptures. As an example the image that inspired the carpet of Figure 3 could conceivably be turned into a three-dimensional intricate sculpture. In this sense polynomiography provides an alternative means for mathematically inspired sculptors. Traditionally the field of topology has provided a major source for these sculptors, see e.g. [1], [2], [13]. For instance, M
Öbius bands have been turned into sculptures numerous times. But there is good reason to believe that polynomiography could result in another rich and alternative source for serious mathematically inspired sculptors.
2.5. Animations Inspired by Polynomiography
Animation with polynomiography is a useful technique both in the context of education and art. For instance in [10] we generated some animations that use visualization through polynomiography as a means for conveying certain mathematical concepts. This application could be quite wide in its scope. This is in the sense that polynomiography animations could be helpful to students of various level as well as for highly advanced visualizations that may attempt to capture or discover a deep mathematical property. As an example the following gives a visualization of in the phenomenon known as sensitivity. It is well known that the roots of polynomials could be sensitive to small changes in their coefficients. Classical example is the polynomial
![]() .
.
The coefficient of the sixth power of z is –28. Even if we change this to –28.002 the roots will change drastically and in fact some of them become complex. The following sequence of images can show the gradual change of roots. For the animation of this as well as other animations see [10] and my web site
www.polynomiography.com
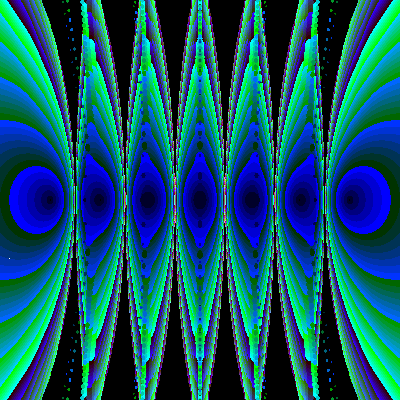
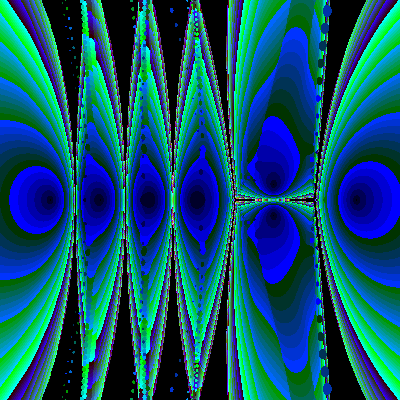
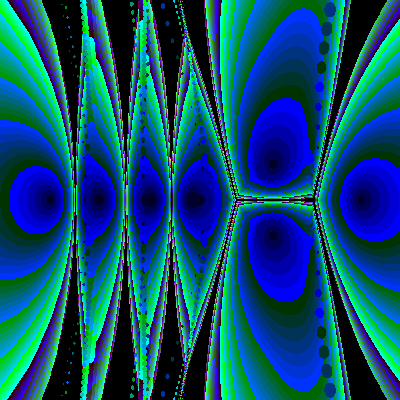

Figure 7: Animation of sensitivity effect.
2.6. Polynomiography of Polynomials in two or more variables.
Polynomiography deals with the visualization of complex polynomials in one variable. But we can still carry out polynomiography on polynomials in two or more variables. Consider for instance a polynomial in two complex variables ![]() and
and ![]() . For each fixed value of
. For each fixed value of ![]() we get a polynomial in one variable and we can generate a polynomiograph. This in a sense amounts to a cross-sectional polynomiography. By repeating this for a range of values of
we get a polynomial in one variable and we can generate a polynomiograph. This in a sense amounts to a cross-sectional polynomiography. By repeating this for a range of values of ![]() , we get more and more cross sections. These cross sections then can be viewed in the form of animation or as a discrete set of images. This too can be a source of for creating animations as art.
Figure 8 gives such a cross-sectional polynomiography for the polynomial
, we get more and more cross sections. These cross sections then can be viewed in the form of animation or as a discrete set of images. This too can be a source of for creating animations as art.
Figure 8 gives such a cross-sectional polynomiography for the polynomial
![]()
![]()

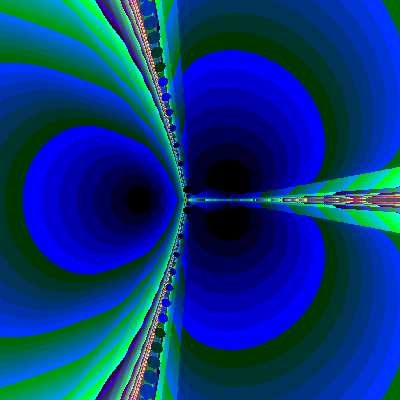


Figure 8: Polynomiography of cross section for y=1,1/2,-1/2,-1
2.7. Neon Light-Like Images Inspired by Polynomiography
Artistically speaking, polynomiography has much to offer. Here I will exhibit a few polynomiographs first produced via a prototype polynomiography software, subsequently subjected to various filters available on existing commercial software to produce new neon-like effects. These filters could have directly been implemented within a polynomiography software itself. These images, see Figures 9, accentuate certain paths that get colored by the polynomiography software based on the degree of proximity of points to polynomial roots, as dictated by the family of iteration functions used in the software. These images suggest neon light-like designs. If actually realized as such they could be quite appealing.
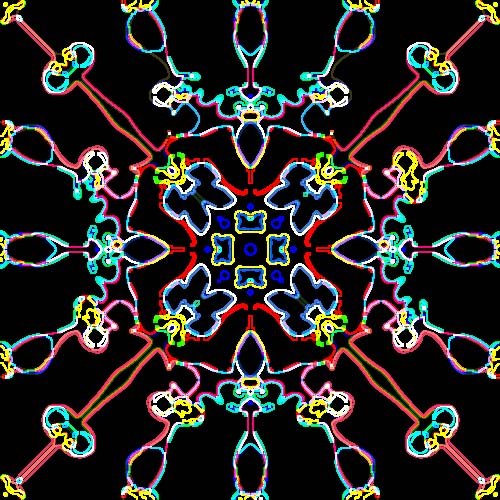

Figure 9: Neon Light-Like Polynomiographs
3. Concluding Remarks and Future Work
In this article I have described several different 2D and 3D applications of polynomiography. These support the proposition that polynomiography represents an excellent medium with diverse applications in art, science and education. The successful implementation and realization of some of the projects into serious work of art or science will however depend upon coordinated effort, collaboration, and support. But probably as evident some of these artwork are already worthy of exhibition.
A referee of this article considered the list of polynomiography-inspired artwork as a "wish list." Moreover, he appeared to object to the fabrication of the two carpets by someone else. These are both very ironic coming from an art-math referee. Firstly, I do not see anything wrong with someone else using my designs in order to produce a beautiful carpet or tapestry. I did not intend to take credit for their artistry. Secondly, it is absolutely true that it is my wish and desire that others will be inspired by polynomiography. Indeed it has already inspired many and I see nothing wrong with that either! The referee also objected that no new mathematics was offered in the article. I did not think it was necessary to discuss the detailed mathematics of the subject here. On the one hand, it really takes a whole book and a software to describe all the details. On the other hand, I do already have several articles on the general mathematical aspects of polynomiography, containing new mathematics that I am very much proud of. Polynomiography is indeed an innovative work that embodies both art and science. As the referee noted I have already used some of the same polynomiographs in published articles. I see nothing wrong with this either. The point of this article is to convey new ideas, rather than new polynomiography artwork of which I have hundreds. There is no need to bombard the reader with variety of images, rather with variety of ideas. In particular the animation, which the referee feel out of place, is yet a new application of polynomiography offering new possibilities as art or as science, although some animation may have been witnessed before, say in chaos (as mentioned by the referee). There are literally hundreds of mathematical ideas that can be conveyed through polynomiography of which the article mentions a couple. And that application, inspired by polynomiography, is a new idea in itself.
This article also serves as an invitation to other artists to create new artwork inspired by polynomiography. It is "my wishful desire" that my polynomiography artwork are transformed into new art forms. Clearly this particular referee and I have very different views. In my opinion art-math societies must strive to make the practice well-defined among their participants, and also try to be inviting, not just to those who practice art-math themselves, but possibly to all who may exclusively practice art or math, students and otherwise.
Acknowledgements. I would like to thank a friend, Mr. Edward Greenblat, an excellent photographer who kindly took the photographs of the two carpets given in this article.
References
[1] C.P. Bruter, Mathematics and Art: Mathematical Visualization in Art and Education, Springer-Verlag, 2002.
[2] M. Emmer, The Visual Mind: Art and Mathematics, MIT Press, 1993.
[3] B. Kalantari, Polynomiography: The art and mathematics in visualization of polynomials, in Proceedings of ISAMA (International Society of Art, Mathematics, and Architecture), 2002.
[4] B. Kalantari, Can Polynomiography be Useful in Computational Geometry?, DIMACS Workshop on Computational Geometry, New Brunswick, NJ, November, 2002.(http//dimacs.rutgers.edu/Workshop/CompGeom/abstracts/005.pdf).
[5] B. Kalantari, Polynomiography and Applications in Art, Education, and Science, in Proceedings of SIGGRAPH 2003 on Education.
[6] B. Kalantari, Summer, artwork and its description in Electronic Art and Animation Catalog, pp. 87, SIGGRAPH 2003.
[7] B. Kalantari, The Art in Polynomiography of Special Polynomials, in Proceedings of ISAMA/BRIDGES Conference, pp. 173-180, 2003.
[8] B. Kalantari , Polynomiography and application in art, education, and science, Computers & Graphics, 28, pp. 417-430. 2004.
[9] B. Kalantari, A new medium for visual art: Polynomiography, Computer Graphics Quarterly, 38, pp. 22-24. 2004.
[10] B. Kalantari, I. Kalantari, F. Andreev, Animation of mathematical concepts using polynomiography, Proceedings of SIGGRAPH 2004 on Education.
[11] B. Kalantari, Polynomiography in art and design, Mathematics & Design, Vol. 4, pp. 305-311. 2004. Proceedings of Fourth International Conference of Mathematics & Design.
[12] B. Kalantari, Polynomiography: From the Fundamental Theorem of Algebra to Art, to appear in LEONARDO, Volume 38. 2005.
[13] I. Peterson, Fragments of Infinity, A Kaleidoscope of Math and Art , Wiley, 2001.