Fermatís Spiral Mandalas
Robert J. Krawczyk
College of Architecture, Illinois Institute of Technology
3360 South State Street, Chicago, IL, 60616 USA
E-mail: krawczyk@iit.edu
Abstract
This paper explores Fermat's Spiral as a method to create circular point figures. It traces previous research into the variety of patterns created by the Fermat's Spiral based on a variety different angle intervals and number of points that control the scale of the figure and the packing of the spiral. Finally, a procedure of combining a series of spirals is proposed to form a mandala.
1. Introduction
Point patterns are an interesting method to represent a variety of mathematical figures. Since they are capable of displaying properties of surface, direction, and line without being any of those, literally, the viewer connects the dots. Two such example is Crova's Disk, Figure 1a., developed from the description developed by Bob Brill [1] from his E Language manual, and 1b. images of strange attractors by Robert Krawczyk [2].

a. b.
Figure 1:
Crova's Disk and a Strange AttractorIn an initial review of possible figures to pursue, Robert Dixon's [3] section on spirals and their representation as a series of polygons demonstrated some interesting patterns. One of the spirals Dixon included was Fermat's spiral; defined by polar coordinates r=k√a, where r is the radial distance, a is the angle from the zero-degree line, and k determines how tightly wound is the spiral; in our case k will be set to 1. Dixon introduced an angular interval d called the divergence, which he computed as 360/c. For example, Figure 2a. displays a spiral where c=360, d=1; the spiral is drawn through 10 turns; 10(360) points. Dixon used this spiral to place polygons along it; in some drawings they were the same size and in others they were adjusted in size as their radial distance increased. Dixon determined that a divergence of 360/
τ or 222.5 degrees results in a true daisy; Figure 2b.; where the polygons are almost equally spaced. He observed that plants in the real world, daises, sunflowers, pineapples, and pinecones demonstrate this pattern. It arises naturally as a space-spacing method of placing seeds.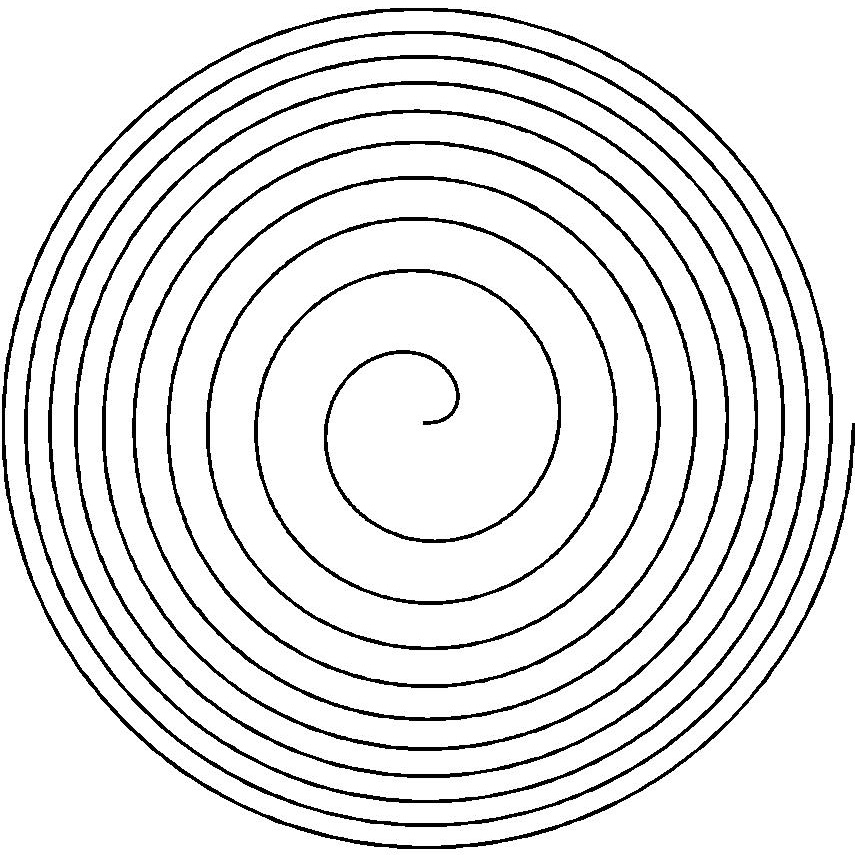

a. b.
Figure 2:
Fermat's Spiral and a True Daisy2. Number of Seeds and Scale
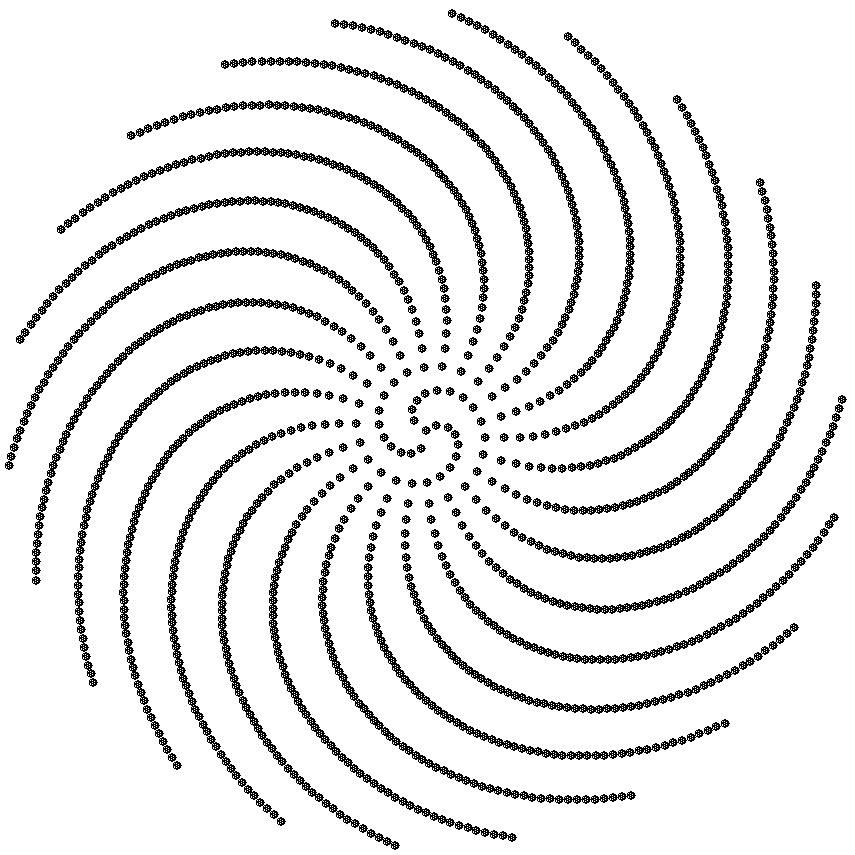
Dixon's placement of polygons or seeds along a spiral results in a pattern similar to the one in Crova's Disk. If the spiral in Figure 3a. is redrawn with seeds with a divergence of 5 degrees placing 2(360) seeds; we see a clear spiral forming at the center and radial lines extending to the edges, Figure 3a. We see a similar effect in Figure 3b. when the number of seeds is increased to 4(360).


a. b.
Figure 3:
Seeds along Fermat's SpiralThe effect of scale, increasing the number of seeds but keeping the outer radius the same, begins to introduce other patterns. In Figure 3a., we see spirals in two directions, as well as, radial lines. Dixon experimented with other values for c, such as,
π, √2, and e, and noted secondary spirals forming; some winding clockwise and others counterclockwise. Figure 4 displays two such spirals with 4(360) seeds based on π, 114.6 and √2, 254.6 degrees.

a. b.
Figure 4:
Spirals based on c equals π and √2More recently Michael Naylor [4] also approached the placement of seeds when he investigated the same mathematical relationship as Dixon but with different divergence values so that seeds would not be arranged along radial lines. He was able to determine the number of seeds that would result in a specific number of turns so a seed would return to the starting zero-degree line. Naylor also noted that the increase in the number of seeds would create a variety of spirals and radial lines within the larger pattern.


a. b.
Figure 5:
Naylorís p flowersFor example; in his p Flower, the angle of divergence is 50.97 degrees; computed as p 360, or p revolutions, reduced to 0.14159 or 50.97 degrees. Figure 5a. displays the p Flower at 2(360) seeds and Figure 5b. 4(360) seeds. Naylor further investigated why 7 spirals were generated and the relationship of the seeds that fell on the zero-degree line with Fibonacci numbers. Figure 6 displays a √2 Flower, 1.41421(360), or 1.41421 revolutions, reduced to 0.41421 or 149.2 degrees. This particular value generates a series of clockwise and counterclockwise spirals as Dixon had noted and also distributes the seeds equally. Naylor also included the Golden Flower, 1.618(360) or 222.5 degrees which had the same equally spaced seeds as Dixon had found. Naylor continued his investigation by connected the seeds with lines and then determining the number sequences formed.

Figure 6: Naylorís √2 Flower
3. A Geometric Mandala
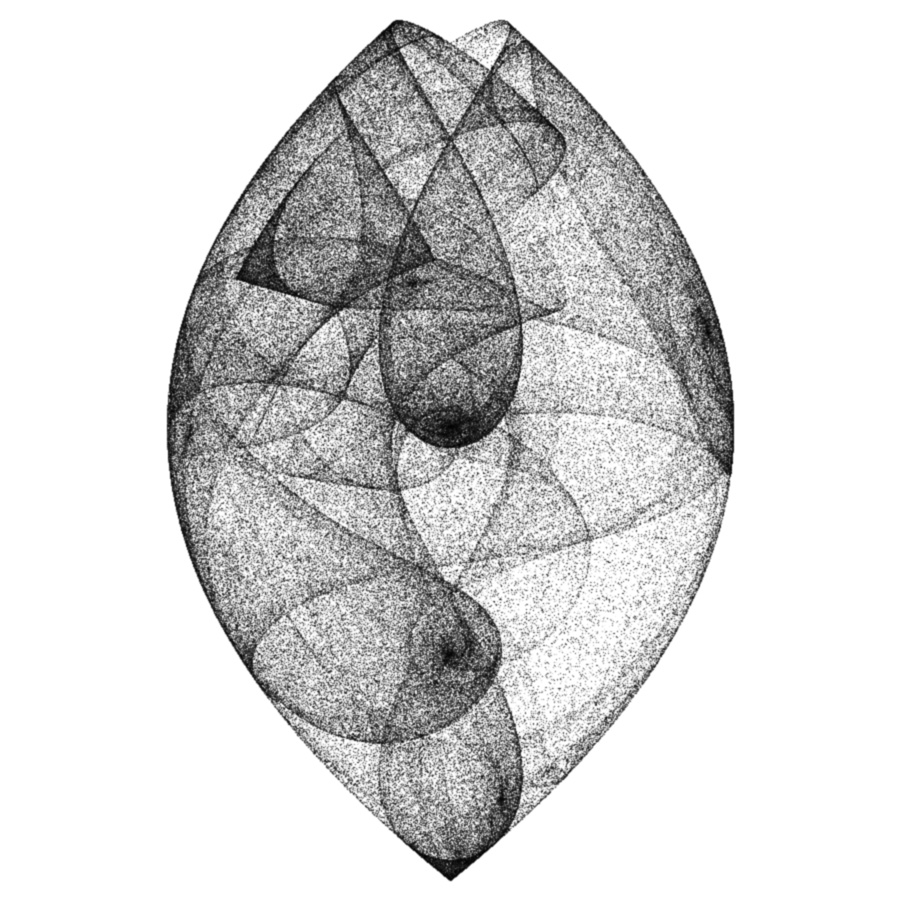
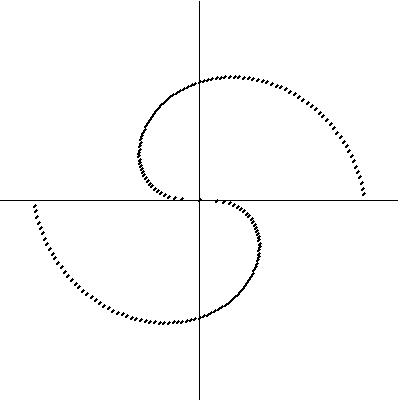
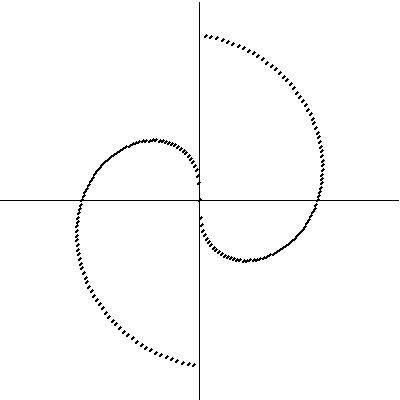
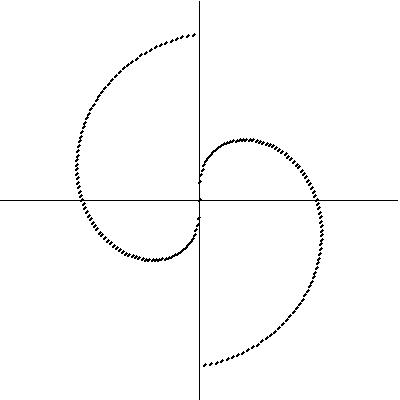
Since Fermatís Spiral exhibited this interesting property of the placement of seeds and generating a variety of spiral and line patterns, a compositional procedure was investigated to repeat the spiral within a circular form, a geometric mandala. Figure 7a. displays the original spiral with at 0 and 180 degrees with a counterclockwise angle interval; Figure 7b. at 0 and 180 degrees clockwise; Figures 7c. and 7d. are the same as 7a. and 7b. but rotated 90 degrees counterclockwise. Figure 8a. displays the first four spirals combined; 8b. the last four spirals, and finally, 8c. all the spirals.
a. b. c. d.
Figure 7:
Individual spirals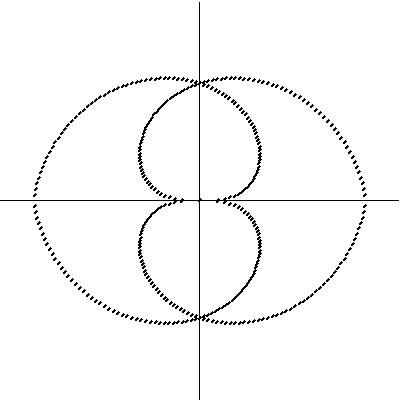
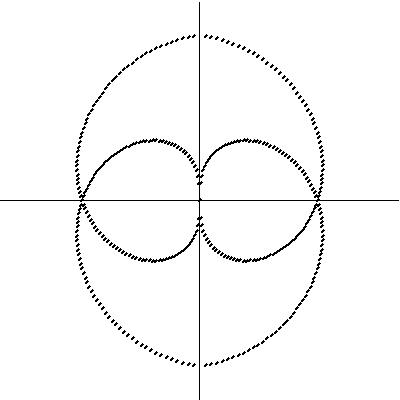
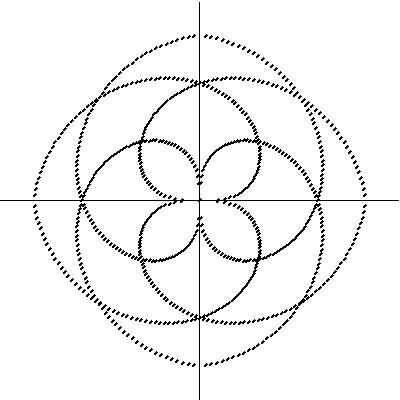
a. b. c.
Figure 8:
Combination of spiralsThe relationship to mandalas is based on the circular form these figures take on, using the simple geometric definition of "mandala"; from the Sanskrit for circle. A mandala is a complex circular design, intended to draw the eye inward to its center having symmetrical and radial balance. The Fermat's Spiral in particular is a natural basis for this inward draw.
Using the spiral formed by Naylor's √2 Flower as in Figure 6, Figure 9a. displays the combining of the first two spirals; 9b. the first four spirals; and 9c. all 8 spirals combined.



a. b. c.
Figure 9:
Naylor's √2 Flower Mandala



Figure 10:
Examples of Fermat's Spiral MandalasFigure 10 displays a series of mandalas based on some of the spirals suggested by Dixon. They include √2, 254.6 degrees; e, 132.5 degrees; plus variations: e/2, 264.9 degrees, and e/4, 169.8 degrees. As the original spirals demonstrated interesting patterns of inner spirals and lines, the combined version also beginning to exhibit patterns that included: rays, pedals, zig-zags, squiggles, hexagons, swirls, and spirals in all directions and length. The generation and initial inspection of some 900 mandalas shown a large number of such combinations of elements; some congregating around the center, some along the edges, and some in between. Also noted was that a minor change of only 0.1 degree would generate a much different pattern. Currently, no attempt has been made to understand the mathematical relationship between the angle of divergence and the patterns generated.
Figure 11 displays Naylor's √2 Flower at 149.2 degrees. To further enhance the texture of the mandala, the black and white image generated by the combination of the 8 spirals was passed through a Bas Relief filter. The final version is rendered with a copper finish. More examples of such mandalas can be found at: http://www.home.netcom.com/~bitart

Figure 11
: Naylor's √2 Flower Mandala as a Bas Relief print
References
[1] Brill, Bob, 2001, Algorithmic Imagery Using E, Zenagraf, p. 125
[2] Krawczyk, Robert, "Dimension of Time in Strange Attractors", in ISAMA and Bridges 2003 Joint 2003 Conference, edited by R. Sarhangi
[3] Dixon, Robert, 1987, Mathographcis, Dover Publications, Inc., pp. 126-138
] Naylor, Michael, ďGolden, √2, and π Flowers: A Spiral StoryĒ, in Mathematics Magazine, June 2002, pp.163-172