|
PERIODIC SPONGE SURFACES AND UNIFORM SPONGE POLYHEDRA IN NATURE AND IN THE REALM OF THE THEORETICALLY IMAGINABLE By Michael Burt- Prof emeritus, Technion, I.I.T. Haifa Israel
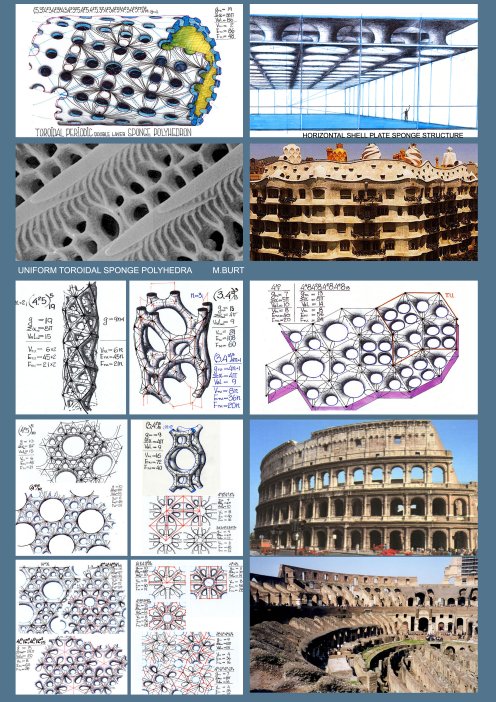
Introduction The diversity of shapes and forms which meets the eye is overwhelming. They shape our environment: physical, mental, intellectual. Theirs is a dynamic milieu; time induced transformation, flowing with the change of light, with the relative movement to the eye, with physical and biological transformation and the evolutionary development of the perceiving mind ."Our study of natural form "the essence of morphology", is part of that wider science of form which deals with the forms assumed by nature under all aspects and conditions, and in a still wider sense, with forms which are theoretically imaginable…..(On Growth and Form – D'Arcy Thompson), "Theoretically" to imply that we are dealing with causal- rational forms. "It is the business of logic to invent purely artificial structures of elements and relations. Sometimes one of these structures is close enough to a real situation to be allowed to represent it. And then, because the logic is so tightly drawn, we gain insight into the reality which was previously withheld from us" (C. Alexander). A particular interest should be focused on those structures which are shaped like solids or containers, with continuous two-manifold enveloping surfaces, enclosing a volume of space and thus subdividing the entire space into two complementary sub-spaces, sometimes referred to as interior and exterior, although telling which is which, is a relativistic notion. On each of these envelopes, topologically speaking, an infinite number of different maps composed of polygonal regions (faces), which are bounded by sets of edge segments and vertices, could be drawn, to represent what we call polyhedra, or polyhedral envelopes. We come to know them by various names and notations, evolving through many historical cultures up to our present times; each representing an individual figure-polyhedron, or a family, a group, a class or a domain; convex-finite, Platonic and Archimedean polyhedra; pyramids, prisms; anti-prisms; star polyhedra; deltahedra; zonohedra; saddle polyhedra, dihedral, polydigonal, toroidal, sponge like, finite and infinite polyhedra; regular, uniform, quasi-regular, and so forth; all inscribable in our 3-dimensional space. It is these structures and their extended derivatives which shape our physical-natural or artificial man-conceived environment and provide for our mental pictures of its architecture. The number of forms which had acquired a name or a specific notation through the ages is amounting to infinity, although the number of those which comprise our day to day formal vocabulary and design imagery is extremely (and regretfully) limited by comparison, even amongst designers and architects, whose profession, by definition, compels them to manipulate and articulate forms and space. Here it is right to observe that name-giving is part of the creative and generative process. The number of polyhedral forms which did not receive, as yet a proper name or a notation is also infinite. Infinite is also the number of potentially existing and possible imaginary periodic forms, not envisaged yet. Conspicuous are those relating to sponge-like labyrinthian, polyhedral, space dividing surfaces, which until quite recently were not even considered as a research topic. The interest in these forms has been prompted by our growing awareness of their abundance in nature and their importance, not only in describing micro and macro-physical and biological phenomena, but also in coping with morphological complexity and nature of our built environment and its emerging new architecture and the order and formal character of our living spaces, on either the building or the urban scale. Nature is saturated with sponge structures on every possible scale of physical-biological reality. The term was first adopted in biology: "Sponge: any member of the phylum Porifera, sessile aquatic animals, with single cavity in the body, with numerous pores. The fibrous skeleton of such an animal, remarkable for its power of sucking up water". (Wordsworth dictionary). Of course the term applied to 'spherical sponges'. It turns out that the key characteristic of porosity is attributable to a much wider morphological phenomenon. With time the expressions: sponge, spongy, sponginess, spongeous', were adopted in many languages to describe a physical phenomenon which is characterized by porosity and visual permeability and the condition of a lump of matter which, as a result of biological-chemical-physical processes of erosion-corrosion, growth and death, acquired its characteristic porosity. Numerous examples in the surrounding nature, on the microscopic and the macroscopic scale, carry a testimony to the abundance of the phenomenon: microscopic radiolarya bones, eroded rocks and gigantic cave labyrinths. Slowly but steadily we are becoming aware that the sponge phenomenon is basic and dominant on the nano-scale of the big protein molecules and according to Stephen Hanking, also on the macro-cosmic (black-holes) scale. "The outer space of the cosmos lost its Euclidean rectiliniarity to the hyperbolic curvature of Riemannian geometry"….(William Day)- --1989). It transpires that the phenomenon is the most abundant in the physical and the organic material world of nature. With some extrapolation of the perceiving mind it is right to claim that the sponge phenomenon, with its porosity and permeability characteristics, is central to the physical morphological nature of the human habitat, and represents its defining imagery. Historically speaking, the phenomenon was received with great consternation. It was associated in the human mind of its time with extreme, unresolved complexity. The labyrinth of Knossos became the mythological archetype of a complex phenomenon, beyond the capacity of any descriptive discipline, geometric-mathematical or even literary-verbal. Of course it is beyond the reach of Euclidean geometry. The labyrinth myth came to represent impotence of the human intellect in face of a bewildering, puzzling complexity.
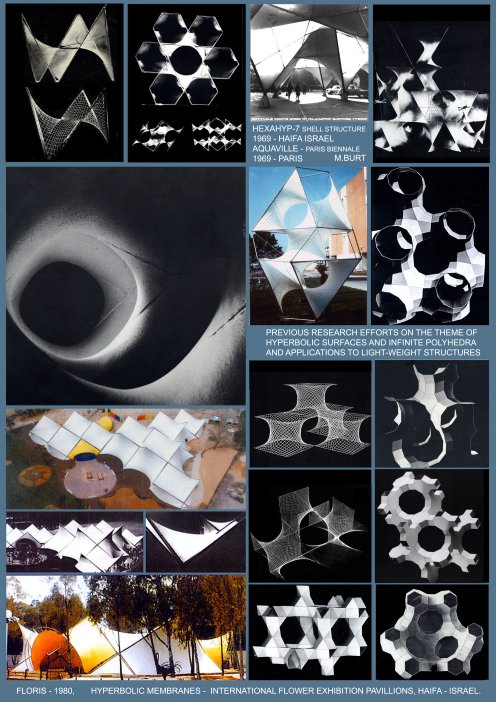
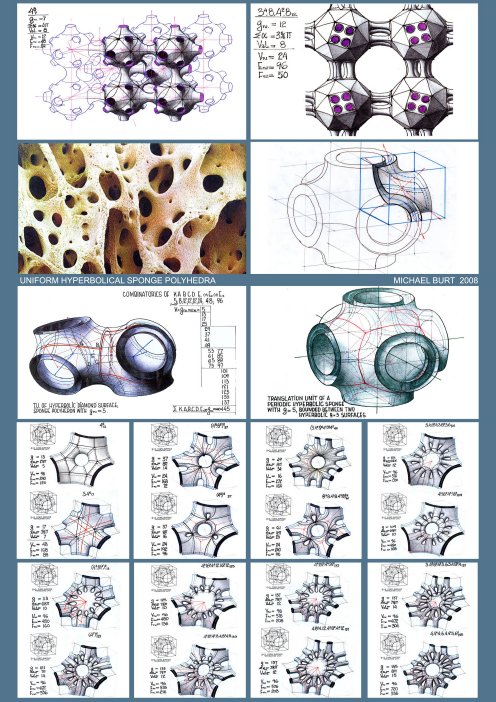
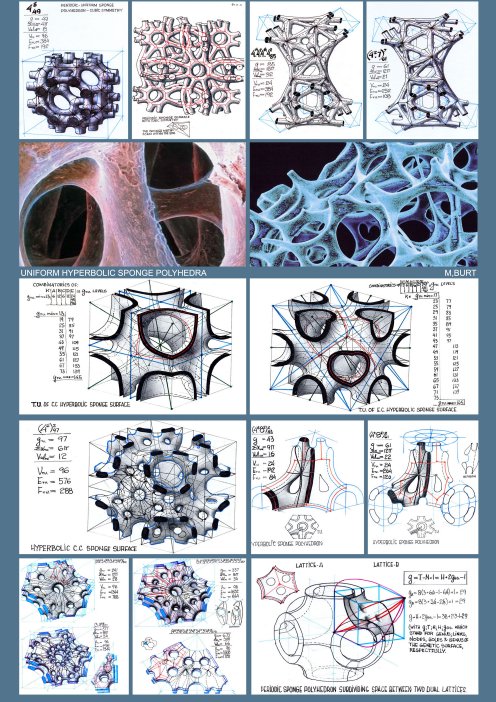
Generation of Sponge SurfacesSponge Polyhedra are mosaic maps drawn on a sponge surface, which means that the later has to be generated first. three main conceptual methods were devised for generation of sponge surfaces.
Considering any two complementary (dual, reciprocal) continuous space lattices and constructing the spatial partition surface, subdividing space between the two. If the two complementary space lattices are periodic in character, corresponding to a specific space symmetry group, its symmetry characteristics will be shared by the resulting sponge surface. If the two complementary lattices are identical (self-dual), the resulting sponge surface may subdivide space into two identical sub-spaces, with each of the lattices acting as it's Tunnel Space Lattice (T.S.L). The number of possible such sponge surfaces is corresponding to the number of dual lattice pairs and therefore any exhaustive search of such surfaces and complementary lattice pairs is one and the same problem. It seems that the number of such topologically different space subdividing sponge surfaces is reaching to infinity (Identical Dual Lattices and Subdivision of Space – by Ami Korren, 2003). Considering any continuous, unbounded base surface (A) which, when duplicated so as to produce two parallel surfaces, thus describing a 'double skin' volumetric feature, and if perforated so as to leave the surface continuous and unpunctured (unbounded), results in a sponge surface. The (A) base surface may be referred to as the 'Genetic Surface' (Ge.S) of the sponge envelope. The resulting sponge surface shares with the Genetic surface its symmetry characteristics. Due to inherent complexity of the subject, the authors efforts to develop a uniform sponge polyhedra embedded in a 'Quatric' Sponge Surface, were so far frustrated. Multi-layer Sponge surfaces When Ge.S. is replicated in a parallel mode and the associated double skins perforated, and when the resulting adjacent sponge sheets are joined together by surface sleeves, the resulting feature may be aptly described as a multi-layer sponge surface, and the number of layers corresponds to the number of parallel Ge.S.s. It transpires that the number of layers may reach to infinity. Generation of Uniform Sponge Polyhedra As previously stressed, the number of topologically different sponge surfaces is infinite and even more so the number of sponge polyhedra. Throughout history, only few tried to approach rigorously the ordering problem of the polyhedral array of forms in its totality. One was Rene Descartes who in the first half of the 17-th century, while referring to convex regular polyhedra, stated that: The total angular deficit, of the sum of the angular deficits, take n over all the vertices of a convex polyhedron, equals 4π for (all) regular polyhedra.
Another giant, observing the field while standing on the shoulders of Descartes, was Leonard Euler, the founder of topology, who stated in the so-called Euler's Theorem: "The number V-E+F=K, (V, E, F stand for vertices, Edges and Faces, respectively, with K, called the characteristic of the manifold), is the same for all permissible maps on the manifold." In general, Descartes' and Euler's theorems could be presented as follows: Definitions Generally speaking, any far-reaching definition of polyhedra is admissible as long as it does not violate Euler's formula of: V-E+F=2(1-g).
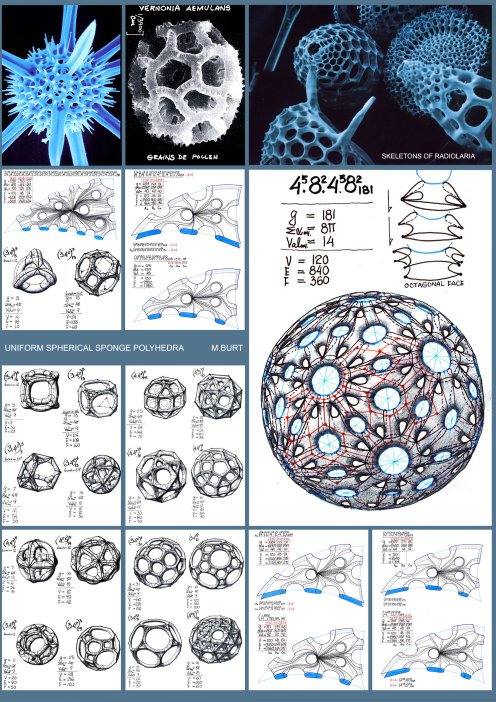
Polyhedral map drawing on a sponge surface must lead to polygonal faces which may constitute, under a suitable topological transformation, a plane polygonal region. Uniform Polyhedron is a polyhedron with the same repeating vertex figure and the same cyclic order of polygonal faces about each of its vertices. The Primary Parameters of the Polyhedral Universe. The parameters found to be most suitable to describe the polyhedral phenomenology in 3-D space are the following:
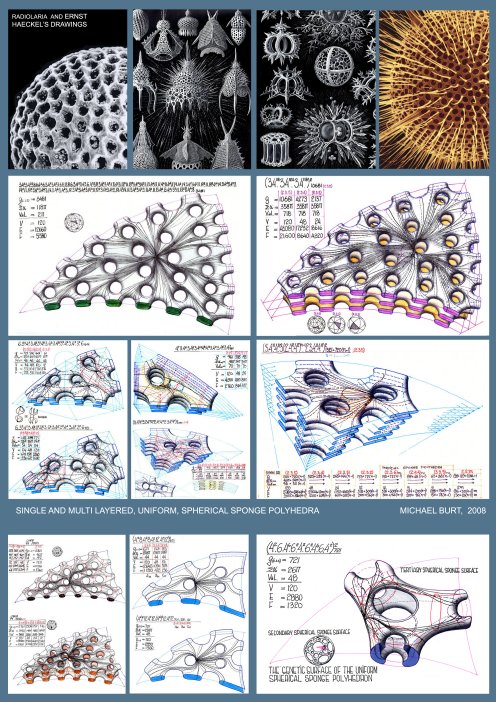
For all sponge-like polyhedral maps, drawn on sponge surfaces, g≥2 (with the resulting values for K as negative, even and natural numbers). The genus-g of the sponge polyhedron's 2-d manifold (in 3-D space), which subdivides between two complementary Tunnel Space Lattices A&B, each with LA.&LB. lines (axes) and NA.&NB. Nodes, respectively, is: g=LA-NA+1=LB-NB+1, and if periodic and infinite in extent, the polyhedron's geometry and its g-value may be represented by its Translation Unit (TU.).thus: g(TU.)=LA(TU.)-NA(TU.)+1=LB(TU.)-NB(TU.)+1 ∑αav.=2π(1-2(1-g) ) V ∑α could be derived from the polyhedron's notation, by adding all the polygonal angles in a vertex, as if the polygonal faces are planar and regular,. In the case of a non uniform polyhedron, the calculated ∑α value (on the basis of g& V) should refer to its average value (∑αav.). It was revealed after a prolonged exploratory process that any meaningful collection of polyhedra, if arranged according to the growing valency values, show a consistent evolution of (most of) their secondary parameters (V, E, F, average polygon-Pav., stability, and so on). Generally speaking, Val. Represents density of the polyhedral lattice and has a critical bearing on stability of the lattice, when realized as a physical bar & joint space frame. It could be derived from the following relations: Pav.F=2E=V.Valav. where Pav, F, E&V stand for average Polygons, Faces, Edges and Vertices, respectively. Generation of 'Uniform Sponge Polyhedra' Generation of Uniform Sponge Polyhedra must adhere to some geometrical-topological constraints and the a.m. definitions, to ensure non-self-intersection, continuity of the polygonal mosaic and full conformity with the Euler's theorem. Uniformity of the vertex configuration requires adherence to specific symmetry groups of the sponge surface and the structure of its defining complementary tunnel-lattice pair. It is self-evident that any Elementary Periodic Region (E.P.R) or Elementary Periodic Surface Region (E.P.S.R) must contain one and only one vertex (and vertex figure). Applying successfully these constraints and generating a 'proper polyhedron, with its full notation, comprising the cyclic order of the polygon types and the genus value suffix, we can establish all the parameters, primary and secondary, which are necessary to describe and account for the Polyhedral feature. The results must stand the test of the established mathematical relations and conform with the previously stated theorems. Hierarchical Order and Classification of the Periodic Sponge Surfaces and the 'Uniform Sponge Polyhedra' Domain The search disclosed an infinite array of Sponge Surfaces and Uniform Sponge Polyhedra. The employed exploratory process involved a certain fusion of symmetry and topological reasoning and combinatorics.
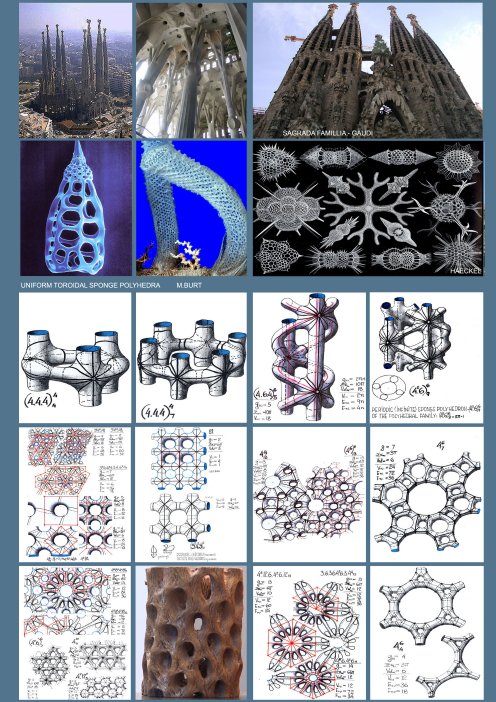
symmetry groups, represent a genetic clan of sponge surfaces and Any Ge.S. can be replicated in a parallel mode, to result in multilayered sponge surfaces and polyhedra. The resulting n-layered sponge surfaces and polyhedra, where n can reach to infinity, and with their g, ∑α& Val. values, as functions of the number n, raise considerably the attainable complexity of the polyhedral sponge configurations. The number of all g-levels of all the genetically related sponge surfaces, derived from one and the same primary Ge.S, and their corresponding sponge polyhedra are deducible from symmetry related perforation combinatorics and their layered structure. In conclusion, the hierarchical order of Periodic Sponge polyhedra is revealed through the following feature levels:Phenotypes -a morphological-topological categorization into: Primitive; Spherical; Toroidal & Hyperbolic Periodic Sponge Surfaces. Symmetry group -classification of the a.m. Phenotypes according to Symmetry Group characteristics. Ge.S-types -classification according to Tunnel Lattice Systems and related Genetic Surfaces (Ge.S) and their genealogy. Strata-Count -classification according to the number of Ge.S layers. Perforation mode-classification according to the mode and extent of Perforation Polyhedral Family- all sponge polyhedra, sharing same phenotype, symmetry-group, Ge.S, number of Ge.S. layers and same mode of perforations. Additional classification, down the hierarchical ladder, is following a path of increasing polyhedral regularity level, starting with polyhedral mosaics which utilize curved edge segments and curved face-polygons, and gravitating toward polyhedra with straight and identical edge-segments and regular and identical plane face polygons and identical dihedral angles with (463; 643; 663), as the most regular (Coxeter) Sponge Polyhedra.
The Periodic Table of the Polyhedral Universe. In view of the extent and complexity of the polyhedral domain, with all its diversity and its infinite number of members and their apparent groupings into families and phenotypes, according to various topological and symmetrical characteristics and the nature of their morphological behavior, it is only natural, as complex as it seems, to look for a general framework which can accommodate and account for them all. One of the most effective ways to present a multi-parametral phenomenon in comprehensive (and visual) terms is to plant it into a coordinated space, with some of its most meaningful and fundamental (primary) parameters as its coordinates. The most celebrated example is, of course Mendeleyev's 'Periodic Table of the Elements' (1869), in which, as a result of an extensive correlation of the properties and the atomic weights of the elements, with special attention to valency (representing the atomic bonding), he proposed the periodic law, by which "the elements arranged according to the magnitude of atomic weights show a periodic change of properties". The 'Periodic Table of the Elements provided a 2- dimensional coordinated space in which every element has a unique point representation. Historically speaking, the evolving location patterns of the elements have promoted deep insights into the structure and order, governing this domain, and permitted to make successful predictions about potential elements, on the basis of their location and neighborhood characteristics. Of course, the key to a successful table is in the right choice of its parameters- coordinates, and the establishment of coherent mathematical relations between these parameters and as many of the others as feasible, suitably embracing all the important properties, capable of describing the polyhedral nature. The 'Periodic Table of the Polyhedral Universe' (its name) is, to some extent a visual animation of Euler's formula of V-E+F = 2(1-g), producing a medium through which all its apparent and hidden meanings are revealed. The 'Table' is constructed on the basis of thoroughly selected primary parameters, of Valav., ∑α av. and g, which seem to capture the essence of the polyhedral- topological nature, and when used as coordinates of a Cartesian 3-D space, provide for an environment in which every conceivable 3-D polyhedron has a unique point representation. It goes without saying, that due to space combinatorics and permutations, the same parameters of Val, ∑α & g might be shared by more than one polyhedron, thus giving rise to the notion of 'isotopes'; i.e. polyhedra sharing same location within the 'Table's' space.The 'Table' is bridging over the g-domain borders of spherical (g=o) polyhedra, the Toroidal (g=1) and the hyperbolic (g≥2) sponge like polyhedra and brings the whole polyhedral universe into a unified perspective. All conceivable polyhedral phenomena of topological association and similarity relationships, between various polyhedral groups, phenotypes and families, describable in terms of the primary parameters, support location patterns, on the basis of which a comprehensive classification and hierarchical structure of the entire polyhedral universe can be constructed. These location patterns, some of which are universal (namely embracing all the polyhedral universe), and some of which are limited, local, unique or esoteric, describe by proxy, polyhedral properties of varying significance and scope, and their relative distribution within the coordinated and highly structured space. What is visually (and intellectually) striking is the realization that while all the accumulated rich imagery of finite-spherical and the toroidal polyhedral mosaics are limited to g=o & g-1 domains and ∑α= - 2π χ 2π; the sponge polyhedral imagery stretches over all g- domains (g≥2), with g, ∑α & Val. values reaching to infinity. THE EXTENT OF THE UNIFORM SPONGE POLYHEDRA DOMAIN, WITHIN THE POLYHEDRAL UNIVERSE When perceived through the coordinated space of the 'Periodic table of the Polyhedral Universe', it becomes clear that with the addition of the recently developed Sponge Polyhedra, the emerging polyhedral universe is exploding to cosmic proportions, as compared with the 'Ptolemaic world picture' of the polyhedral domain of just one decade ago. When all the horizon of sponge structures is taken in, it dawns on us that the number of periodic sponge surfaces with all their phenotypes, symmetries, layered arrangements and modes of perforations and polyhedral families many of which include infinite number of members, each, is overwhelming; much in excess of all the familiar polyhedra in the g = 0 (spherical) and the g = 1 (toroidal) domains. So, its not just in the natural-physical-biological, but also in the abstract realm of the theoretically imaginable world of geometry that the sponge configurations and imagery constitute an overwhelmingly greater majority of shapes and forms, and it is high time to inaugurate their exploration within and by the morphological community, to compensate for millennia long neglect of the subject .Attached is a visual-pictorial evolution of the 'Sponge imagery', relating to Periodic sponge Surfaces and Uniform Sponge Polyhedra and associated images in nature and man-made architecture. Natural forms illustrations of radiolarya, pollen seeds, bone structures, plant patterns, some of considerable magnification, were taken from various internet sources, published literature and private collections. All surface and polyhedral graphic realizations are the author's free hand drawings. All Space Structures, realized and conceptual, are part of the author's day dreaming projects. References
Publication (Faculty of Architecture and Town Planning) Israel, 139 pp.
|