|
BIFURCATIONS AND ATTRACTORS IN BOGDANOV MAP
Ilhem Djellit, Ibtissem Boukemara
Abstract: In this paper, we study bifurcation space and the phase plane of the Bogdanov map. Specific bifurcation structures can be observed in parameter space, related for instance to embedded boxes structure and configurations of bifurcation curves of periodic points near the cusp. This model is a diffeomorphism. The dynamics is extremely rich, involving periodicity, quasi-periodicity and chaos. The method of the study is a numerical iteration to an attractor in which the guesses are inspired by the theory. Bifurcation diagrams obtained in different parameter planes are given and a sketch showing the cusp bifurcations, for the versal unfolding of Bogdanov map, is given. Phase plane is also studied, different attractors are shown, their evolution giving rise to chaotic attractors is explained. Basins of attraction are considered and fuzzy boundaries of basins are put in evidence. The study of such kind of diffeomorphisms can give an interesting contribution to nonlinear systems. Key words: bifurcation, basin, Bogdanov map, invertible, chaos. Classification: 34D45-37D10-34C37
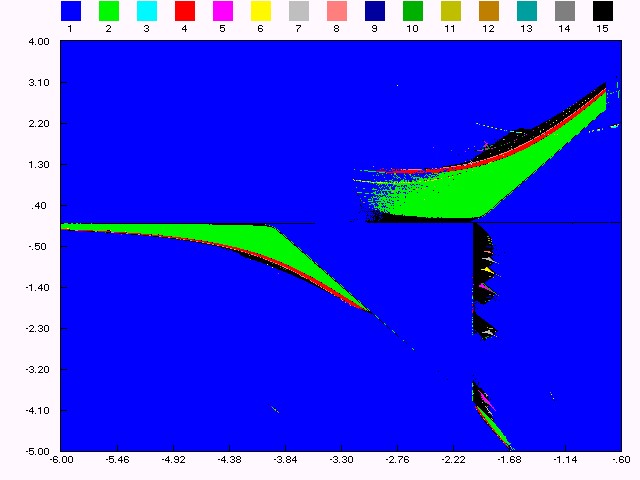
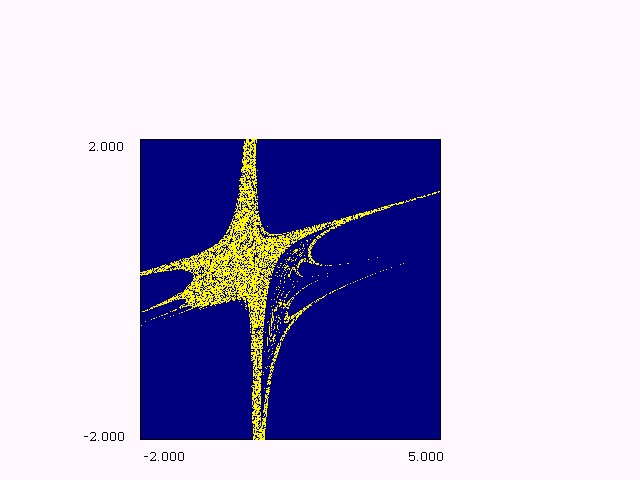
Introduction We study a diffeomorphism. The dynamics involves various transitions by bifurcations. A planar quadratic map which is conjugate to the Hénon map in its conservative limit (see [H1]). Perturbation theory here reveals periodicity and quasi-periodicity, parametrically organized by embedded boxes structure. Outside these parameter regimes the perturbation becomes larger and bifurcations complicate the dynamics, often involving chaos. On the one hand, this concerns local bifurcations, e.g. cascades of flips and cusp bifurcations. On the other hand, we have to deal with homoclinic bifurcations. It also undergoes a Hopf bifurcation which creates a stable closed curve growing out, at its destruction appears a saddle connection. Here the dynamical features are explored by numerical methods. Also, we often iterate to a periodic attractor. In several cases we find interesting dynamical objects predicted by the theory and global phenomena in the parameter plane. This kind of scanning has been made for giving a first idea about bifurcation organization. That is, the dynamic behaviors may be, as expected, regular (equilibrium , stable cycles and stable invariant curves) or chaotic. Object of the present study is to investigate the main routes to complex behaviors in attracting sets and their basins of attraction associated with the dynamics of invertible nonlinear systems which are still of great interest. The Bogdanov map provides a good approximation to the dynamics of the Poincaré map of periodically forced oscillators, first considered by Bogdanov (see [B1]), Takens and Arnold [A3] in their study of the double zero eigenvalue singularity, they proved the existence of a codimension-two fixed point at the origin, called a Bogdanov-Takens cusp with a nonzero Jordan canonical form but the best contribution come from Arrowsmith and al. [A1, A2]. We emphasize that our aim is to study simply the map without emulate the Bogdanov vector field. This diffeomorphism can be considered as a model giving rise to a complete set of bifurcations with a fractal structure, and with birth of cyclic invariant curves (impossible to obtain with Hénon map). From this point of view it gives the fundamental mechanisms occurring in the non-autonomous differential equation with quasi periodic solutions, or more complex solutions. The considered diffeomorphism is the following termed by Bogdanov map: T: xn+1 = xn+yn+1, yn+1 = yn+eyn+hxn(xn-1)+mxn.yn (1) Where x, y are real variables, e, m are real parameters . The parameter h is the step length in the discretization, it takes small values. T has not a constant jacobian determinant J = 1+e+mx, then it results from this situation that a cycle can undergo the Hopf bifurcation and for e = m = 0, we observe the hamiltonian nature and we have a globally area preserving map. Eq. (1) has only two fixed points (0,0) and (1,0). These both fixed points can undergo identical sets of bifurcations in parameter space, this is due to the symmetry in the map (see Fig.1 (a,b,c)) under the transformation ([`x] ,[`y]) = (1-x,-y) which switches the fixed points. We study the bifurcation diagram which consists to show
bifurcation curves in the parameter (e,h),(e,m)
planes together with representative phase portraits. The Figures 1 (a,b,c)
give the parameter value for which at least one fixed point is attractive
(blue domain corresponding to the value 1). More generally, the Figures
1 (a,b,c) give the regions of parameter ( e,h)
or (e,m) plane for
which at least a periodic orbit of order k exists (k = 1,2,...,14).
Each part coloured corresponds to the existence of a periodic orbit of
order k (period) of which is given by the upper coloured squares.
The black regions (k = 15) corresponds to the existence of bounded
iterated sequences.
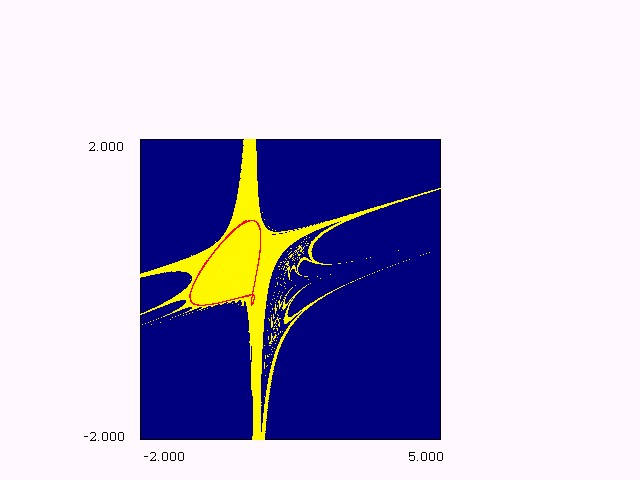
Figure (1.a): bifurcation
structure in (
eh) plane, m
= 2.
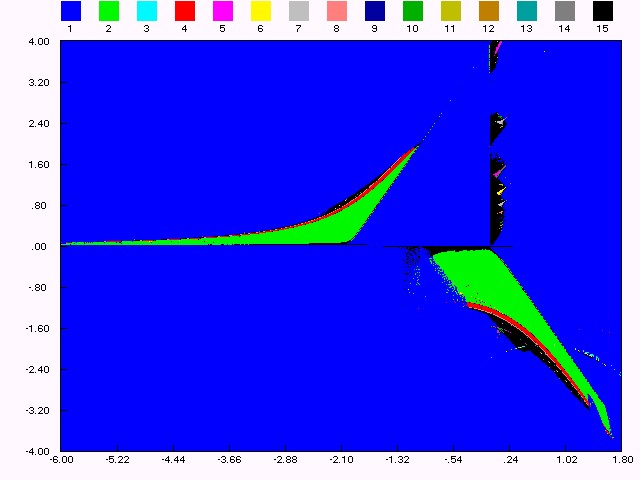
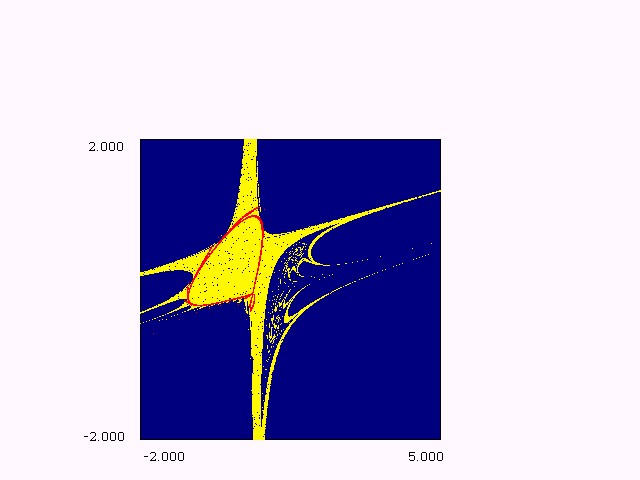
Figure (1.b): bifurcation structure in ( e,h) plane, m = -2. These figures are typical of maps with dominating quadratic
nonlinear terms, analogous bifurcation diagrams have already been obtained
for systems with non linearity given by hyperbolic tangency [M1,
M2,
T]. We can recognize on the diagram period doubling bifurcation,
saddle area and spring area [M1]. The bifurcation structure
is a quadratic "box-within-a-box" type (see [M3,
F2]),
as is well known infinitely many periodic are opened by fold bifurcations
and are closed by homoclinic bifurcations by the intriguing "box-within-a-box"
bifurcation structure. There is a fold bifurcation on the line h
= 0, a flip bifurcation on the line
e = h/2-2,
and a Hopf bifurcation on the line e = 0 for
0 < h < 4.
The eigenvalues of the fixed point at the origin depend on the parameters
(e,h), in the interior of the curve e2+h2-2eh-4h
= 0 we have complex eigenvalues.
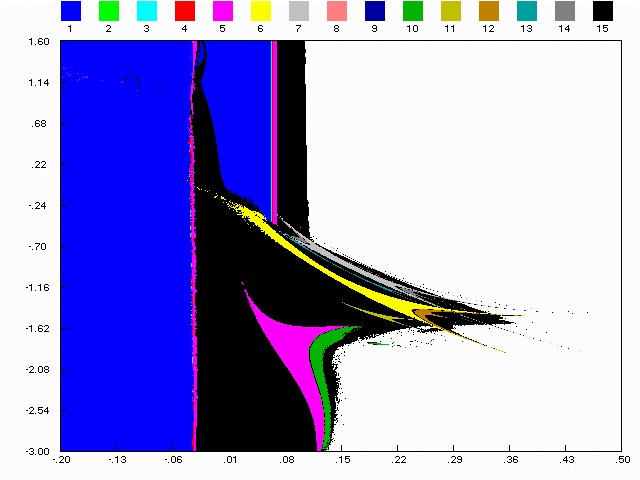
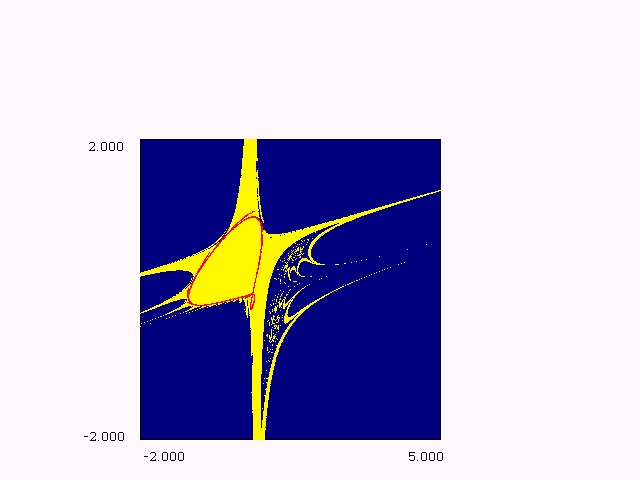
Figure (1.c): bifurcation structure in (e,m) plane, h = 1.44.
Definitions and some properties This section essentially concerns a two-dimensional map T , considered here as a discrete dynamical system in R2 (xn+1, yn+1) = T (xn, yn) = (f (xn, yn, l), g (xn, yn, l)) where f (x, y, l) and g (x, y, l) are continuous and differentiable functions with respect to real variables x, y and continuous with respect to the real parameter l. It is recalled that a closed and invariant set A is called an attracting set if some neighborhood U of A may exist such that T(U) ÌU, and Tn(x, y) ® A as n®¥, "(x, y) Î U. An attracting set A may contain one or several attractors coexisting with sets of repulsive points ( strange repulsors) to either chaotic transients towards these attractors, or fuzzy boundaries of their basin [M4]. The set D = Èn³ 0T -n(U) is called the total basin (or influence domain) of A. That is, D is the open set of points x whose forward trajectories (set of images of x) converge towards A. D is invariant under backward iteration T-1 of T, but not necessarily invariant by T: T -1(D) = D, T (D) ÍD. The relations above hold also for the closure D of D. The boundary of D is denoted by ¶D, is defined by the geometrical equality ¶D = D Ç[`C(D)], where C(D) denotes the complementary set of D. This boundary satisfies : T -1(¶D) = ¶D, T (¶D) Í ¶D. The basin D may be connected or non-connected. A connected basin may be simply connected or multiply connected (which means connected with holes). An attracting set is called periodic of period k if it is made up of k disjoint sets, A = Èi = 1kAi, where each Ai is an attracting set of the map Tk. When A is an attracting set of period k = 1 , then its total basin is given by D = D0 if it is connected, by D = Èn³ 0T -n(D0) if it is non-connected. When A is an attracting set of period k, the immediate basin D0 of A is the open set D0 = Èi = 1nD0, i , the D0,i being open disjoints basins of Ai. If A is connected attractor , the immediate basin D0 of A is defined as the widest connected component of D containing A. When A is the widest attracting set of a map T , its basin D is the total basin of bounded iterates. That is, the open set D contains A such that D is the locus of points of the plane having bounded trajectories. Definition 2.1: A chaotic area A is an invariant absorbing area (T(A) = A)), the points of which give rise to iterated sequences having the property of sensitivity to initial conditions. About chaotic areas, it is important to emphasize that the study of such area has only the purpose to obtain properties giving rise to fractal basin boundaries. Definition 2.2: We say that l = l* is a bifurcation of contact of A , if a contact between the frontier of A and the frontier its basin of attraction takes place. Proposition 2.1: When a bifurcation of contact of a chaotic area A arises for a value l = l*, the crossing of this value leads to the destruction of A, either to a qualitative modification of properties of A (i.e. a sudden and important modification of the size of such an area or its basin of attraction). The destruction of A, after the crossing of the bifurcation value has been demonstrated by Gumowski & Mira [GM]. The qualitative change of properties of A has been described by Mira & al. [M4]. Definition 2.3: Let S be a saddle fixed point of T; a q point is called homocline to S, so q Î Ws(S)ÇWu(S) and q ¹ S. q is a transversal homocline point, so Ws(S) intersects transversally Wu(S). We say the basin boundary is fractal if it contains a transversal homoclinic point. Definition 2.4: One calls homoclinic orbit Oo(q) associated with q, q belonging to a U(S) of S, a set constituted of successive iterates of q, and its infinite sequence of preimages obtained by application of the local inverse map T l-1of T in U(S). Definition 2.5: Let T be a diffeomorphism of IR2 depending on a parameter l and let S be a saddle point of T. A homoclinic bifurcation takes place, if for a value l = l*, there is apparition (or disappearance) of an infinity of homoclinic orbits. Overlapping of global stable and unstable manifolds usually
leads to nonlocal bifurcations. The existence of a transversal point of
a planar map leads to very complicated behavior of orbits nearby. Such
dynamical complexity is often dubbed as chaos, the onset of chaos typically
occurs at the parameters values for which the stable and unstable manifolds
of a saddle point come into contact tangentially.
Basins and attractors In this section we give a sketch on bifurcations which give rise to fractalization of attractor and its basin boundary. The main purpose of this section is to give some results on basin structure of invertible maps and their bifurcations. Especially, we explain basin bifurcations. These basic bifurcations result from the contact of a basin boundary with a chaotic attractor, such a bifurcation leads either to the chaotic area destruction, or a sudden and important modification of this area [GM, M5]. These bifurcations are called contact bifurcations. Different types of fractalization of basin boundary occur, a part of them resulting from a phenomenon of islands aggregation for nonconnected basins [M1]. It is worth noting that the results presented in this section were essentially obtained via a numerical way and using the bifurcation theory tool and the terminology of [M1]. Unfortunately taking into account the complexity of the matter and its nature, it seems difficult to carry out the study with success from another process. The following figures show the corresponding basin structure.
For fixed parameter values, it is possible to define in the phase plane
the basin of an attractor, that means the set of initial conditions giving
to iterated sequences converging towards the considered attractor. Figures
2. (a(1,2), b(1,2), c(1,2), d(1,2)) represent the existing attractors (order
k
cycles, invariant curves or chaotic attractors) and their basins.
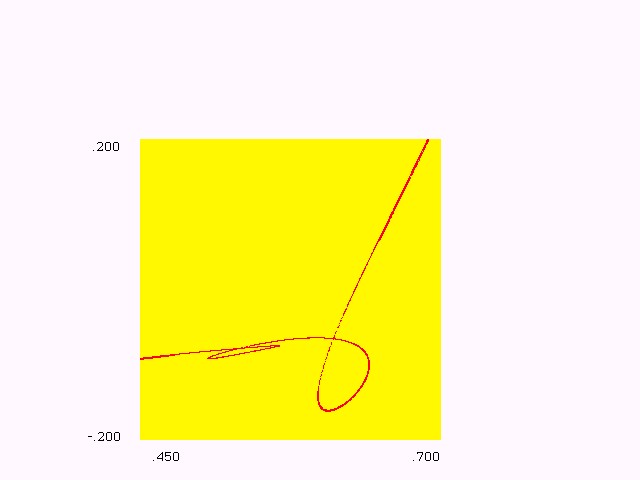
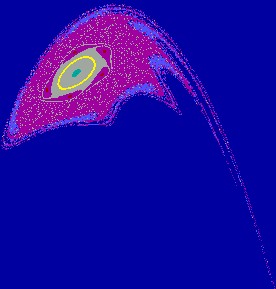
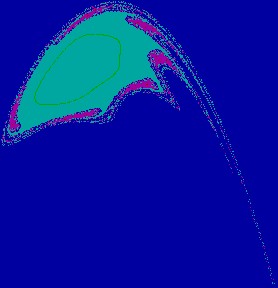
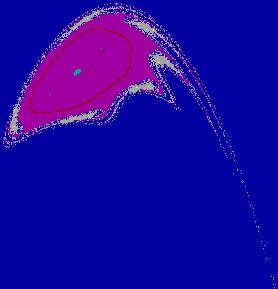
Figure 2(a.1): A closed curve
and its basin e=0.15, m= -1.70, h=0.30.
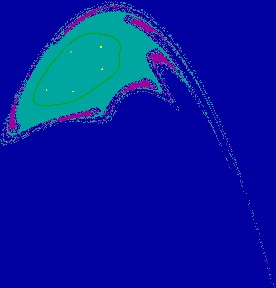
Figure 2(a.2): Enlargement of a part of Fig. 2(a.1).
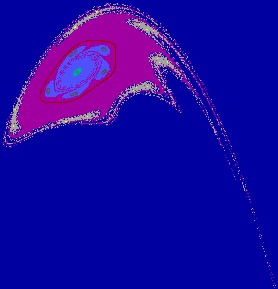
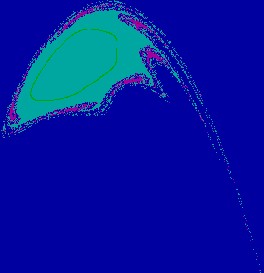
Figure 2(b.1): Chaotic attractor,
tongues appear on
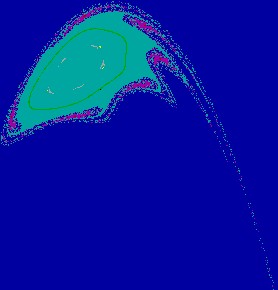
Figure 2(b.2): Enlargement
of a part of Fig. 2(b.1).
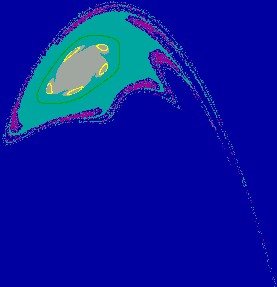
Figure 2(c.1): Contact bifurcation
of the chaotic
Figure 2(c.2): Enlargement of a part of Fig. 2(c.1).
Figure 2(d.1): More and more
loops are created on the boundary
Figure 2(d.2): Situation
just after the disappearance of the
The evolution of attractors and their basins is given
directly in figures, the parameters (e,m)
have been chosen constant and h varies. There exist several ways
in which a dynamical system can become chaotic, of which the period-doubling
route to chaos is the best known. Another scenario leading to chaos is
the destruction of a closed invariant curve, identified here in this model,
the closed curve can lose its smoothness and turn into an irregular invariant
set near a homoclinic structure formed by the intersection of the stable
and unstable manifolds of the saddle point. When h decreases, a
process gives rise to new appearance of tongues on basin boundary, and
there is appearance of oscillations of the closed invariant curve and then
we see a cyclic chaotic behavior. We can see also that the bifurcation
which is put in evidence, corresponds to a limit contact between the basin
boundary ¶D and the chaotic attractor.
A further decrease of the parameter h causes a contact between these
two boundaries which marks the destruction of the basin of attraction.
As argued in Ref [GM], we can see the ghost of this area
destroyed at the contact.
Multistability and Hopf bifurcation This diffeomorphism can be considered as a model giving
rise to a complete and interesting set of bifurcations with birth of cyclic
invariant curves (impossible to obtain with Hénon map) in relation
with quasi periodic solutions, or more complex solutions occuring in the
nonautonomous differential equation . Invariant closed curves are issued
from Hopf bifurcations (see Fig.3 (a, b, c, d, e, f, g, h, i, j, k, l)),
these complicated attracting sets exist for very small parameter ranges.
Arrowsmith & al. [A1] have explained the relationship
between the tongues in Hamiltonian structure and the invariant closed curves
(circles) and clarified various points. Eventual destruction of the Hopf
circles occurs as they grow outwards and their basin boundaries jump inwards
in a series of steps, accumulating on the stable manifolds of subharmonic
saddles.
Figure 3: A sequence of phase
portraits, we can see the basin of period 5,
Properties of Ws(S) and Wu(S) This section is devoted to the study of evolution of attractors when parameters vary. This evolution can involve relations with the attractor basin or homoclinic and heteroclinic bifurcations. In the case of a diffeomorphism, the stable invariant
manifold Ws(S) of
a saddle point S constitutes in general the frontier of the basin
of attraction of an associated attractor A. When Ws(S)
becomes nonconnected each of its connected components approaches again
itself to constitute the frontier of an island. It transforms the connected
attraction basin in nonconnected basin. Holes appear inside the basin,
which becomes multiply connected. All these phenomena generate a very big
sensitivity to initial conditions, due principally to multistability, interconnection
between basins and fractalization of basins.
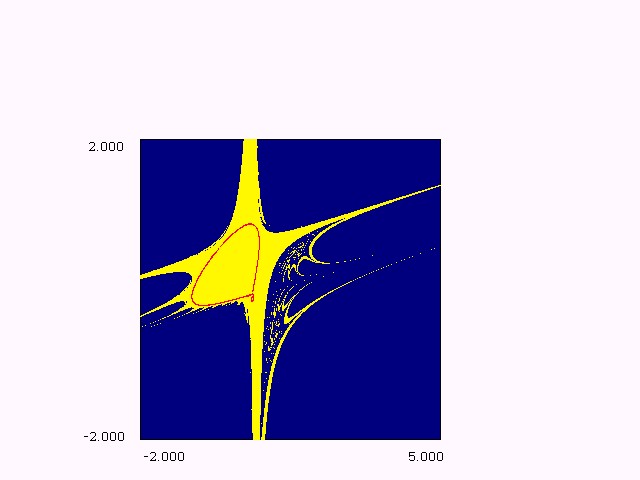
Some properties of invariant curves For fixed parameter values, we plot the attraction basin of an attractor. When there exist several attracting sets, it is possible to define a global basin, that means the set of initial conditions giving rise to bounded iterated sequences, independently of the fact that they converge to one attractor or another. We shall see that particular homoclinic bifurcations which occur are related with the structure of the foliation of the invertible map. Another phenomena can also occur and generate sensitivity to initial conditions. This is the case where there exists two or more different attractors and where their own basins are considered. in this case, one basin constitute holes in the other. This situation is shown in Fig.5, where three different cycles coexist, two basins give rise to holes inside the third one. Proposition 4.1:Consider the invertible map T depending on a parameter l. If the number of connected components of D changes when l crosses through a bifurcation value l*, then the basin D may undergo a qualitative change of one of the following types: (a) simply connected basin « multiply connected basin (when the number of connected components of D changes). (b) modification of the number of holes (lakes) in D, or new arborescent sequence of holes. The numeric studies give to the following results, for
values: e = 0.0, m
= -0.10, h = 1.44.
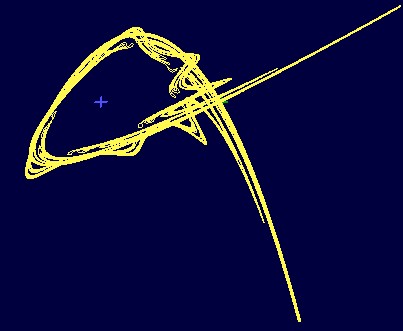
Figure 4: Plot of invariant manifolds of the saddle point (1,0).
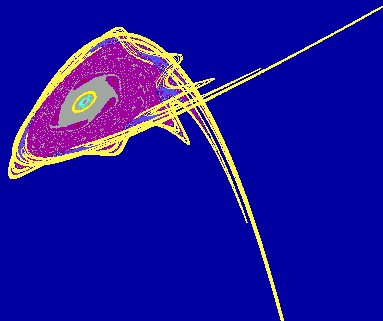
Numerical plot of stable and unstable manifolds of the saddle point at (1,0) shows that the orbit sweeps around (0,0) twice, we can see homoclinic tangle. One has four attractors, the first is stable focus f (0,0) of which the basin of attraction has for external boundary the stable invariant manifold of the saddle point S (1,0). The second is the stable focus cycle of order 5 (represented in five small pink domains in the Figure 5).
Figure 5: f
coexists with an attractive focus of order
5,
These attractors coexist with a cycle of order 6 represented
by grey domains in the Figure 5, and an invariant stable invariant circle
(in yellow color).
Conclusion In this paper, specific bifurcations arising in invertible
maps of quadratic type have been studied. These bifurcations concern the
evolution of chaotic attractors, which appear or disappear by contact bifurcations,
with their own basin boundary. In such maps, chaotic attractors can be
issued of Hopf bifurcation giving rise to invariant closed curves which
evolve into chaotic attractor or of a succession of period-doubling bifurcations
[F1, B2, B3]. As
usually in many nonlinear systems, important changes can occur with small
changes of parameter values.
Acknowledgment This work was supported by grants from ANDRU under N°:
CU39904.
References [A1] D.K. Arrowsmith, The Bogdanov Map: Bifurcation, Mode Locking, and Chaos in Dissipative System, Int. J. Bifurcation and Chaos, 3, 803-842 [1993]. [A2] D.K Arrowsmith & C.M. Place, An Introduction to dynamical systems, Cambridge University Press [1990]. [A3] V.I. Arnold, Lecture on bifurcations and versal systems, Russ Maths. Surveys 27, 54 [1972]. [B1] R.I. Bogdanov, Bifurcation of the limit cycle of a family of plane vector fields, Trudy Sem. Petrovsk. 2, 23. In Russian: the english translation is Sel. Math.Sov. 1(4), 373-88 [1981]. [B2] H. Broer, C. Simo & J.C. Tatjer, Towards global models near homoclinic tangencies of dissipative diffeomorphisms, Nonlinearity, 11, 667-770 [1998]. [B3] M. Bosch, J.C., Tatjer, On the codimension-two bifurcation in families of one and two-dimensional maps, ECIT Batschuns (Australia) [1989]. [F1] D. Fournier, H. Kawakami & C. Mira, Feuilletage du plan des bifurcations d'un difféomorphisme bidimensionnel. Doublement de l'ordre des zones sources et des zones échangeurs. C.R. Acad. Sc. Paris, sér 1, 301(5), 223-320 [1986]. [F2] D. Fournier, Contribution à l'étude de structures de bifurcations rencontrées en dynamique chaotique, Thèse de doctorat d'état (Toulouse) [1987]. [H1] M. Hénon, A two-dimensional mapping with a strange attractor, Commun. Math. Phys. 50, 69-78 [1976]. [H2] P. Holmes & D. Whitley, Bifurcation of one and two dimensional maps, Phil. Trans. R. Lond. A311, 43-102 [1984]. [M1] C. Mira, Chaotic dynamics, World Scientific Publishing. Co. Pte. Ltd [1987]. [M2] C. Mira & C. Rauzy, Fractal Aggregation of Bassin Island in Two-Dimensional Quadratic Non-Inversible Maps, Int. J. Bifurcation and Chaos, Vol. 5, No. 4 [1995] 991-1019. [M3] C. Mira, Accumulations de bifurcations et structures boites-emboitées dans les récurrences et transformations ponctuelles, Proceeding of the VIIe International Conference on Non Linear Oscillations, Band I 2, 81-93 [1975]. [M4] C. Mira, D. Fournier, L. Gardini, H. Kawakami & J.C. Cathala, Bassin bifurcations of two-dimensional non-invertible maps Fractalization of basins, Int. J. Bifurcation and Chaos, vol. 4, no. 2, pp. 343-382 [1994]. [M5] G. Millérioux, Modèles par Transformations Non Inversibles et Application à la Sécurité des Communications Synchronisation du Chaos, Thèse de Doctorat de L'INSA ( Toulouse) [1997]. [GM] I. Gumowski & C. Mira, Bifurcations déstabilisant une solution chaotique d'un endomorphisme du 2 ndordre, Comptes Rendus Acad.SC; Paris A286, 427-431(1978). [T] J.C. Tatjer, Invariant manifolds
and bifurcations for one-dimensional and two dimensional dissipative maps,
PHD. Thesis University of Barcelona [1990].
|