Some Monohedral Tilings Derived From
Regular Polygons
Paul Gailiunas
25 Hedley Terrace, Gosforth
Newcastle, NE3 1DP, England
email: Paul
Gailiunas
Abstract
Some tiles derived from regular
polygons can produce spiral tilings of the plane [1]. This paper considers some
more general classes of tilings with tiles derived from regular polygons, some
have central symmetry, many have periodic symmetry, some have both, and a few
have no symmetry at all. Any of these tiling patterns could be the basis for
some interesting mathematical art, for example by colouring or decorating the
tiles.
Using Regular Polygons to Make Tiles
Overlapping
copies of a regular polygon around a common vertex produces a pattern of rhombi.
A tile can be chosen bounded by sections of the perimeters of three of the polygons
(figure 1). A section of the perimeter of a polygon will be termed a polygonal
arc.
If
the polygon is a regular n-gon then the angles of the rhombi are 1/n,
2/n, 3/n ... (measured as fractions of a full rotation; multiply
by 360 for degrees, or by 2π for radians). If the arcs
are measured in units equal to a side of a polygon then by inspection: t = r + s, Ð R = r/n, Ð S = (t - 1)/n, Ð T = 1/2 - s/n
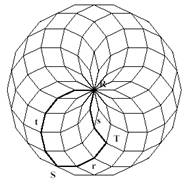
Figure 1. The construction of a tile.
Copies of any tile with r = 2 (or 1) will tile the plane. There are five types of isohedral tiling (every tile can be transformed into any other by a symmetry of the tiling, so all tiles are the same).
Adjacent rows can be oriented:

identically

reflected

rotated by180°

reflected and rotated by180°
or the tiles are

not lying in visually obvious rows
The tiles meet at two types of vertex, where the angle sum = 1, for any value of n.
Figure
2. The tiling has only two types of vertex.
1/2 - 1/n + (t - 1)/n + 1/2 - s/n = 1 + (t - s - 2)/n = 1 + (r - 2)/n = 1
2 (1/2 - 1/n) + r/n = 1 - 2/n + r/n = 1
In general it will not be possible to tile the plane with tiles made
like this because every convex section must be matched by a concave section,
which can never occur. There are two special cases: if r = 1 then the arc is
neither concave nor convex; if r = 2 then in all cases the tiles will
fit as illustrated.
If ÐS is an exact fraction of a full rotation then a
centrally symmetric tiling is possible.

The tiling consists of V-shaped sections with ÐS at the apex. Each section is in two parts. The tiles in one part are mirror images of the tiles in the other part. This is the underlying structure of all centrally-symmetric tilings with tiles derived from overlapping polygons.
There are some special tiles with unique properties. One, found by
Robert Reid, has n = 12 and s = 2, so t = 4, since r
must be 2. It forms a standard centrally symmetric tiling,

and another

that is arranged around a dodecagon consisting of three tiles. Another has n = 10 and s = 3,
so t = 5 and Ð S = 2/5, the interior angle of a 10-gon, so the arcs
r and t form a single arc of 7 sides. This tile has been investigated by Haresh
Lalvani [2], and it will appear again as a special case of another type of
tile. It allows spiral tilings of the plane [3].
Biconcave Tiles
In figure 1, if the
arc, r, is reflected in the line ST a new tile is produced. This is equivalent
to removing a section from the tile that is bounded by two polygonal arcs that
has apical angles of (r - 1)/n. The new tile has angles:
Ð R = r/n
Ð S = (t - 1)/n - (r - 1)/n
= (t - r)/n = s/n
Ð T = 1/2 - s/n - (r - 1)/n
= 1/2 - (r + s - 1) n = 1/2 - (t - 1)/n
This time the length
of the convex arc is equal to the combined length of the concave arcs, and all
such tiles will tile the plane. Figure 3 shows how three isohedral tilings are
possible.
We can see that any of these tiles will work because for any tile the angle sum at each vertex of the tiling is always 1. The tile can be seen as a modified parallelogram.
Ð R + Ð S + Ð T + 1/2 - 1/n = r/n + s/n + 1/2 - (t - 1)/n + 1/2 - 1/n = 1 + (r + s - t)/n = 1
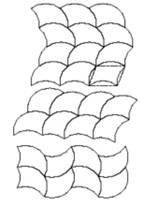
Figure 3. All biconcave tiles will tile the
plane.
When s = 2 there are two further possibilities because the tiles can fit together in a staggered fashion, related by either a rotation of 180°

or a glide reflection.

Robert Reid has discovered another possibility. If tiles can be arranged
so that they meet at edges on convex polygonal arcs in principle tilings are
possible with t = r + s + 2 (as in figure 2), but it works
only if t = n/2 + 1. Again three isohedral tilings are possible:
with only
translational symmetry;

with glide reflection;

with glide reflection in another direction.

Lalvani’s tile with n = 10, r = 2, s = 3, t = 5 can
also be seen as an example of this type with n = 10, r = 1, s =
3, t = 6, since a polygonal arc of length 1 can be considered as either
convex or concave.
If Ð R is an exact fraction of a full rotation it is possible to produce a
centrally symmetric tiling that consists of two-part V-shaped sections in a
similar way to the example in figure 3. When both r and s divide n
two centrally symmetric tilings are possible, for example a tile with n
= 18, r = 2, s = 3 will allow a tiling with rotational symmetry
of order
6
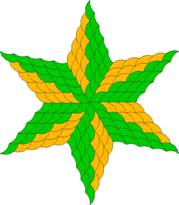
and another of order 9.

Similarly the previous example of one of Reid’s tiles with n = 12,
r = 3, s = 4 will allow a tiling with rotational symmetry of order
3
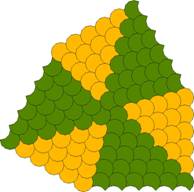
and another of order 4.

The value of t is determined by r and s, and four
tiles will always fit around a vertex if angles of each type are present (as in
figure 3), so all such tilings with the same values of r/n and s/n
have identical structures. In the limit the tiles will have sides that are
circular arcs (provided that they have the same radius, and the arc lengths
satisfy t = r + s). Provided that it does not depend on
some specific number (such as the tilings like figure 2, when r must be
2) any tiling has an infinite series of equivalent tilings, including the
limiting one with circular arcs. The general case of spiral tilings described
in [1] is of this type, although the special cases (most of the examples) are
not, since they depend on particular number properties.
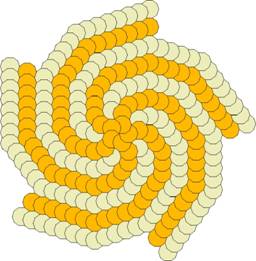
An interesting example is provided by the three-armed spiral using a
tile from a hexagon (figure 13 in [1]). Doubling the values of n, r and s
gives a tile with n = 12, r = 2, s = 4, t = 6 with
the special property that it can be dissected into two tiles with n =
12, r = 1, s = 4, t = 5. Two three-armed spirals that use
this tile were described in [1], this is a third (figure 4). Figure 5 shows the
limiting case of this tiling, when the edges of the tiles are circular arcs.
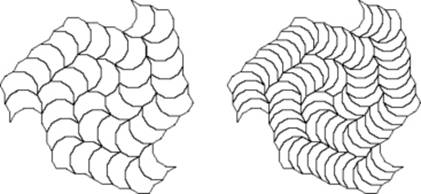
Figure 4. A three-armed spiral tiling dissected.
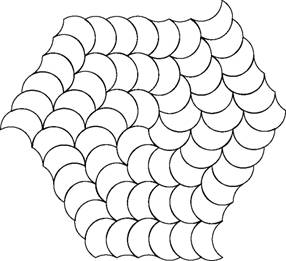
Figure 5. A three-armed spiral tiling with circular arcs.
Special Cases
Figure 6 shows an additional way that some tiles can fit together.
Usually there are no further tilings, apart from the cases when s = 1
and s = 2.
There are two types of vertex, both valency = 3. The same condition is satisfied by both types
Ð R + Ð S = 1/2 - 1/n
r/n + s/n = t/n = 1/2 - 1/n
t = n/2 – 1
Ð T = 2/n
1/2 - (t - 1)/n = 2/n
t = n/2 – 1

Figure
6. An additional type of tiling.
If s = 2 the tiles can also fit in a staggered
way that is analogous to the tiling in figure 2. The tile with n = 8, r
= 1, s = 2 (so that t = 3 = n/2 ‑ 1) is special
in several ways, and allows eleven different isohedral tilings, five as
described in the first section since the side of l can be considered to be
convex (Grünbaum and Shephard types 41,

47,

43,

42,

44),

two of the staggered type since s = 2 (types 2,

4),

one of the special type since t = n/2 – 1 (type 6),

one that is peculiar to tiles with r = 1 (type
53),

and two that are possible because the tile with n =
8, r = 2, s = 2 can be dissected into two copies of it (types
43,

51).

It is quite easy to produce a tile that will allow
any number of different isohedral tilings [4]. This tile allows ten different
types of isohedral tiling, which is probably the greatest number of any tile.
The tile with n = 10, r = 2, s = 2 (so that t
= 4 = n/2 ‑ 1) is even more remarkable. It has mirror symmetry, so
there are fewer different isohedral tilings, but it is possible to form
boundaries in quite flexible ways between areas of isohedral tiling

that are oriented in different directions. Since s = 2 the tiles
can also fit in a staggered way, allowing boundaries to meet, either symmetrically

or asymmetrically.
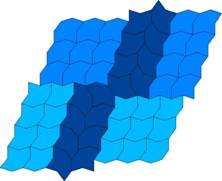
A centrally symmetric tiling

can be constructed using this feature. A particularly
unusual tiling has an additional row
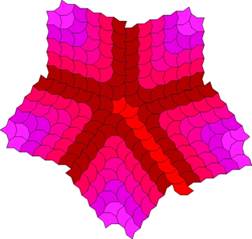
inserted, breaking the symmetry.
Another centrally symmetric tiling can be seen as a spiral of either sense.

Periodic Tilings
There are two cases when central regions of centrally-symmetric tilings
will themselves tile the plane periodically: when they are hexagonal or square,
possibly modified. Figure 7 illustrates how the tile with n = 6, r
= 1, s = 2, t = 3 can form hexagons of various sizes, but there
are equivalent tilings with these values multiplied by any integer. As we have
already seen (figure 4) the special case when they are doubled produces a tile
that can be dissected into two smaller congruent tiles (n = 12, r
= 1, s = 4, t = 5). The resulting tilings, based on either basic
hexagons

or the enlarged version can be quite attractive.

The process of enlargement can continued indefinitely.
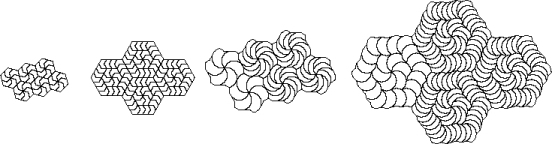
Figure 7. Periodic tilings based on hexagons.
The square is the basis for the other type of periodic tiling (n =
4, r = 1, s = 1, t = 2), and again the case when these values
are doubled is special because it produces a tile that can be dissected into
two smaller congruent tiles (as in isohedral tilings type 43

and 51

above), but in two different ways, since it has mirror symmetry (figure
8). This allows many variations of the basic tiling.

Again enlargement is possible,

with different dissections,

and the enlargement can be continued.


Figure 8. Basic variations on the periodic tiling based on squares.
Further Possibilities
Although a few tilings with tiles having r = 1 have been
considered there are probably many more to be found, since the constraint
imposed by matching concave and convex arcs is relaxed. There has been no consideration of tilings
derived from polygons having an odd number of sides, which seem to be more
limited, but they are known to allow at least one type of spiral tiling [5],
and many tilings using the reflex equilateral pentagon are known [6]. Versatiles [7] appear in a range of spiral
tilings, but only the pentagonal versatile [8] seems to allow a particularly
wide range of tilings, nevertheless there are probably more to be discovered.
Another possibility yet to be explored in any detail is the use tiles with
boundaries consisting of more than three polygonal arcs.
Many of these tilings are aesthetically pleasing as they are, and they
can be coloured in many different ways. The resulting patterns could have
applications in architectural details (literally tilings), or in textile
design, or simply as works of mathematical art in their own right.
References
[1] Gailiunas P.,
"Spiral Tilings" Bridges 2000, pp.133-140. Copied at http://www.mi.sanu.ac.yu/vismath/gal/index.html
[2] US Patent
4,620,998, 1986, cited in Lalvani H.,
Meta Archtecture, in Architecture and Science (ed. Di Cristina G.),
Wiley Academy, 2001.
[3] Stock D.L. and
Wichmann B.A., "Odd Spiral Tilings", Mathematics Magazine vol.73,
no.5, Dec 2000, pp.339-347.
[4]
Grünbaum B. and Shephard G.C., Tilings
and Patterns, Freeman,
1987, p.50.
[5] Hatch G.
"Tessellations with Equilateral Reflex Polygons", Mathematics
Teaching, no.84, Sept.1978, p.32.
[6] Simonds D.R.,
"Central Tessellations with an Equilateral Pentagon", Mathematics
Teaching, no.81, Dec. 1977, p.36.
[7] Grünbaum B. and
Shephard G.C., "Spiral Tilings and Versatiles", Mathematics
Teaching, no.88, Sept. 1979, pp.50‑1.
[8] Rice M. and
Schattschneider D., "The Incredible Pentagonal Versatile", Mathematics
Teaching, no.93, Dec. 1980, pp.52‑3.