Form and Symmetry: Art and Science
Buenos Aires Congress, 2007
HIDDEN SYMMETRIES AMONG PRIMES
Gustavo Funes, Damian Gulich, Leopoldo Garavaglia and Mario Garavaglia
Name:
Gustavo FunesAddress: Departamento de Fisica, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, y Laboratorio de Procesamiento Láser, Centro de investigaciones Ópticas, La Plata, Argentina.
Email: gfunes@ciop.unlp.edu.ar
Name: Damián Gulich
Address: Departamento de Fisica, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, y Laboratorio de Procesamiento Láser, Centro de investigaciones Ópticas, La Plata, Argentina.
Email: dgulich@ciop.unlp.edu.ar
Name: Leopoldo Garavaglia
Address: Calle del General Pingarrón Nº 3
Portal 10, 3º C
Getafe, Comunidad de Madrid, España.
Email: garavaglia_leo@hotmail.com
Name: Mario Garavaglia
Address: Departamento de Fisica, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, y Laboratorio de Procesamiento Láser, Centro de investigaciones Ópticas, La Plata, Argentina.
Email: garavagliam@ciop.unlp.edu.ar
Abstract: We have established a new way of studying simple mathematical problems in a graphical way. Copying Eratosthenes we introduce a sieve in the form of layers of prime multiples represented as binary bands. Those layers have a totally determined frequency and they are fully symmetric. By means of this method we will see that the position of prime numbers is far away from being random, on the contrary, it has a totally determined structure, at least not directly. Finally we will see that some unsolved problems like Goldbach conjecture and related ones, are based in hidden symmetries to be proved.
1 INTRODUCTION
For centuries many mathematicians, scientists and erudits studied the problem of the location of prime numbers. Some of them found formulas that based on natural numbers will give possible primes, like Fermat and Merssene. Nevertheless, no one has found a single formula that gives all prime numbers as a result. Nowadays, prime search algorithms are based on probabilistic mathematic structures, although some mathematicians think that prime structure is totally determined by certain rules.
The location of prime numbers does not follow a defined pattern, and it has an evident lack of symmetry. For that reason it is remarkable the existence of twin primes, (prime numbers separated by 2), Cousin primes (primes separated by 4), sexy primes (primes separated by 6), and even triplets and cuadruplets of primes. Recently, it has been demonstrated that there exist arbitrary large arithmetic progressions of primes (Terence Tao). It is evident that these groups of primes, or constellations, are amazing because the whole prime structure has no evidence of certain order, it has no series expansion, and has no symmetry.
2 ABOUT PRIME LOCATIONS AND THE USE OF DIGITAL ROOT
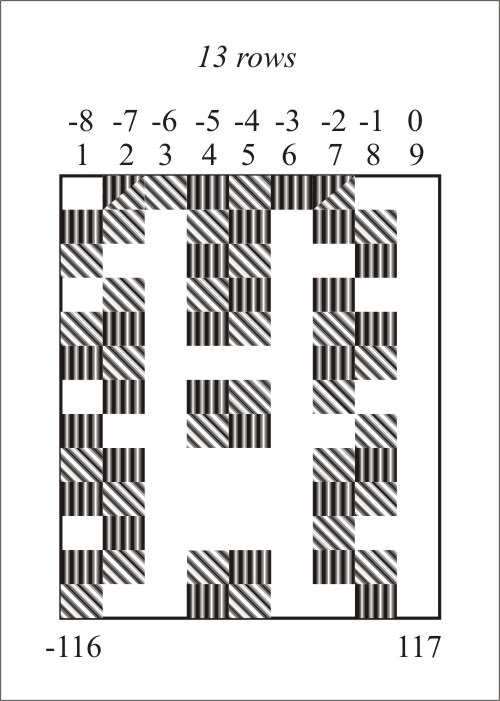
Based on a previous work we will use the digital root in order to establish a matrix representation of numbers in nine columns, each of them corresponding to a determined digital root. By doing this we can see that prime numbers are located in certain columns. In order to follow the location of primes we painted the boxes which contain prime numbers. As expected we find patterns of primes, but the most remarkable thing is that these patterns are reflected vertically and mirrored horizontally when we use negative primes. These patterns can be observed in the following pictures at Figures 1 and 2.

Figure 1: First prime patterns obtained by the use of digital root
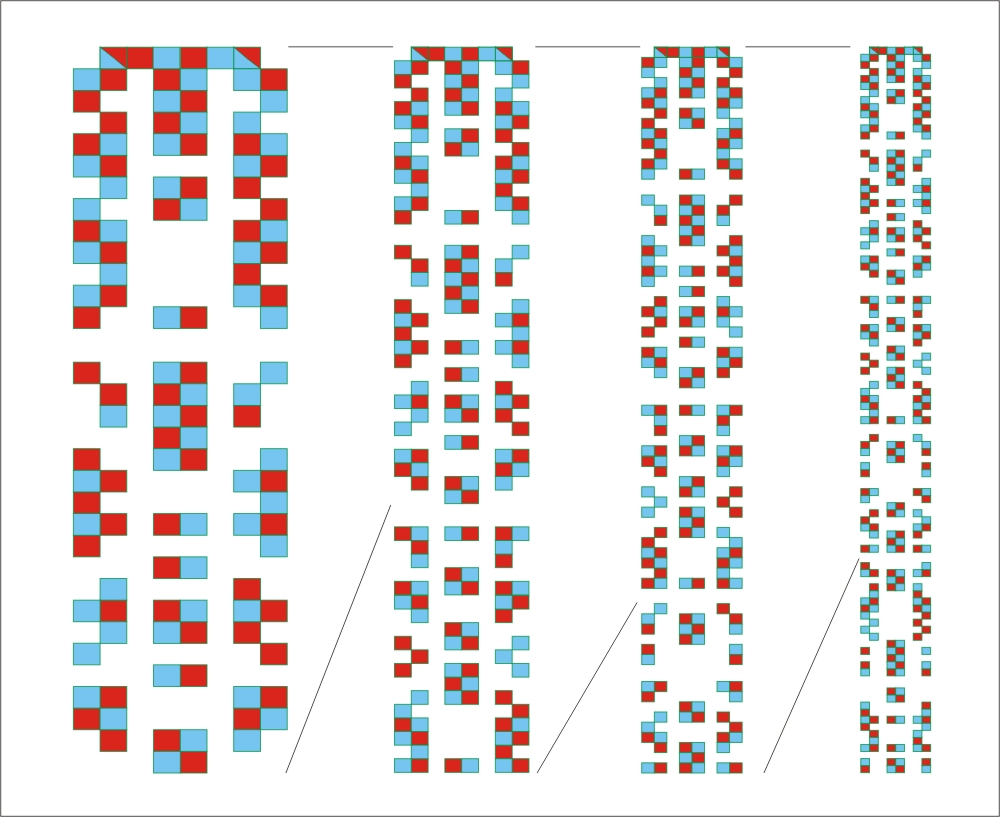
Figure 2: Sequential zoom of the pattern and the hole figure up to 1000
According to this scheme we can classify all numbers in nine families one for each column and even in only six families. The classification in six families is the lowest possible and determines that all primes greater than 3 belong to two different families. Here we present this classification and their corresponding formulas:
where n = 0, ± 1, ± 2, ± 3, ...
Except 2 and 3, all the others prime numbers are of the form as 1+6.n and 5+6.n.
In order to visualize these classifications we use the binary bands. These bands are a series of boxes painted in different colors, where each color represents any specific property of the number. In our case we use the binary band to differentiate primes from non primes. In the following example (See Figure 3) we show families 1+6.n, 3+6.n, 5+6.n, and the procedure to build up the corresponding Odd binary band.
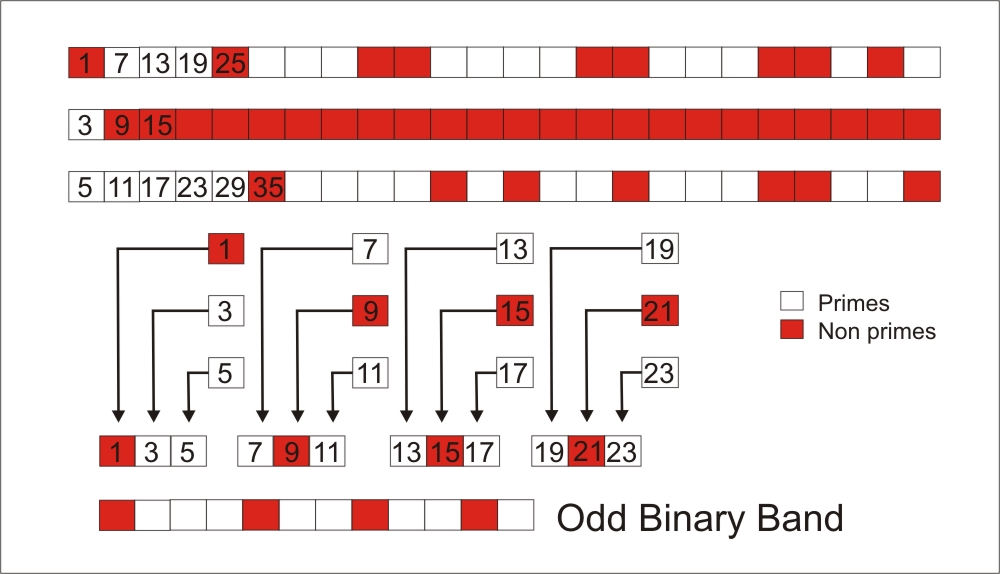
Figure 3: Odd families and the odd binary band.
3 ABOUT LAYERS OF COMPOSITE NUMBERS
We will see a series of odd numbers represented as a binary band. In Figure 4 we see how we build up each of them. In this particular case, black boxes will represent multiples of primes, and whites will represent nothing yet. The first layer corresponds to multiples of 3; the second corresponds to multiples of 5, and so on.

Figure 4: Odd binary band and its decomposition in layers
After the inspection of Figure (4) we may identify some layer properties:
* Each layer begins in a multiple of 3.
* In the first layer the period is 2 times 3, where 3 is the characteristic prime.
* In general, for a given prime P the period of its layer is 2P
* Then, copying Eratosthenes, white boxes that remain after overlapping all the layers correspond to prime numbers.
Considering each multiple as root we can imagine a sinusoidal wave whose period in boxes is 2xP where P is the characteristic prime of the layer, as in Figure 5.
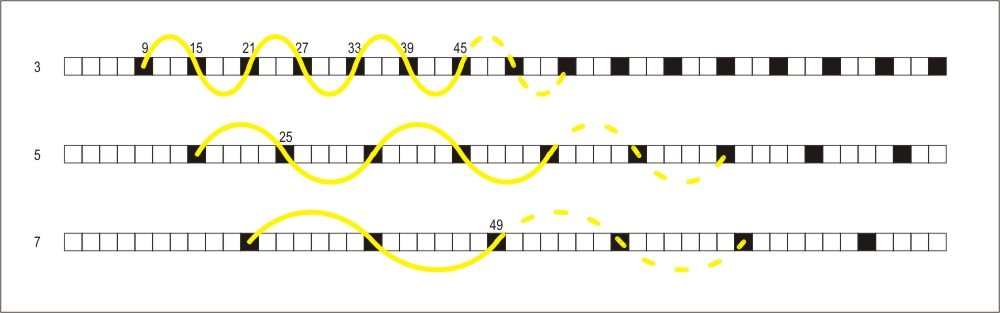
Figure 5: Visualization of the periods of layers.
Taking this fact into account we can postulate the following properties related to the periods:
When going far from the origin we will have to add more layers to have a complete set of prime numbers. It means that if there is a missing layer there will be several numbers labeled incorrectly as primes.
Given an odd number N, the amount of layers that are needed up to that number is less than the amount of primes before N, and there exist a prime number P so that:
3P≤N
The amount of layers needed to sieve all primes up to N is equal to the amount of primes up to N/3. Nevertheless, if we observe in detail Figure 4; we see that when adding a new layer the first elements of it are in coincidence with elements of other previous layers. That is because the composite number –all of which are odd numbers– represented as black boxes are 3x3, 3x5, 3x7,..., that is 3 times all primes for the first layer; 5x3, 5x5, 5x7,..., that is 5 times all primes for the second, and so on. Then, by using this way we are repeating many composite numbers, as 3x5 and 5x3, for instance. Therefore, each layer will begin to sieve in the number which is the square of the characteristic prime that identifies each layer, i.e., 5, 7, 11, 13, and so on.
We see that in each layer odd numbers represented by black boxes are regularly spaced, then each layer is totally symmetric in certain points, although they are glided. These points of symmetry are reflected in the final result, which is the binary odd band with primes as white and composites as black boxes, resulting from the sieve effect produced by overlapping all the layers. The fact that the whole odd band has neither symmetry nor order is based on the glides of the layers, and that they all have a different prime frequency. Therefore, as each layer is symmetric, there exist hidden symmetries of composite numbers among primes. Those symmetries are seen indirectly on primes through the existence of twins, cousins and other constellations. When we have a constellation of three primes separated by 4, for example, the prime on the middle represents symmetry, at least along 12 numbers. This symmetry is semi-symmetry because it represents only a part of the odd band.
4 ON SEARCH FOR LOST SYMMETRY
We will start by introducing some unsolved problems and find out why symmetry is so important for them. First, we have Goldbach´s Conjecture, which is intimately related with Polignac´s conjecture, and a particular case of the last one is the twin prime conjecture. We will enunciate rapidly these three:
* Goldbach (strong): All even number greater than 2 is represented by the sum of two primes.
* Polignac (weak): All even numbers can be represented as the difference of two primes.
* Twin Prime: There exist infinitely many twin primes, it means, pairs of primes whose difference is 2.
We will analyze those problems by introducing the graphical mode of binary bands. Goldbach’s Conjecture is based in sums of primes. We will take a binary band and we will compare it with itself, if we make the addition of all numbers with each other we will obtain the doubles of all numbers, but when inverting or reflecting one of the bands, we will obtain a constant sum. While gliding the bands we find different even numbers obtained by the sum of two odd numbers. All white coincidences represent a sum of prime numbers. This is the equivalence of Goldbach’s conjecture presented in a graphical form, as it appears in Figure 6.

Figure 6: Graphical representation of Goldbach Conjecture.
On the other hand, we have Polignac’s conjecture. This conjecture is based in the difference of odd numbers. In the graphical form we will have an odd band compared with a copy of itself but glided one box. Those numbers are all separated by 2. If we glide again we will have numbers separated by 4, and so on. When white coincidences between the original band and the glided one occur, then we will have prime numbers whose difference is an even number. Another way of observing graphically Polignac’s conjecture in accordance with the graphical representation of Goldbach’s problem is based on the use of negative odd numbers. When using a band of odd numbers –negative included– we compare this infinite band with infinite copies of it but inverted. Those copies are glided so we can cover all even numbers in each glide. In such scheme, we will see Polignac and Goldbach’s regions in a single graphic, as in Figure 7.
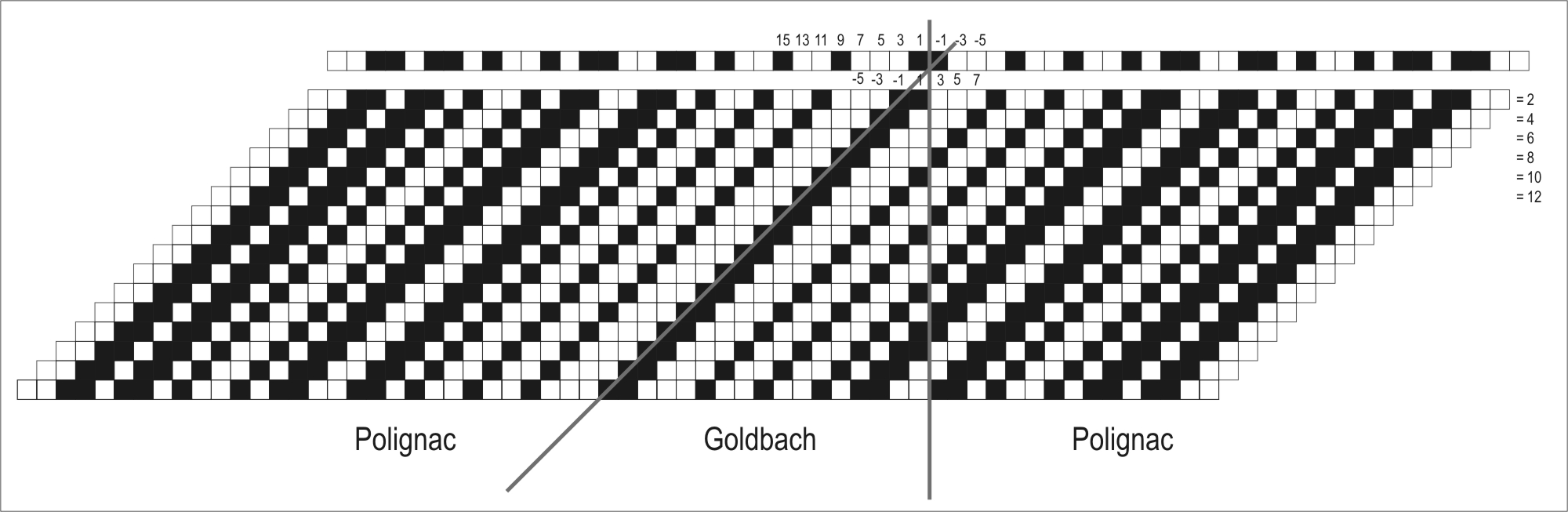
Figure 7: Graphical relation between Goldbach and Polignac conjectures.
Considering the question of symmetry, Goldbach’s conjecture claims white coincidences while comparing a band with its inverted copy. It means that there is a point in the band from where we can see two primes equidistant, one to the right and the other to the left, and its sum represents a given even number. This point, that could be an odd number or an even one, is a point of hidden symmetry. This symmetry can not be seen in the whole picture, and it does not indeed exist, because it is covered by composite numbers of the layers of prime multiples. What we are doing here is comparing the topological structure of a band with an inverted copy of itself, so that the topological structure of the band is also inverted creating a symmetric pattern of white coincidences, as it is shown in Figure 8. On Figure 9 we see how these symmetric patterns are hidden in the odd binary band for some examples.

Figure 8: Hidden symmetries in the Goldbach problem
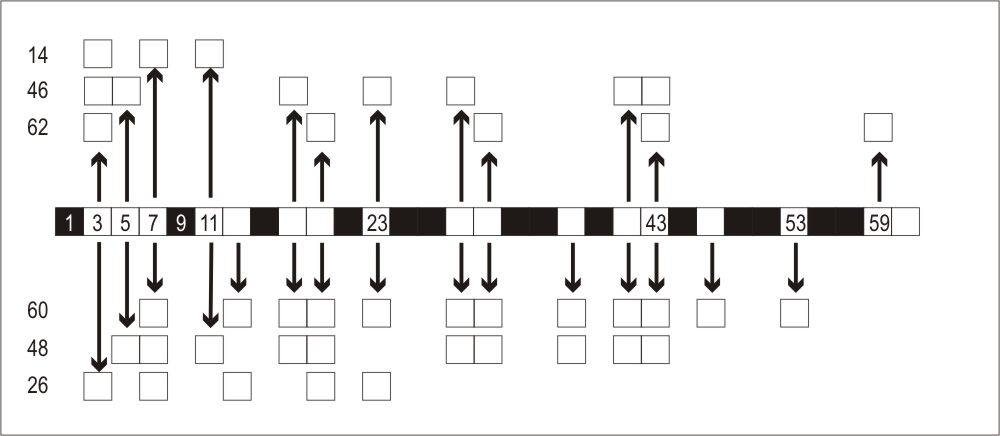
Figure 9: Some examples of hidden symmetries shown on the odd binary band
To have a complete view of these symmetries we will see all the patterns that represent each even number in the following Goldbach triangle:

Figure 10: Goldbach triangle
This Goldbach triangle is obtained as the result of overlapping the odd binary band with itself inverted. But in a close inspection it is the moiré pattern of two odd binary bands as we can see in Figure 11.
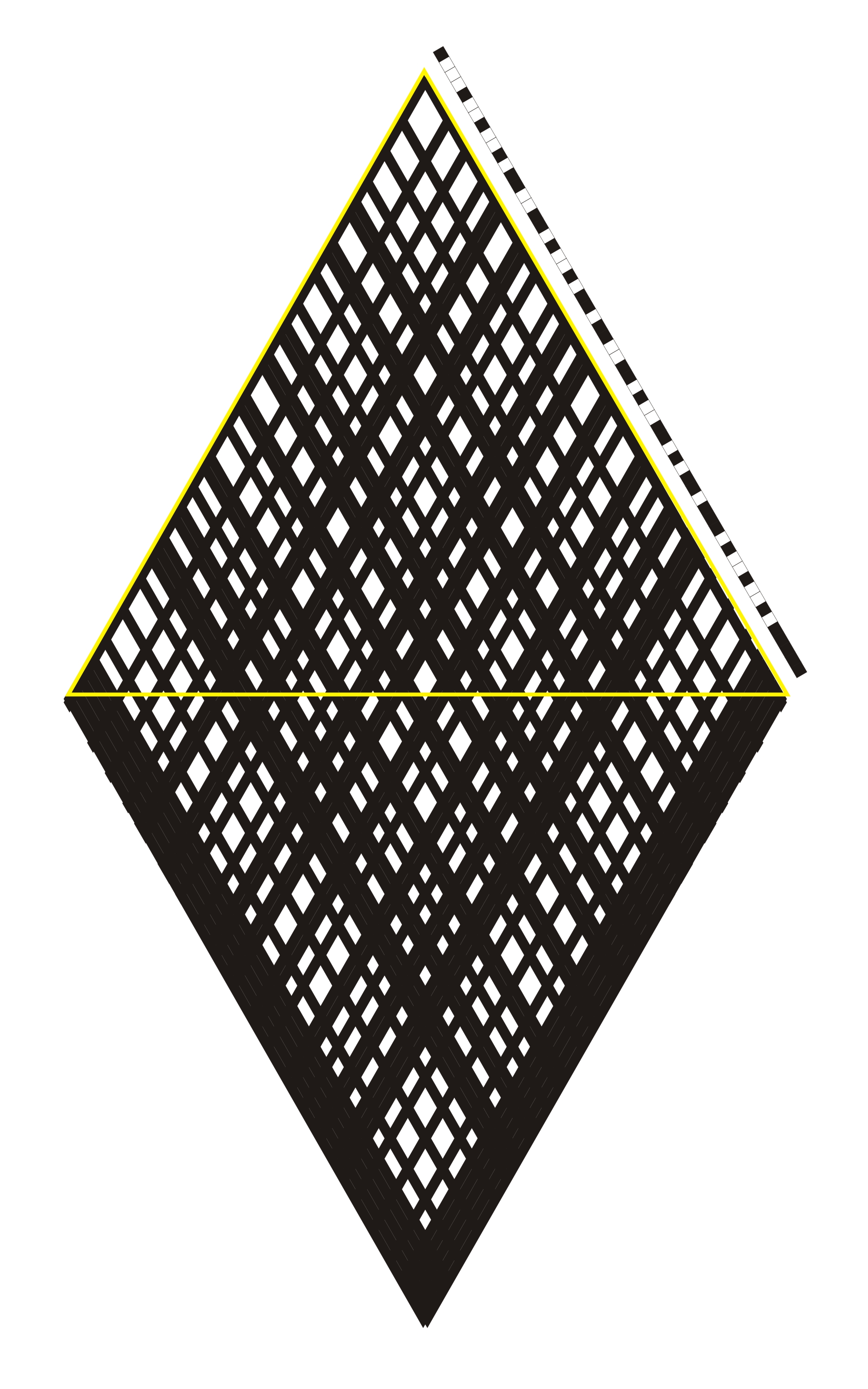
Figure 10: Moiré pattern of odd binary bands.
The fact that Goldbach’s conjecture has been verified up to 1018, signifies that the hidden symmetry really exists up to that point, at least.
5 CONCLUSIONS
We have seen that the structure in which are based all primes is far away from being random. If we speak in a rigorous way, when something is random, there is no memory in the process, it means, two successive numbers have no relation, or one number has no relation with the preceding or the next in the series. However, in the case of a series of odd numbers, where we have allocated the primes and the composites, there is a relation between numbers. This relation is presented here in the form of layers of prime multiples. Copying Eratosthenes´ sieve in a graphical representation we have seen how we pass from completely ordered layers to a completely unpredictable scheme of prime and non-prime numbers. But the question is: Are the prime locations so disordered or random? Certainly, it seems disordered and unpredictable, but there are certain rules that have to be fulfilled. For example, there are no clusters of four consecutive primes. And there are no clusters of three consecutive primes aside from the triplet [3,5,7]. Thiese rules must be applied as a consequence of the "multiples of three". Obviously we know that there exists an infinite amount of clusters of composite numbers whose length varies from 2 to infinite. Finally, we have seen that the graphical form of study of these numerical problems reveal symmetry properties that could not be seen at first sight.
References
Dickson, Leonard Eugene. (1952), "History of the theory of numbers", (Vol. 1), New York, N. Y.: Chelsea Publishing Company.
Funes G., Gulich D., Garavaglia L., and Garavaglia M. (2007), "About Goldbach strong conjecture". arXiv:0708.3704 [math.GM].
http://arxiv.orgGaravaglia, Leopoldo and Garavaglia, Mario. (2007), "On the location and classification of all prime numbers". arXiv:0707.1041v1 [math.GM].
http://arxiv.orgHardy, G. H and Wright, E. M. (1962), "An introduction to the theory of numbers", (4ta ed.), Oxford: Oxford at the Clarendon Press