|
From Liki-designs to cycle matrices: The
discovery of attractive new symmetries
Paulus Gerdes Ethnomathematics
Research Centre,
E-mail: pgerdes@virconn.com
Lunda-designs Liki-designs constitute a particular class of Lunda-designs. In the final part
of Geometry from Africa (1999) I explained how
I discovered Lunda-designs in the context of analysing mathematical aspects
of traditional sona pictograms from Angola and then I presented briefly
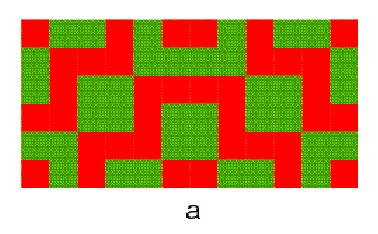
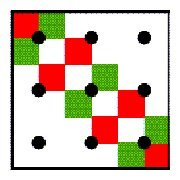
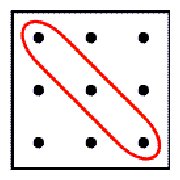
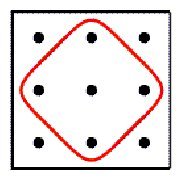
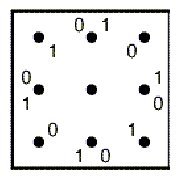
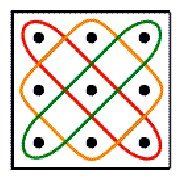
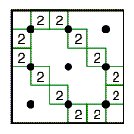
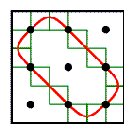
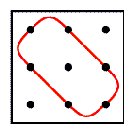
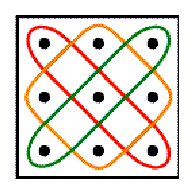
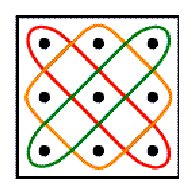
some properties and generalisations of Lunda-designs. Figure
1 presents some examples of Lunda-designs. In several earlier papers
(1990,
1997a, 1999b:
http://members.tripod.com/vismath/paulus/)
and book chapters (1993-4, 1995: 379-428,
1997:
275-300), and in the book
Lunda-Geometry: Designs, Polyominoes, Patterns,
Symmetries (1996) I analysed geometrical properties
of Lunda-designs. As Lunda-designs are often aesthetically attractive,
some papers deal with art and Lunda-designs (2002,
2002a).
Another paper (2000) shows how infinitely many magic
squares may be constructed from Lunda-designs. My contribution to the conference
Symmetry
2000 presents further generalisations of the concept of Lunda-design
(2001). Lunda-designs of Celtic knots are analysed in
(1999a).
Figure 1 In one of the chapters
of my forthcoming book The beautiful geometry and linear algebra of
Lunda-designs (2002b) I explain in detail how experimentation
with Liki-designs, a particular class of Lunda-designs, led me to the discovery
of cycle matrices. The present paper gives an overview.
Liki-designs It was on the eve
of the fourth anniversary of my daughter Likilisa that I started to analyse
a particular class of Lunda-designs. As these designs turned out to have
some interesting properties I gave them the name of Liki-designs.
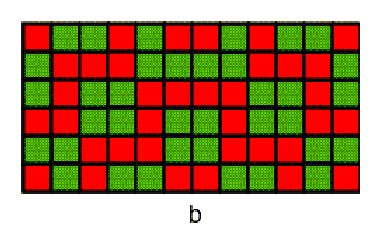
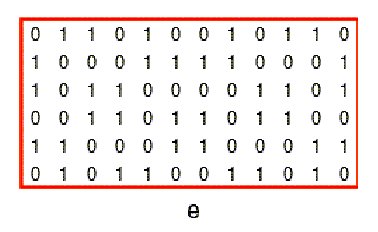
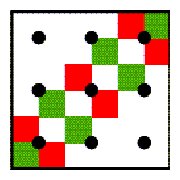
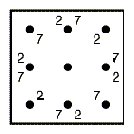
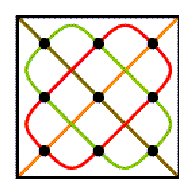
Figure 2 Figure
2 presents an example of a Liki-design with its associated Liki-matrix.
The matrices are obtained by substituting the unit squares of one colour
(in this case red) by 0s and the unit squares of the other colour (green
in this case) by 1s.
Figure 3 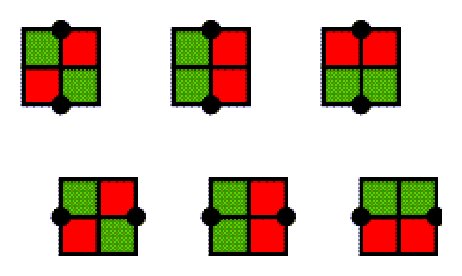
Figure 4 Lunda-designs are characterised by the following two local (two-colour) symmetry properties: 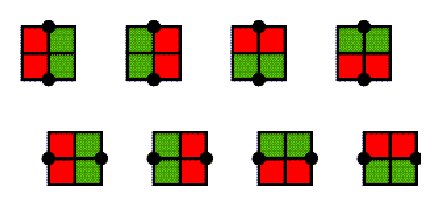
Figure 5 In the case of Liki-designs, the second property is substituted by the following stronger condition: 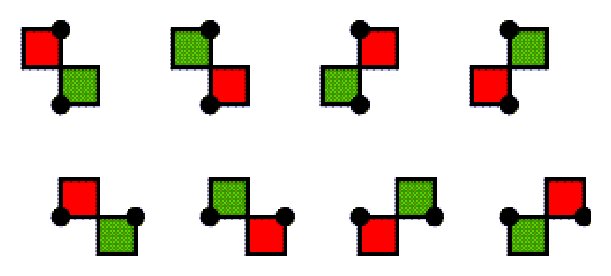
Figure 6 The new condition (ii) may be described as follows. Consider the four unit squares between two vertically or horizontally neighbouring grid points. Two of them that belong to different rows and different columns always have different colours (Figure 6). The two properties
(i) and (ii) imply that a square Liki-design
and its associated Liki-matrix are composed of cycles of alternating red
and green unit squares and of cycles of alternating 0s and 1s, respectively.
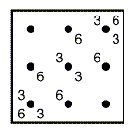
Figure 7 Figure 7 illustrates the case of the 3×3 Liki-design B. The corresponding Liki-matrix has dimensions 6×6. A question that naturally emerges is what will happen with the powers of Liki-matrices?
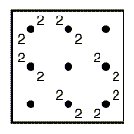
Figure 8
Figure 9
Figure 10
Figure 11 Figure 8 displays the first four powers of Liki-matrix B. The third power has the same cycle structure as the first power: the first cycle of the third power is composed of alternating 3s and 6s, the second cycle of alternating 2s and 7s and the third cycle, once again, of alternating 3s and 6s (Figure 9). The even powers do not have the same cycle structure. Their diagonals are constant and they present other cycles, like the cycle of 2s (Figure 10) of the second power. Figure 11 compares the cycle structures of the odd and even powers of the Liki-matrix B. A cycle structure of the first type I call a first order cycle structure. A cycle structure of the second type I call a second order cycle structure. The first order cycles of the odd powers of B seem to be composed of alternating numbers. In other words, these cycles have period 2. The second order cycles of the even powers of B seem to be constant. In other words, the cycles have period 1. Instead of considering powers of a Liki-design, we may consider the multiplication of Liki-designs. The following two theorems are proven in (2002b): Theorem 1: Let A and B be Liki-matrices of dimensions (2m) × (2m). AB has a second order cycle structure of period 1. Theorem 2: If A and B are Liki-matrices of dimensions (2m) × (2m), then A and B commute: AB=BA. 0 1 0 1 1 0 1 0
0 1 1 0 0 1 0 1
P
Q
1 2 2 3 3 2 2 1
1 2 2 3 3 2 2 1
PQ QP Figure 12 Figure 12 illustrates
the example of the multiplication of two 4×4
Liki-designs.
First level generalisation Now we may define square Liki-matrices in another way. Square Liki-matrices are square {0,1}-matrices of even dimensions that have a first order cycle structure; each cycle has period 2. With this redefinition, we are immediately invited to consider a first level of generalisation of Liki-matrices and their powers: matrices of even dimensions that have a first or a second order cycle structure of period 2.
Figure 13
Figure 14 Figures 13 and 14 display the general matrices of dimensions 6x6 that have a first order or a second order cycle structure of period 2. The following theorems may be proven [cf. (2002b)]: Let A and B be matrices of dimensions (2m) × (2m) that have a first order cycle structure of period 2. The product AB has a second order cycle structure of period 2. Theorem 4: Let A and B be matrices of dimensions (2m) × (2m) that have a first order cycle structure of period 2. The matrices AB and BA are symmetrical to one another: if one reflects AB about its secondary axis, one obtains BA.
A B
AB BA Figure 15 Figure 15 illustrates an example of the multiplication of two first order cycle matrices of dimensions 6×6 with period 2. Theorem 5: Let A be a matrix of dimensions (2m) × (2m) that has a first order cycle structure of period 2. A2 has a second order cycle structure of period 1. Let D and E be matrices of dimensions (2m) × (2m) that have a second order cycle structure of period 2. DE has a second order cycle structure of period 2. Theorem 7: Let D and E be matrices of dimensions (2m) × (2m) that have a second order cycle structure of period 2. D and E commute: DE=ED.
P Q
PQ = QP Figure 16 Figure 16 illustrates an example of the multiplication of two second order cycle matrices of dimensions 6×6 with cycles of period 2. Let D be a matrix of dimensions (2m) × (2m) that has a first order cycle structure of period 2. Let E be a matrix of dimensions (2m) × (2m) that has a second order cycle structure of period 2. Both DE and DE have a first order cycle structure of period 2. 84 79 75 72 68 63 72 63 79 68 84 75 68 75 63 84 72 79 84 79 75 72 68 63 79 72 84 63 75 68 63 68 72 75 79 84 63 68 72 75 79 84 75 84 68 79 63 72 72 63 79 68 84 75 68 75 63 84 72 79 AP PA Figure 17 Figure 17 illustrates an example of the multiplication of a first order and a second order cycle matrix of dimensions 6×6 with cycles of period 2. Theorem 9: Let A be a matrix of dimensions (2m) × (2m) that has a first order cycle structure of period 2. The odd powers of A have a first order cycle structure of period 2, whereas the even powers of A have a second order cycle structure of period 2. The following Table summarises the results obtained with the multiplication of matrices A and B of dimensions (2m) × (2m) that have a first or a second order cycle structure of period 2:
Multiplication table of even cycle matrices of period 2 This multiplication
table is similar to the multiplication table of negative and positive numbers.
We may call therefore matrices that have a first order cycle structure
negative cycle matrices,
and matrices that have a second order cycle structure
positive
cycle matrices.
Second level generalisation The cycle structures discussed so far have period 2. The question arises naturally if other periods are possible, and if so, what will happen. As there are 4m unit squares in each cycle of a (2m) × (2m) matrix, any period p that is a divisor of 4m may be considered. There exists no problem with the generalisation of first order cycle matrices. In the case of second order cycle matrices of period 2 we had constant diagonals, that is of period 1. If we consider those diagonals as degenerated cycles, whereby the upper and the lower parts of the cycle collapsed, their period of 1 instead of 2 is understood. This understanding makes it possible to extend the concept of a second order cycle structure in the following way. We will say that a (2m) × (2m) matrix has a second order cycle structure of period p if all its second order cycles have period p, i.e. both the normal second order cycles and the two diagonals as degenerated cycles have period p.
E F Figure 18
EF FE Figure 19 Figure 18 presents two matrices of dimensions 6×6 that have, in the extended sense, a second order cycle structure of period 4. Their products have also a second order cycle structure of period 4 (see Figure 19). The general form of a second order cycle matrix of dimensions 6×6 with period 4 is abbaab. The following generalisations of theorems 3, 6 and 8 may be proven, consistent with the multiplication table: Theorem 3: Let A and B be matrices of dimensions (2m) × (2m) that have a first order cycle structure of period p. The product AB has a second order cycle structure of period p. Theorem 6: Let A and B be matrices of dimensions (2m) × (2m) that have a second order cycle structure of period p. The product AB has a second order cycle structure of period p. Theorem 8: Let A be
a matrix of dimensions (2m) × (2m)
that has a first order cycle structure of period p. Let B
be a matrix of dimensions (2m) × (2m)
that has a second order cycle structure of period p. Both products
AB and BA have a first order cycle structure of period p.
Third level of generalisation The dimensions of the matrices considered so far are (2m) × (2m). We may call the matrices therefore even cycle matrices. We may ask if it is possible to define odd cycle matrices.
Figure 20 The extension of first order and second order cycle structures to square matrices of odd dimensions should, if possible, be consistent with the multiplication of even cycle matrices. It comes out that this is indeed possible. When the principal diagonal may be considered a collapsed cycle of certain period, we may call the odd cycle structure a positive or a second order cycle structure. When the secondary diagonal may be considered a collapsed cycle, we may call the odd cycle structure a negative or first order cycle structure. Figure 20 illustrates the first and the second order cycle structures of dimensions 7×7. In the case of odd matrices of dimensions (2m+1) × (2m+1) the period p has to be a divisor of 2(2m+1).
A B First order cycle structure of dimensions 9×9 and period 6
AB BA Second order cycle structure of dimensions 9×9 and period 6 Figure 21 Figure 21 presents some experimentation with the multiplication of 9x9 matrices that have a first order cycle structure of period 6. The products have a second order cycle structure of period 6. The reader is invited to do some further experimentation. The following theorems may be proven: Theorem 3: If A and B are matrices of dimensions (2m+1) × (2m+1) that have a first order cycle structure of period p, then AB has a second order cycle structure of period p. Theorem 6: If A and B are matrices of dimensions (2m+1) × (2m+1) that have a second order cycle structure of period p, then AB also has a second order cycle structure of period p. Theorem 8: Let A and B be matrices of dimensions (2m+1) × (2m+1) that have a first order cycle structure and second order cycle structure of period p, respectively, then AB and BA have a first order cycle structure of period p. Once again, the same multiplication table holds. An immediate consequence of the previous theorems is the following: Theorem 9: If A is a
matrix of dimensions (2m+1) × (2m+1)
that has a first order cycle structure of period p, then the even
powers of A have a second order cycle structure of period p
and the odd powers of A have a first order cycle structure of period
p.
Conclusion Cycle matrices constitute
a generalisation of Liki-matrices. The paper shows the beauty of the reproduction
of both negative and positive cycle structures in the multiplication of
both even and odd cycle matrices of period p. The two cycle structures
may be considered as a new type of symmetry for square matrices.
General multiplication table of cycle matrices
of period p
Bibliography of books and papers by Paulus Gerdes related to Lunda-designs. (1990) On ethnomathematical research and symmetry, Symmetry: Culture and Science, Budapest, 1(2), 154-170 (1993-4) Geometria Sona, Universidade Pedagógica, Maputo (3 volumes) (1995) Une tradition géométrique en Afrique Les dessins sur le sable, L'Harmattan, Paris (3 volumes) (1996) Lunda Geometry Designs, Polyominoes, Patterns, Symmetries, Universidade Pedagógica, Maputo (1997) Ethnomathematik dargestellt am Beispiel der Sona Geometrie, Spektrum Verlag, Heidelberg (1997a) On mirror curves and Lunda-designs, Computers and Graphics, An international journal of systems & applications in computer graphics, 21(3), 371-378 (1999) Geometry from Africa: Mathematical and Educational Explorations, The Mathematical Association of America, Washington DC (1999a) On the geometry of Celtic knots and their Lunda-designs, Mathematics in School, 28(3), 29-33 (1999b) On Lunda-designs and some of their symmetries, Visual Mathematics, 1(1), (http://members.tripod.com/vismath/paulus/) (2000) On Lunda-designs and the construction of associated magic squares of order 4p, The College Mathematics Journal, 31(3), 182-188 (2001) Symmetrical Explorations Inspired by the Study of African Cultural Activities, in: T. Laurent & I. Hargittai (Eds.) Symmetry 2000, Portland Press, London (in press) (2002) Variations on Lunda-designs, in: M. Emmer (Ed.), Matematica e Cultura 2002, Springer-Verlag, Milano (in press) (2002a) Lunda Symmetry where Geometry meets Art, in: M. Emmer (Ed.), The Visual Mind 2, MIT Press, Boston (in press) (2002b) The
beautiful geometry and linear algebra of Lunda-designs (book manuscript),
204 pp
|