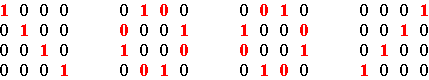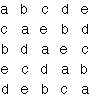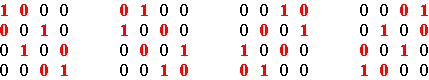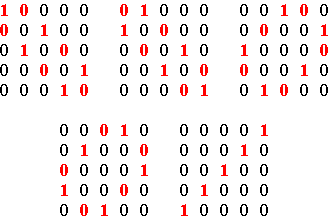|
On the representation and multiplication of basic alternating cycle matrices
Dr. Paulus Gerdes
Abstract In the
following paper the circular representation of basic positive and basic
negative alternating cycle matrices is determined. This representation
enables the calculation of the multiplication tables of basic positive
and basic negative alternating cycle matrices. Surprisingly, the associated
matrices of these multiplication tables are alternating cycle matrices
themselves. Several further properties are derived. The multiplication
of positive and negative alternating cycle matrices follows the rule of
signs of the multiplication of positive and negative numbers. The multiplication
of positive alternating cycle matrices is commutative. The multiplication
of negative alternating cycle matrices is symmetrical.
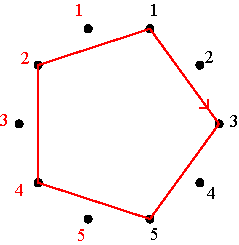
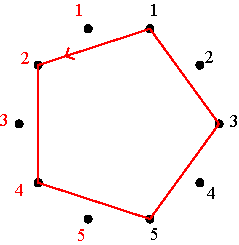
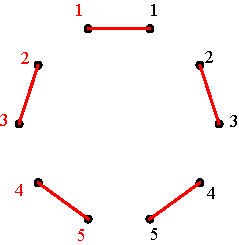
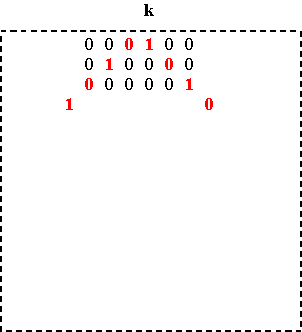
Basic alternating cycle matrices Any positive alternating cycle matrix of dimensions m × m is a linear combination of the basic positive alternating cycle matrices P1, P2, …, Pm, where P1 = I, the identity matrix, Pk (k = 2, .., m-1) the matrix that has 0’s on its principal diagonal, 0’s on its secondary diagonal if m is an even number, and all positive cycles are composed of only 0’s with the exception of one positive alternating (0,1)-cycle that passes through the k-th element of the first row, such that Pk(1,k) = 1. If m is an even number, then Pm is the matrix that has 1’s on its secondary diagonal and 0’s elsewhere. If m is an odd number, then Pm is defined like Pk before. Figures 1 and 2 illustrate the basic positive alternating cycle matrices in the cases m=4 and m=5.
The basic positive alternating cycle matrices (m=4)
The basic positive alternating cycle matrices (m=5) Figure 2 The positive alternating cycle matrix
P of dimensions 5×5 with (a b c d e) as its first row
(Figure 3) may be written as: P = aP1
+ bP2 + cP3 + dP4
+ eP5.
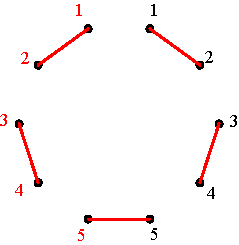
Matrix P Figure 3 Similarly, any negative alternating cycle matrix of dimensions m × m is a linear combination of the basic negative alternating cycle matrices N1, N2, …, Nm, where Nk (k = 1, .., m-1) is the matrix that has 0’s on its secondary diagonal if m is an odd number, and all its negative cycles are composed of only 0’s with the exception of one negative alternating (0,1)-cycle that passes through the k-th element of the first row, such that Nk(1,k) = 1. If m is an even number, then Nm is defined like Nk before. If m is an odd number, then Nm is the matrix that has 1’s on its secondary diagonal and 0’s elsewhere. Figures 4 and 5
illustrate the basic negative alternating cycle matrices in the cases m=4
and m=5.
The basic negative alternating cycle matrices (m=4)
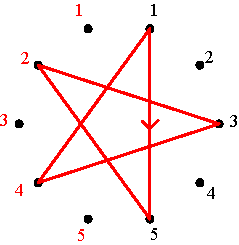
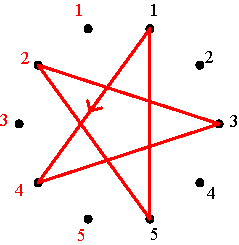
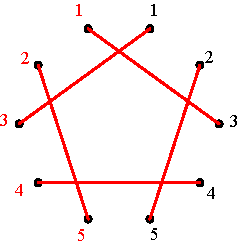
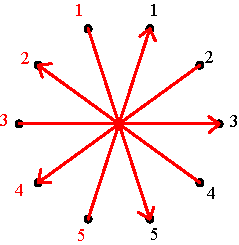
The basic negative alternating cycle matrices (m=5) Figure 5 Basic positive and negative alternating cycle matrices as permutation matrices The basic positive and negative alternating cycle matrices of dimensions m x m constitute a particular class of permutation matrices. The elements of this class admit a circular representation. Consider 2m points equally spaced around a circle, numbered clockwise 1, 2, …, m, m, m-1, …, 2, 1, being the first m points on the right side and the other m points on the left side. The circular representation of a basic alternating cycle matrix consists of a directed graph joining points around the circle. Figure 6 displays
the circular representation of the basic positive alternating cycle matrices
P2, P3, P4 and P5
in the case m=5. The representation corresponds to the cycle notation
of the respective permutations: (1 3 5 4 2) for P2, (1
2 4 5 3) for P3, (1 5 2 3 4) for P4,
and (1 4 3 2 5) for P5. In the circular representation
one advances in the case of P2, each time clockwise 2
points: from the right 1-point to the right 3-point, etc. In the case of
P3, one advances each time anticlockwise 2 points: from
the right 1-point to the left 2-point, etc. In the case of P4,
one advances each time clockwise 4 points. In the case of P5,
one advances each time anticlockwise 4 points.
(a)
(b)
(c)
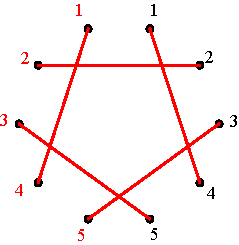
(d) Circular representation of P2, P3, P4 and P5 in the case m=5 Figure 6 Figure 7 displays the circular representation of the basic negative alternating cycle matrices N1, N2, N3, N4 and N5 in the case m=5. Once again the representation corresponds to the cycle notation of the respective permutations: (2 3) (4 5) for N1 , (1 2) (3 4) for N2, (1 3) (2 5) for N3, (1 4)(3 5) for N4, and (1 5)(2 4) for N5. Either one starts at the 1-point at the left, as is the case of N1, N3 and N5, or at the 1-point at the right, as is the case of N2 and N4, and advances clockwise.
(a)
(b)
(c)
(d)
(e) Circular representation of N1, N2, N3, N4 and N5 in the case m=5 Figure 7 Table 1 summarizes the structure of the circular representations of the basic positive and the basic negative alternating cycle matrices, where C2 refers to advancing clockwise each time two points; A4 means advancing each time anticlockwise 4 points. L5 means starting at the 1-point at the left side and advancing clockwise each time 5 points; R3 means starting at the 1-point at the right side and advancing clockwise each time 3 points, etc.
Basic alternating cycle matrices and structure of corresponding circular representations (m = 5) Table 1 Let us now analyse for any m the relationship between basic positive and negative alternating cycle matrices and the structure of their circular representation. We may extrapolate that the following proposition is valid: * The circular representation of Nk is R(k-1), if k is an even number (1 < k £ m), and Lk, if k is an odd number. Let us prove the first case: if k
is an odd number (1 < k £
m), then the circular representation
of Pk has as structure A(k-1). As k
is odd, there exists a natural number
s such that k = 2s+1.
The s-th positive cycle passes through the first row in (1, k-1)
and (1,k). According to the definition of Pk,
it has a 0 in (1, k-1) and a 1 in (1,k) (Figure 8).
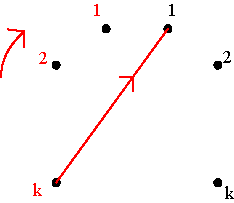
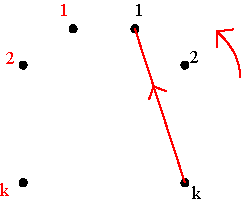
Figure 8 As a permutation matrix, Pk transforms the k-th element into the 1st. This leads to two possibilities for the circular representation, as Figure 9 illustrates, either there is an arrow from the k-point on the left to the right 1-point, or there is an arrow from the right k-point to the right 1-point. The first possibility would correspond to Ck, the second to A(k-1).
Ck A(k-1) Two possibilities Figure 9 Pk transforms the (k-2)-th element into the 2nd element and/or the (k+2)-th element into the 3rd element (see Figure 8). In the first scenario this would correspond to clockwise advances of (k-1) points, what is not compatible with Ck. In the second scenario, it would correspond to anticlockwise advances of k-1 points from the (k-2)-point on the right to the 2-point on the left, and from the (k+2)-point on the right to the 3-point on the right side, both in agreement with A(k-1). Thus A(k-1) is the only possible structure for the circular representation of Pk. Remains to be analysed if it really describes the whole transformation. Consider first the odd elements. On the one hand Pk transforms the (k+2t)-th element into the (2t+1)-th element (cf. Figure 8), if k+2t £ m. Thus, the arrow goes from the (k+2t)-point on the right side to the (2t+1)-point on the same side, advancing anticlockwise (k+2t)-(2t+1), that is k-1 points. On the other hand Pk transforms the (k-2t)-th element into (2t)-th element, if 1 £ k-2t. Therefore, the arrow goes from the (k-2t)-point on the right side to the 2t-point on the left side, advancing anticlockwise ((k-2t)-1)+2t, that is k-1 points. Consider now the even elements. We have to distinguish two different situations: 2k £ m and 2k > m (see Figure 10).
Cycle form in the cases 2k £ m and 2k > m Figure 10 In the first case 2k £ m, firstly, Pk transforms the (k-1-2t)-th element into the [2(k-1)-2t]-th element, where 1 £ k-1-2t. In other words, the arrow goes from the (k-1-2t)-point on the left to the [2(k-1)-2t]-point on the left side, corresponding to an anticlockwise advance of [2(k-1)-2t] - (k-1-2t) or k-1 points, in agreement with the predicted structure A(k-1). Secondly Pk transforms the (k+1+2t)-th element into the (2k+2t)-th element, where k+1+2t £ m-k. This means that the arrow goes from (k+1+2t)-point on the left to the (2k+2t)-th on the same side, once again corresponding to an anticlockwise advance of k-1 points. Thirdly Pk transforms the (m-k+3+2t)-th element into the (m-1-2t)-th element, if k > 3+2t and if m is an even number. This means the arrow goes from the (m-k+3+2t)-point on the left side to the (m-1-2t)-point on the right side, corresponding to an anticlockwise rotation of (k-3-2t) + 1+ (1+2t), that is, of k-1 points. And finally Pk transforms the (m-k+2+2t)-th element into the (m-2t)-th element, if k > 2+2t and if m is an odd number. In other words, the arrow goes from the (m-k+2+2t)-point on the left side to the (m-2t)-point on the right side, corresponding to an anticlockwise rotation of (k-2-2t) + 1+ (2t), that is, of k-1 points. In the second case 2k > m, a similar reasoning leads to the same result. We may conclude that, if k is an odd number (1 < k £ m), then the circular representation of Pk has the structure A(k-1). The other three parts of the theorem may be proven analogously. Theorem 1 * The circular representation of Nk
is R(k-1), if k is an even number (1 < k
£
m), and Lk, if k is an odd number.
Let us now calculate the multiplication tables of the basic positive and negative alternating cycle matrices of dimensions m × m. 1) Positive times positive (multiplication table 1) Firstly we shall consider the products of basic positive alternating cycle matrices of dimensions m × m: Pu × Pv = ? Depending on u and v being even or odd numbers, we have to distinguish four cases. Case 1: u and v are even numbers. Otherwise, if u+v > m, we have [C(u+v)] = [A(2m-(u+v))] = P(2m-u-v+1). Otherwise, if u < v, we have Pu × Pv = [Cu + A(v-1)] = [A(v-1-u)] = [A(v-u-1)] = P(v-u). Otherwise, if u < v, we have Pu × Pv = [A(u-1) + Cv] = [C(v-u+1)] = P(v-u+1). Otherwise, if u+v-1 >
m, we have Pu × Pv
= [A(u+v-2)] = [C(2m-(u+v-2))]
= P(2m-u-v+2).
Secondly we shall consider the products of basic positive alternating cycle matrices of dimensions m × m times basic negative alternating cycle matrices of the same dimensions: Pu × Nv = ? Depending on u and v being even or odd numbers, we have to distinguish four cases. Case 1: u and v are even numbers. Otherwise, if u > v, we have Pu × Nv = [Cu + R(v-1)] = [R(v-(u+1))] = N(v-u). Otherwise, if u+v > m, we have Pu × Nv = [R(2m-u-v)] = N(2m-u-v+1). Otherwise, if u+v-1 > m, we have Pu × Nv = [R(u+v-2)] = [L(2m-u-v+2)] = N(2m-u-v+2). Otherwise, if u > v,
we have Pu × Nv = [A(u-1)
+ L(v)] = [L(v-(u-1)]= N(v-u+1).
Thirdly we shall consider the products of basic negative alternating cycle matrices of dimensions m × m times basic positive alternating cycle matrices of the same dimensions: Nu × Pv = ? We have to distinguish four cases. Case 1: u and v are even numbers. Otherwise, if u+v > m, we have Nu × Pv = [R(u+v-1)] = [L(2m-u-v+1)] = N(2m-u-v+1). Otherwise, if v < u, we have Nu × Pv = [R(u-v)] = N(u-v+1). Otherwise, if u > v, we have Nu × Pv = [Lu + Cv] = [L(u-v)] = N(u-v). Otherwise, if u+v-1 >
m, we have Nu × Pv = [Lu
+ A(v-1)] = [R(2m-u-v+1)] = N(2m-u-v+2).
Fourthly we have to consider the products of basic negative alternating cycle matrices of dimensions m × m: Nu × Nv = ? Once again we have to distinguish four cases. Case 1: u and v are even numbers. Otherwise, if u > v, we have Nu × Nv = [C(v-u)] = P(v-u). Otherwise, if u+v > m, we have Nu × Nv = [A(u+v-1)] = [C(2m-u-v+1)] = P(2m-u-v+1). Otherwise, if u+v-1 > m, we have Nu × Nv = [A(2m-u-v+1)] = P(2m-u-v+2). Otherwise, if u £
v, we have Nu × Nv = [A(v-u)]
= P(v-u+1).
Comparing case by case the results of the multiplication of Pu × Pv (multiplication table 1) with those of the multiplication of Nu × Pv (multiplication table 3), we see that Pu × Pv = Ps if and only if Nu × Pv = Ns. In other words, the respective multiplication
tables have the same associated matrix of indices. Figure
11 illustrates, the cases m=5 and m=6.
m=5
m=6 Multiplication tables and associated matrix Figure 11 Moreover and surprisingly, the associated matrix itself is also a negative alternating cycle matrix. We found the following theorem. Theorem 2 Comparing case by case the results of the multiplication of Pu × Nv (multiplication table 2) with those of the multiplication of Nu × Nv (multiplication table 4), we see that Pu × Nv = Ns if and only if Nu × Nv = Ps. In other words, the respective multiplication
tables have the same associated matrix of indices. Figure
12 illustrates, the cases m=5 and m=6.
m=5
m=6 Multiplication tables and associated matrix Figure 12 The structure of the associated matrix is that of a positive alternating cycle matrix. Thus, we arrive at the following theorem. Theorem 3 As positive alternating cycle matrices are linear combinations of basic positive alternating cycle matrices and as negative alternating cycle matrices are linear combinations of basic negative alternating cycle matrices, the multiplication tables imply the following theorem: Theorem 4
Figure 13 From multiplication table 1, it follows immediately that Pu × Pv = Pv × Pu for all u and v. In other words, the multiplication of basic positive alternating cycle matrices is commutative. Supposing the matrix elements of positive alternating cycle matrices belong to a field, we find that the following theorem is true. Theorem 5 In agreement with the circular representation of basic positive alternating cycles (Theorem 1) and the subsequent multiplication table 1, we have for basic positive alternating cycle matrices several other properties, like P2P3 = P4P5 = P6P7 = … = I, P1P2P3…..P(2n+1) = I, (Ps)m = I. From multiplication table 4, it follows that the matrices Nu × Nv and Nv × Nu are symmetrical in the sense that a reflection in the principal diagonal of the first matrix transforms it into the second matrix. In the other words, the second matrix is the transposed matrix of the first one: Nu × Nv = [Nv × Nu]’ Supposing the matrix elements of negative alternating cycle matrices belong to a field, we find that the following theorem is true. Theorem 6
References
on cycle matrices:
Gerdes, Paulus (2002a), From Liki-designs to cycle matrices: The discovery of attractive new symmetries, Visual Mathematics, Vol. 4, No. 1, (http://members.tripod.com/vismath7/gerd/) Gerdes, Paulus (2002b), Helix matrices, Visual Mathematics, Vol. 4, No. 2, June 2002 (http://members.tripod.com/vismath8/gerdhel/hel.htm) Gerdes, Paulus (2002c), Cylinder matrices, Visual Mathematics, Vol. 4, No. 2, June 2002 (http://members.tripod.com/vismath8/gerdcyl/cyl1.htm) Gerdes, Paulus (2004), Aventuras no Mundo das Matrizes [Adventures in the World of Matrices], book manuscript Gerdes, Paulus (2005), Mathematical research inspired by African cultural practices: The example of mirror curves, Lunda-designs and related concepts, in: Giandomenico Sica (Ed.), What Mathematics from Africa?, Polimetrica, Milano, 2005, 29-47. Gerdes, Paulus (2006), Symmetries of alternating cycle matrices, paper submitted to Visual Mathematics.
|