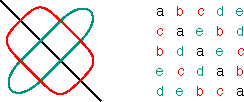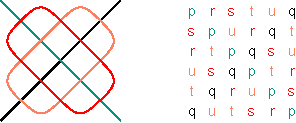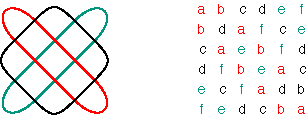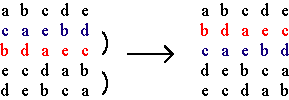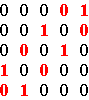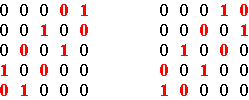|
Symmetries of alternating cycle matrices
Dr. Paulus Gerdes Introduction The context in which cycle matrices were discovered and some of their basic symmetry properties are explained in Gerdes (2002a and 2005). The book Adventures in the World of Matrices (Gerdes 2004) presents an introduction to alternating cycle matrices and cycle matrices of any period p. The papers Gerdes (2002b and c) introduce helix and cylinder matrices and explore some of their relationships with cycle matrices. In the following paper some further symmetry properties
of alternating cycle matrices will be presented. The paper concludes with
a geometrical interpretation of a class of permutation matrices that are
simultaneously alternating cycle matrices. It is hoped that the article
may underscore some of the beautiful symmetric properties of cycle matrices
and may stimulate further exploration.
Definition and generalities Alternating cycle matrices constitute a particular class of square matrices. If m is an odd number (m = 2n+1), a matrix of dimensions m × m is called a positive alternating cycle matrix if all the elements on its principal diagonal are equal and if it is composed of n cycles of alternating numbers. Figure 1 illustrates the structure and general form of a positive alternating cycle matrix of dimensions 5×5.
Structure and general form of a positive alternating cycle matrix of dimensions 5×5 Figure 1 If m is an odd number (m = 2n+1), a matrix of dimensions m × m is called a negative alternating cycle matrix if all the elements on its secondary diagonal are equal and if it is composed of n cycles of alternating numbers. Figure 2 illustrates the structure and general form of a negative alternating cycle matrix of dimensions 5×5. 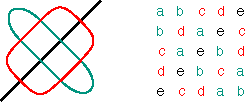
Structure and general form of a negative alternating cycle matrix of dimensions 5×5 Figure 2 If m is an even number (m = 2n), a matrix of dimensions m × m is called a positive alternating cycle matrix if each of its diagonals is constant and if it is furthermore composed of n-1 cycles of alternating numbers. Figure 3 illustrates the structure and general form of a positive alternating cycle matrix of dimensions 6×6.
Structure and general form of a positive alternating cycle matrix of dimensions 6×6 Figure 3 If m is an even number (m = 2n), a matrix of dimensions m × m is called a negative alternating cycle matrix if it is composed of n cycles of alternating numbers. Figure 4 illustrates the structure and general form of a negative alternating cycle matrix of dimensions 6×6.
Structure and general form of a negative alternating cycle matrix of dimensions 6×6 Figure 4 The adjectives ‘positive’ and ‘negative’ are justified by the fact that the multiplication of positive and negative alternating cycles satisfies the same multiplication rules as positive and negative numbers: + × + = +, + × – = –, – × + = –, and – × – = +. Moreover, if A and B are two positive alternating cycle matrices of the same dimensions, then AB = BA. If C and D are two negative alternating cycle matrices of the same dimensions, then CD and DC are mutually symmetric: DC is the transposed matrix of CD. In the following some further symmetries of alternating
cycle matrices will be presented.
Inverse matrices The inverse matrices of non-singular
alternating cycle matrices are also alternating cycle matrices.
Let A be a non-singular positive alternating cycle matrix of dimensions m × m. Let r = (b1, …, bm) be the first row of B = A-1. We may construct the unique positive alternating cycle matrix C that has r as its first row. On its turn CA is a positive alternating cycle matrix, being its first row equal to the first row of BA. As B = A-1, we have BA = A-1A = I, where I represents the identity matrix of dimensions m ×m. The first row of BA is (1, 0, …, 0). By consequence, the first row of CA is (1, 0, …, 0). As CA is a positive alternating cycle matrix, its principal diagonal is composed of 1’s and its cycles composed of 0’s. It follows that CA = I, and thus C is the inverse matrix of A: C = B = A-1. As C is by construction a positive alternating cycle matrix, we have proven that the inverse matrix of a non-singular positive alternating cycle matrix is a positive alternating cycle matrix itself. The proof for the case that A is a non-singular
negative alternating cycle matrix is analogous to the proof given.
Determinants Let P be any positive alternating cycle matrix of dimensions m × m (m = 3, 4, 5, ….). Let N be the negative alternating cycle matrix that has the same first row as P. For the determinants of P and N, we have By interchanging the 2nd and the 3rd row, the 4th and the 5th row, …, and the (2n)th and the (2n+1)th row, matrix P is transformed into matrix N. Interchanging two rows of a matrix implies changing the sign of the corresponding determinant. As we have a total of n interchanges, it follows that det P = (-1)n det N. Figure 5 illustrates the cases m=5 and m=6.
(a) m = 5, n = 2; (b) m = 6, n = 2 Figure 5 Two (positive or negative) alternating cycle matrices A and B may be called equivalent, if each row of A is a row of B, and vice versa. By interchanging several pairs of rows, matrix A can be transformed into any equivalent matrix B. By consequence, we have If A and B are equivalent alternating cycle matrices, then |det A| = |det B|. Let A be a positive alternating cycle matrix of dimensions m × m. If we construct another positive alternating cycle matrix B that has the first row of A as one of its rows, what can be said about B? Let us consider an example. F is a positive alternating cycle matrix of dimensions 5×5. We construct a positive alternating cycle matrix G such that the first row of F becomes the fourth row of G (see Figure 6). 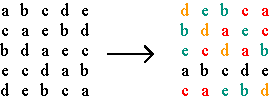
Transformation of matrix F in matrix G Figure 6 In this example we see that all rows of F appear as rows of G, and vice versa. The same holds for the columns of F and G. How can we explain this phenomenon? Let V4 be the positive alternating cycle matrix of dimensions 5×5 that has 0’s on the principal diagonal, one cycle of 0’s and one alternating cycle of 0’s and 1’s such that the first element of its 4th row is 1 (Figure 7). V4 is a permutation matrix, i.e. a square matrix whose elements in any row (or any column) are all zero, except for one element equal to unity.
Permutation matrix V4 Figure 7 Let us multiply the matrices V4 and F. As the 4th row of V4 is (1, 0, 0, 0, 0), the 4th row of V4F is (a, b, c, d, e), that is the first row of F. As V4 and F are positive alternating cycle matrices, the product is also a positive alternating cycle matrix. There exists only one positive alternating cycle matrix that has (a, b, c, d, e) as its 4th row. It follows that V4F = G. Similarly FV4 = G. We may conclude that F and G are equivalent. Based on this and similar experiences we may conjecture the following generalisation: Let A be a positive alternating cycle matrix of dimensions m × m. If B is defined as the positive alternating cycle matrix that has the first row of A as its pth row (p = 2, …, m), then A and B are equivalent alternating cycle matrices. Let Vp be the positive alternating cycle matrix of dimensions m × m whose elements in the first column are all zero, except for the first element of the pth row that is equal to unity. By consequence, Vp is a permutation matrix and its pth row is (1, 0, …, 0). Vp A is a positive alternating cycle matrix and its pth row is equal to the first row of matrix A. As there exists only one positive alternating cycle matrix that has the first row of A as its pth row, it follows immediately that Vp A = B, and all rows of B are rows of A. We conclude that A and B are equivalent alternating cycle matrices. Before considering in more detail the properties of the particular permutation matrices Vp, let us analyse the relationship between the inverse matrices of A and B in the case that A and B are non-singular. We may conjecture If A and B are equivalent non-singular alternating cycle matrices, then A-1 and B-1 are equivalent alternating cycle matrices. We have A Vp = Vp A = B, for a certain p = 2, …, m. The inverse of Vp is another matrix of the same type Vq (cf. Gerdes 2005). We have B-1 = (Vp A)-1 = A-1 (Vp)-1 = A-1Vq and B-1 = (A Vp)-1 = (Vp)-1 A-1 = Vq A-1. Thus A-1 Vq = Vq
A-1 = B-1. In other words, the matrices
A-1
and B-1 are equivalent positive alternating cycle matrices.
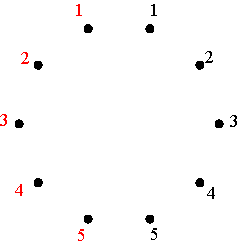
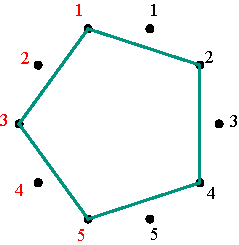
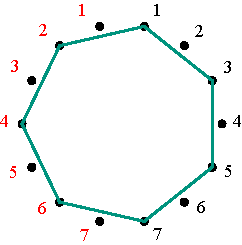
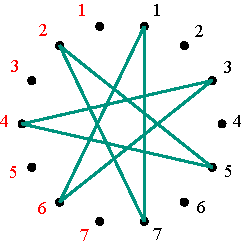
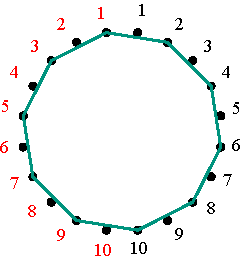
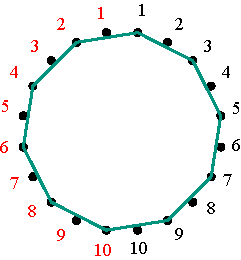
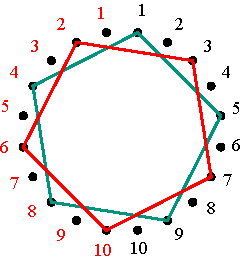
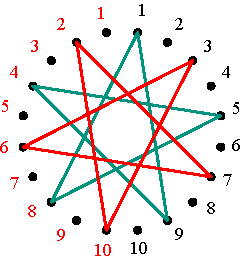
Permutations The matrices Vp constitute a particular class of permutation matrices: the permutation matrices that are simultaneously positive alternating cycle matrices. Let us observe the example V4 when m = 5 (Figure 7). Multiplying a positive alternating cycle matrix of dimensions 5×5 by V4, transforms the first row of A into the 4th row of the new matrix B (= A V4), the 4th row of A becomes the 3rd of B, the 3rd row of A becomes the 2nd of of B, the 2nd row of A becomes the 5th of B, and the 5th row of A becomes the 1st of B. In other words, the cycle notation for the permutation of the rows is (1 4 3 2 5). Similarly, the matrices V2, V3, and V5 of dimensions 5×5, correspond to (1 2 4 5 3), (1 3 5 4 2), and (1 5 2 3 4). How can we understand and interpret the particular sequence of the numbers 1 to 5 in the cycle notation of these permutations? In general, any cycle of a cycle matrix passes exactly twice through each row. In the particular case of V4, the non-zero cycle passes exactly twice to each of the five rows. Correspondingly, let us mark 10 dots at equal intervals around a circle and number these dots twice, on the left and on the right, from 1 to 5, as illustrated in Figure 8.
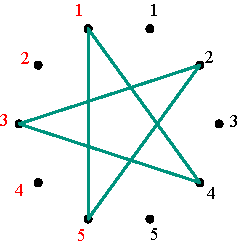
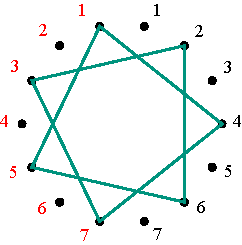
Marking and numbering of ten dots Figure 8 The permutation (1 4 3 2 5) can now be represented by a polygon: starting with the 1-dot on the left side, advancing clockwise four dots one arrives at the 4-dot on the right side (draw the corresponding segment 1-4); advancing another four dots one arrives at 3-dot on the left side (draw the corresponding segment 4-3); advancing once more four dots, one arrives at the 2-dot on the right (segment 3-2), and then at the 5-dot on the left (drawing the segment 2-5) and finally by advancing four more dots one returns to the initial 1-dot on the left (Figure 9). The final representation of the permutation (1 4 3 2 5) is that of a regular pentagram.
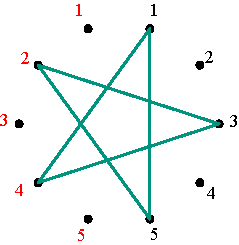
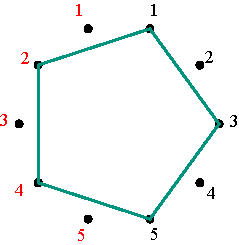
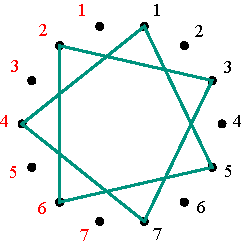
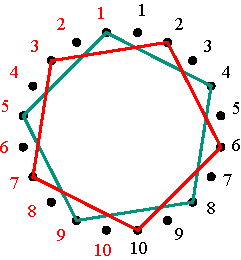
Regular pentagram corresponding to permutation (1 4 3 2 5) Figure 9 The inverse permutation of (1 4 3 2 5) is (5 2 3 4 1) that may be written as (1 5 2 3 4), and its representation is the vertical mirror image of the first (Figure 10).
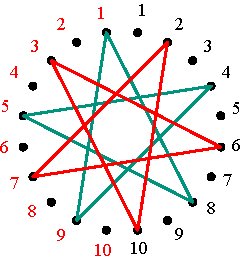
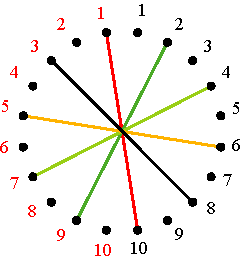
Polygonal-circle representation of the permutation (1 5 2 3 4) Figure 10 On the one hand, the mutually inverse permutations (1 4 3 2 5) and (1 5 2 3 4) correspond to the positive alternating cycle matrices V4 and V5 with V4V5 = V5 V4 = I. At the same time these matrices are mutually symmetrical: a reflection in the principal diagonal of V4 transforms V4 into V5, and vice versa (Figure 11). In other words, V5 is the transposed matrix of V4: V5 = (V4)T. On the other hand, the polygonal-circle representations of these matrices (Figures 8 and 10) are mutually symmetrical too.
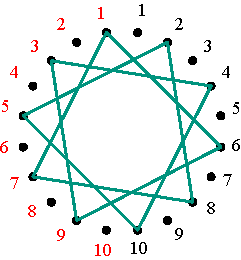
Matrices V4 and V5 when m = 5 Figure 11 The sum V4 + V5 is a positive cycle matrix of period 1 (all cycles are constant), with two axes of symmetry. Similarly, the mutual inverse permutations (1 2 4 5 3) and (1 3 5 4 2), corresponding to V2 and V3, can be represented by regular pentagons (Figure 12).
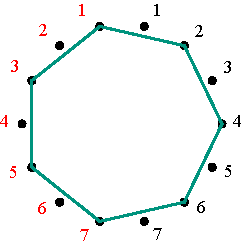
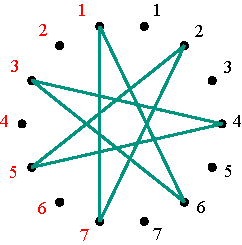
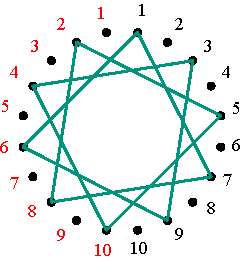
Symmetrical representations of the permutations (1 2 4 5 3) and (1 3 5 4 2) Figure 12 Figures 13 and 14 illustrate the polygonal-circle representations of permutation matrices that are positive alternating cycle matrices in the cases m=7 and m=10.
(a) (1 2 4 6 7 5 3); (b) (1 3 5 7
6 4 2); (c) (1 4 7 3 2 6 5);
The six polygonal-circle representations of permutation matrices in the case m=7
The nine polygonal-circle representations of permutation matrices in the case m=10 Figure 14 We are now in a position to extrapolate and to formulate a general conjecture. Its proof follows directly from the understanding of the reflection of the branches of any alternating cycle in the sides of the square circumscribed to the matrix. The theorem may be formulated as follows: Let A and B be two equivalent positive alternating
cycle matrices of dimensions m × m, and let Vj be the
simultaneously permutation and positive alternating cycle matrix that transforms
A into B. Consider 2m dots equally spaced around a circle, numbered clockwise
1, 2, …, m, m, m-1, …, 2,
1, being the first m dots on the right side and the other m dots
on the left side. The polygonal-circle representation of Vj
is characterised by or may be described by the following construction steps:
(2) If j is an odd number, start at the right 1-dot and advance each time j-1 dots, until returning to the left 1-dot and thus closing the polygonal line; (3) If the closed polygonal line has m vertices,
stop. If the closed polygonal line has s vertices, where s is a divisor
of m (let us say m = st), then rotate the closed polygonal line about an
angle of (360o / t) around the circle centre and copy it. Repeat
this process t-1 times.
References
Gerdes, Paulus (2002a), From Liki-designs to cycle matrices: The discovery of attractive new symmetries, Visual Mathematics, Vol. 4, No. 1, (http://members.tripod.com/vismath7/gerd/) Gerdes, Paulus (2002b), Helix matrices, Visual Mathematics, Vol. 4, No. 2, June 2002 (http://members.tripod.com/vismath8/gerdhel/hel.htm) Gerdes, Paulus (2002c), Cylinder matrices, Visual Mathematics, Vol. 4, No. 2, June 2002 (http://members.tripod.com/vismath8/gerdcyl/cyl1.htm) Gerdes, Paulus (2004), Aventuras no Mundo das Matrizes [Adventures in the World of Matrices], book manuscript Gerdes, Paulus (2005), Mathematical research
inspired by African cultural practices: The example of mirror curves, Lunda-designs
and related concepts, in: Giandomenico Sica (Ed.), What Mathematics
from Africa?, Polimetrica, Milano, 2005, 29-47.
|