|
Paulus Gerdes Mozambican Ethnomathematics
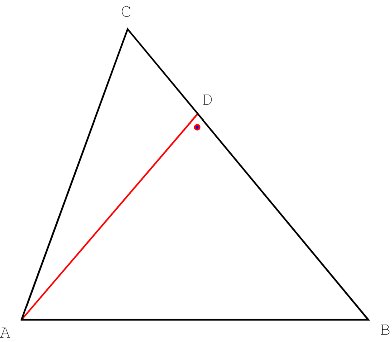
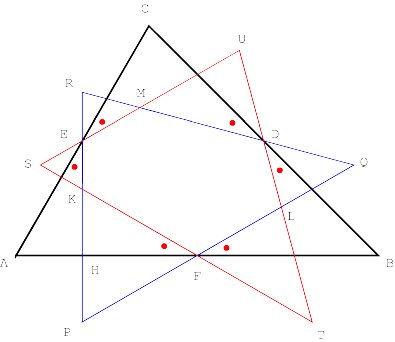
Introducing oblique altitudes Consider any triangle ABC. The line through a vertex perpendicular to the opposite side is called an altitude. According to a classical theorem of plane geometry the three altitudes of ABC are concurrent. The common point of the three altitudes is called the orthocentre of the triangle. Now let us consider any angle j . We will call a line through a vertex a j-altitude if it forms an angle equal to j with the opposite side (Figure 1).
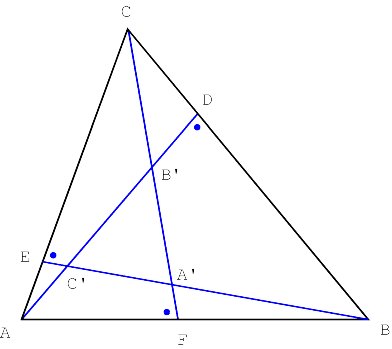
Properties of oblique altitudes The three j -altitudes AD, BE and CF have the same orientation in the sense that ÐADB = ÐBEC = ÐCFA = j . Their intersection forms a triangle ABC that is similar to triangle ABC (Figure 2).
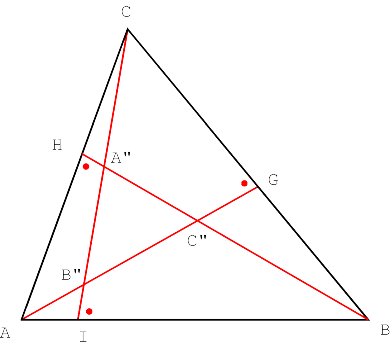
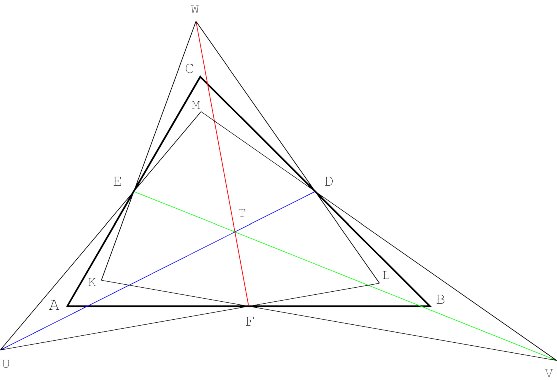
The other three j -altitudes AG, BH and CI have the opposite orientation, i.e. Ð AGC = Ð BHA = Ð CIB = j . Their intersection creates the triangle A"B"C" also similar to triangle ABC (Figure 3).
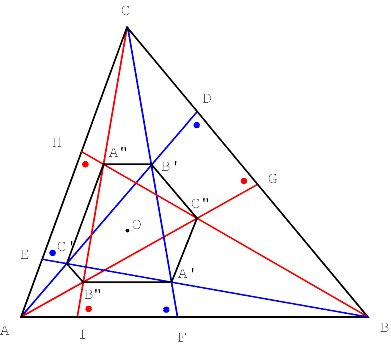
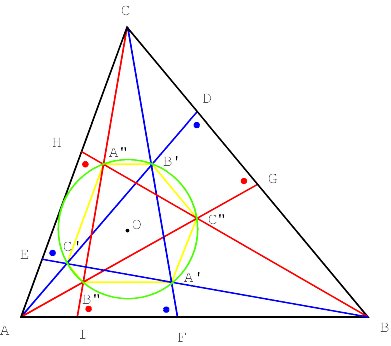
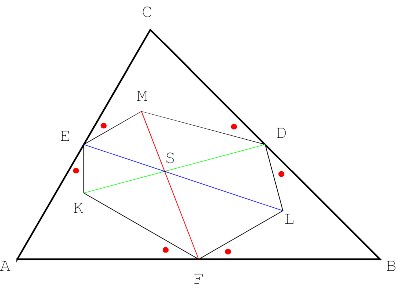
Moreover, the triangles ABC and A"B"C" are congruent [Appendix 1]. The isosceles triangles ADG, BEH and CFI are obviously similar. The opposite sides of the hexagon AC"BA"CB" are parallel (Figure 4).
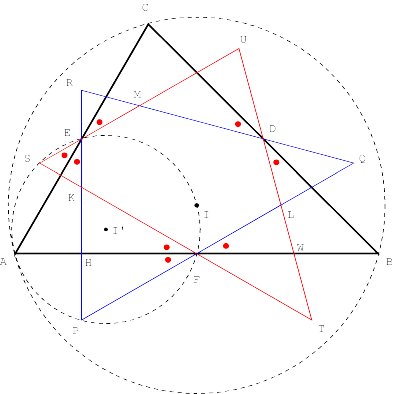
Surprisingly, the vertices of the hexagon lie on a circle and its centre is the orthocentre of ABC (Figure 5) [Appendix 2]
In the example the circle seems to
touch AC. In general this is not the case. Figure 6 presents another example.
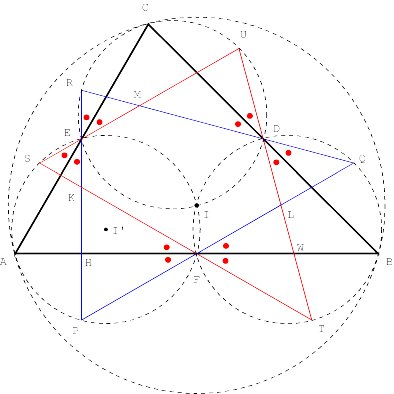
This time the hexagon AC"BA"CB" is not convex.
If j
becomes a right angle, the hexagon and circle are reduced to only one point,
the orthocentre.
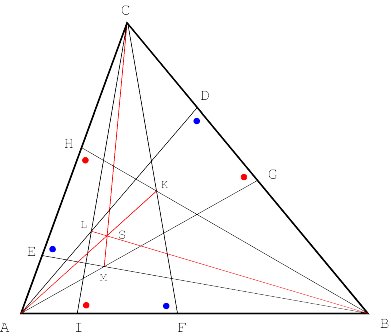
More properties of oblique altitudes Let K, L and M be the following points of intersection of the j -altitudes: K = BH ÇCF, L = AD ÇCI and M = AG ÇBE. It may be proven that the straight lines AK, BL and CM are concurrent (Figure 7) [for a proof see Appendix 3].
Similarly, it may be proven that the straight lines AP, BQ, and CR are concurrent, being P = BE ÇCI, Q = AG ÇCF and R = AD ÇBH (Figure 8).
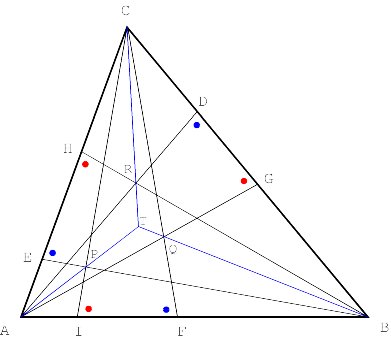
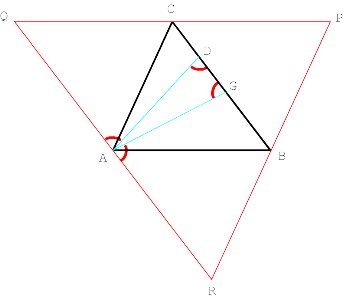
Introducing oblique bisectors Consider any triangle ABC. The line that passes through the midpoint of a side and that is perpendicular to the side is called a perpendicular bisector (or mediator). According to a classical theorem of plane geometry the three perpendicular bisectors of ABC are concurrent. The common point of the three perpendicular bisectors is called the circumcentre of the triangle. Now let us consider any angle j . We will call a bisector a j -bisector if it forms an angle equal to j with the line segment (Figure 9).
Properties of oblique bisectors Consider any triangle ABC. Let f be an angle different in size from a , b and g . Let D, E and F be the midpoints of the sides of ABC. The three right j -bisectors form triangle PQR, whereas the three left j -bisectors generate triangle STU (Figure 10). Easily it may be seen that these triangles are similar to ABC.
Moreover, the points A, E, F, P, S, and the circumcentre I lie on a circle. Its centre is I, the midpoint of AI (Figure 11).
Similarly, the points F, T, B, Q, D, and I lie on a circle, just like the points D, U, C, R, E and I on another circle. The diameter of the circles is equal to the radius of the circumcircle of triangle ABC (Figure 12).
The six points P, T, Q, U, R, and S lie on a circle that has the cirrcumcentre I as its centre (Figure 13). The quadrilaterals ABTP, BCUQ and CASR are isosceles trapezoids.
More properties of oblique bisectors The lines DK, EL and MK are concurrent (Figure 14). When j turns 0, we have the particular case of the concurrence of the three medians.
We may also consider the other pairs of corresponding oblique j -bisectors. If U = EM ÇFL, V = DM ÇFK and W = DL ÇEK, then the lines DU, EV and FW are concurrent (Figure 15).
Oblique altitudes and oblique bisectors Let PQR be the triangle circumscribed to triangle ABC such that PQ // BA, QR // CB, and RP // AC. The perpendicular bisectors of PQR are the altitudes of ABC. Similarly the j -bisectors of PQR are the j -altitudes of ABC (Figure 16). This explains the similarity between the properties of the j -bisectors and those of the j -altitudes.
As CDB and CFB are similar triangles, we have CB : CB = CD : CF, or (1) CB· CF = CD · CB. The points A, B D and H lie on a circle. Therefore, we have (2) CD · CB = CH · CA. As CA"H and CAI are similar triangles, we have (3) CH · CA = CA" · CI. Taking into account (1), (2) and (3), we find CB· CF = CD · CB = CH· CA = CA" · CI. By consequence, A"B // AB and as CF = CI, it follows that (4) CB = CA". In the same way, we find B"C // BC, AB" = AC, AC" // AC and BA = BC". As the triangles ABF and ACI are similar, we have, on the one hand (5) AF · CI = AI · BF. We have on the other hand (6) AI · BF = B"I · CF, as the triangles B"AI and BCF are similar too. Comparing (5) and (6), we find AF·CI = AI · BF = B"I·CF. By consequence, B"A // AB and, taking into account CI = CF, we find (7) AF = B"I. In the same way, one may show that C"B // BC, C"G = BD, A"C // CA and A"H = CE. Taking into account (4), (7) and CF = CI, we find that AB = A"B". Similarly, we may conclude BC = B"C" and AC = A"C". Therefore, the triangles ABC and A"B"C" are congruent. Let O be the orthocentre of triangle ABC. The altitude relative to the side B"A of the isosceles triangle B"CA passes through the orthocentre. By consequence, we have OB" = OA. In the same way, we find OA" = OB, OA" = OC, OC" = OA, OC" = OB and OB" = OC. Therefore OA = OC" = OB = OA" = OC = OB". In other words, the vertices of the hexagon AC"BA"CB" lie on a circle of which the centre coincides with the orthocentre of ABC. Let S = AK ÇBL. We will verify if CM passes through S. We may introduce rectangular Cartesian coordinates such that A º (0, 0), B º (1, 0) and C º (p, q). (a) The equations of BH and CF are given by: (BH) y = tg(a +j ) (x1), (CF) y q = - tg(j ) (xp). Being K = BH ÇCF, we find: xK = [q + tg(a +j ) + p tg(j )] / [tg(j ) + tg(a +j )] yK = [tg(a +j ) (q + (p 1) tg(j ))] / [tg(j ) + tg(a +j )] By consequence, the equation of AK is given by: (AK) y = (yK / xK) x = ([tg(a +j ) (q + (p 1) tg(j ))] / [q + tg(a +j ) + p tg(j )]) x Taking into account tg(a +j ) = [tg(a ) + tg(j )] / [1tg(a ) tg(j )] and tg(j ) = q / p, the expression for the gradient of AK may be written as: k = mAK = [q + (p 1) tg(j )] / [p+1 q tg(j )], or, k = [q + (p-1)f] / [p + 1 qf], where f = tg(j ). (b) The equations of AD and CI are given by: (AD) y = - tg(b +j ) x, (CI) y q = tg(j ) (xp). Being L = AD ÇCI, we find: xL = [ - q + p tg(j )] / [tg(j ) + tg(b +j )] yL = [- tg(b +j ) (- q + p tg(j )] / [tg(j ) + tg(b +j )] By consequence, the equation of BL is given by: y = (yL / (xL 1)) x = ([- tg(b +j ) (- q + p tg(j ))] / [- q tg(b +j ) + (p 1) tg(j )]) (x 1) Taking into account tg(b ) = q / (1 p), the gradient of BL may be expressed as: d = mBL = [ - q + p tg(j )] / [p2 + q tg(j )] = (c) Being the equations of AK and BL given by (AK) y = kx, (BL) y = d (x 1), the coordinates of their point of intersection S are given by: xS = d / (d-k) and yS = dk / (d-k). (d) The equations of the straight lines AG and BE are given by: (AG) y = - tg(bj) x (BE) y = tg(aj) (x 1) Being M = AG ÇBE, we find: xM = tg(aj) / [tg(aj) + tg(bj)] yM = [-tg(aj) tg(bj)] / [tg(aj) + tg(bj)] and the equation of CM becomes: y q = (x p). CM passes through S if and only if (1) (yM q) / (xM -p) = (yS q) / (xS -p) (e) Taking into account tg(bj) = [tg(b ) tg(j )] / [1 + tg(b ) tg(j )] = [q (1-p)f] / [(1-p) +qf] and tg(aj) = [tg(a ) tg(j )] / [1 + tg(a ) tg(j )] = [q - pf] / [p + qf]. the left member of equation (1) may be transformed and simplified in the following manner: = [ - tg(aj) tg(bj) q (tg(aj) + tg(bj))] / [(1 p) (tg(aj) p tg(bj)] = [-2q2 + (q2q3 2p2q +2pq) f + (-p+p2 +q2) f2] / [(1 2p) (q + (-p+p2 + q2)f] = [(f 2q) (q + (-p+p2 +q2) f ) ] / [(1 2p) (q + (-p+p2 +q2) f ) ] = (f) The right member of equation (1) may be transformed and simplified in the following manner: (yM q) / (xM -p) = = [dk q (d k) ] / [(1 p) d + pk ]= = [-2q2 + (q+2q3 +2p2q 2pq) f + (p p2 q2) f2] / [(1 2p) (q + (p p2 q2)f]= = [(f 2q) (q + (p p2 q2) f ) ] / [(1 2p) (q + (p p2 q2) f ) ]= = [-2q + f] / [1 2p]. (g) We arrive at (yM q) / (xM -p) = [-2q + f] / [1 2p] = (yS q) / (xS -p). In other words, CM passes through S. The lines AK, BL and CM are concurrent. Q.E.D.
|