|
Permutations and Copi mats, Chidenguele, Mozambique
Paulus Gerdes Centre for Mozambican Studies and Ethnoscience Universidade Pedagógica Maputo, Mozambique
Near the shores of the Indian Ocean, about 270 km northeast of Maputo, the capital of Mozambique in Southeast Africa, lies the village of Chidenguele (District of Manjacaze, Gaza Province). From the top of the hill, where a church is built – Chidenguele means ‘the highest point’ in the local, Copi language – one can see far around. The Copi (or Chope) culture is famous for its ‘timbila’ xylophone music. In June 1977, I visited Chidenguele for the first time for the celebrations of the second anniversary of Independence Day of the country. In 1999, I visited Chidenguele on an ethnomathematical fieldtrip together with my colleague Marcos Cherinda and I had the opportunity to speak with Mr. Simbine, a local hat weaver.
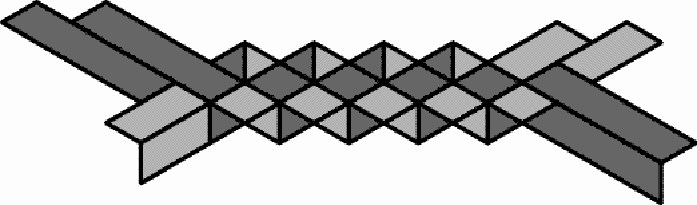
The author acquiring several hats from Mr. Simbine (Photograph taken by Marcos Cherinda) Mr. Simbine makes the hats by knitting together successive circuits of a spiral. The spiral consists of a hexagonally woven zigzag band:
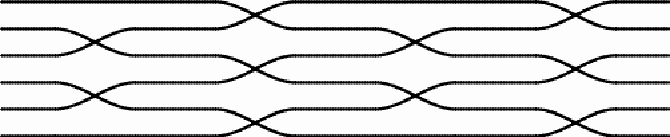
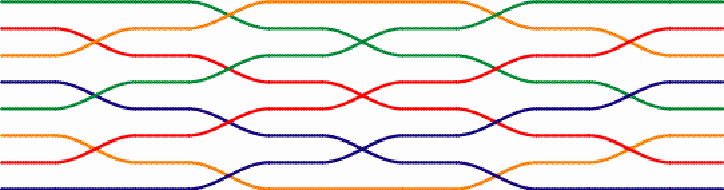
Hexagonally woven zigzag band These woven bands may be explored in several attractive ways in mathematics education (cf. Paulus Gerdes, Geometry from Africa, The Mathematical Association of America, Washington DC, 1999, pp. 110-112). During the last few years I have been visiting Chidenguele more regularly for (short) holidays, staying with my family at the Paraíso (Paradise) lodge in the dunes near the beach (www.chidbeachresort.com).
My daughter Likilisa and her friend Marla playing in Paradise In December 2009, during one of our stays in Paradise, I became intrigued with the ceilings of our room. To keep the rooms cool, the ceilings are made from simple traditional mats made in the area. The mats normally consist of reeds of equal length that are bound together by pairs of threads that are simultaneously interlaced up and down in such a way that when one thread goes over the reed, the other passes under it. Looking at a finished mat the threads run perpendicular to the reeds.
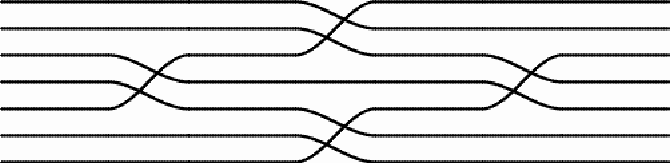
Most ceilings of the rooms at Paradise are made of these simple rectangular reed mats with a design of parallel thread lines. However, I noticed that the artisan(s) who had made the mats hung onto the ceiling in two rooms, had deliberately changed the directions of the threads in the middle of the mats, producing different designs, as the following example illustrates.
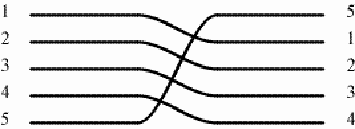
Changing directions of the five threads in the middle of the mat After changing the direction twice, each pair of threads continues the (horizontal) line followed before the changing by another pair of threads. In other words, the mat weaver permuted the (horizontal) thread lines. In the case of this mat we have two sets of switches:
At the first set of switches,
the first thread line becomes the second; the second becomes the third; the third becomes the fourth; the fourth becomes the fifth, and the fifth becomes the first. In other words, we are dealing with a permutation of the order of the lines, and this permutation can be noted in the cycle notation as follows: (1 2 3 4 5). At the second set of switches,
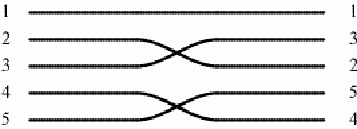
the first thread line continues the first, but the second interchanges with the third, and the fourth interchanges with the fifth. Once again, we are dealing with a permutation of the order of the lines, and it can be noted as: (2 3) (4 5). Whereas the first set of switches displays a rotational symmetry, the second set has axial symmetry. Jointly the two sets of switches of direction on the mat create a product of permutations: (1 2 3 4 5) x (2 3) (4 5) = (1 3 5). At the end, after switching twice, the second thread line returns to itself, just like the fourth:
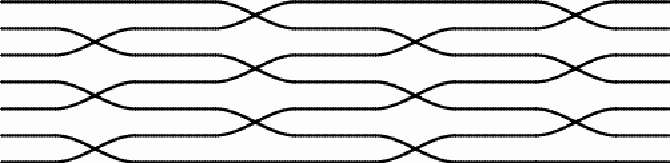
On one other mat hanging on the ceiling of one of the rooms at Paradise, the switches of the direction involve five central thread lines too. The central part of this mat has the following design:
The first and third sets of switches have two axes of symmetry. They interchange the second with the fourth thread line, and the third and the fifth thread line too. The respective permutation may be denoted as (2 4) (3 5). The second sets of switches can be denoted as (1 2 3) (4 5). Jointly, the effect of the three sets of switches of the thread lines is the product of the three permutations: (2 4) (3 5) x (1 2 3) (4 5) x (2 4) (3 5) = (1 4 5) (2 3).
Detail of the mat: The first set of switches
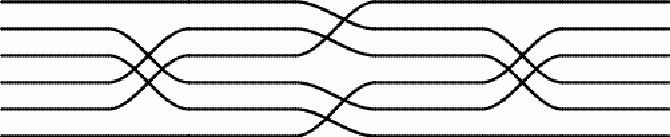
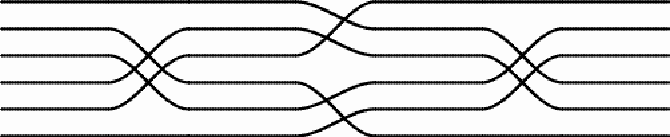
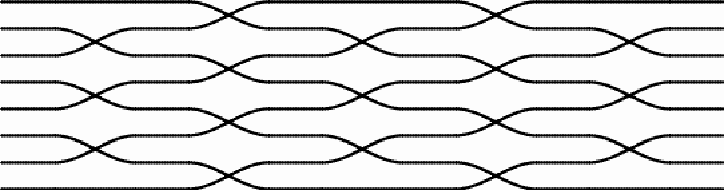
On the ceilings of the rooms at Paradise, there are ten mats with two or more sets of switches of direction. On five of the mats the switches involve six central thread lines: (1)
The design presents a rotational symmetry. The first and third sets of switches are the same, and have two axes of symmetry. The second set of switches displays rotational symmetry. The first and third permutations can be noted as (2 4) (3 5), and the second permutation as (1 2 3) (4 5 6). Together, the effect of the three sets of switches of the thread lines is the product of three permutations: (2 4) (3 5) x (1 2 3) (4 5 6) x (2 4) (3 5) = (1 4 5) (2 3 6), where the first thread line becomes the fourth, the fourth becomes the fifth, and the fifth becomes the first, etc.
Detail of the mat: second set of switches (2)
The design is similar to the previous design, however the lower switch of the second set of switches has been reflected in the horizontal axis. As a consequence the design displays a mirror-symmetry. This time, the permutation that results from the second set of switches can be denoted as (1 2 3) (4 6 5). The effect of the three sets of switches of the thread lines is the product of three permutations: (2 4) (3 5) x (1 2 3) (4 6 5) x (2 4) (3 5) = (1 4 5) (2 6 3).
Detail of the mat: second and third set of switches (3)
Each of the sets of switches of thread lines displays a double symmetry, but the design as a whole does not have symmetry. The symmetry is broken by the third set of switches. The second permutation can be denoted as (1 2) (3 4) (5 6) and the third as (3 5) (4 6). The product of the three permutations is (2 4) (3 5) x (1 2) (3 4) (5 6) x (3 5) (4 6) = (1 2 5 6 3 4). (4)
The first set of switches is equal to the third set. The corresponding permutation may be denoted by (1 4 2 5 3). The second permutation is equal to the second one in the previous case. The product of the three permutations results in: (1 4 2 5 3) x (1 2) (3 4) (5 6) x (1 4 2 5 3) = (2 6 3 5), where the first and the fourth thread line return to themselves:
Detail of the mat: First and second set of switches
(5)
The design of this mat displays an axial symmetry. This time there are four sets of switches of the thread lines. The mat maker opted for sets of switches with double symmetry. The first set is equal to the third set, and the corresponding permutation may be denoted by (2 3) (4 5). The second set is equal to the fourth set of switches and may be denoted by (1 2) (3 4) (5 6). The cumulative effect of the four sets of switches is the product of the four permutations: (2 3) (4 5) x (1 2) (3 4) (5 6) x (2 3) (4 5) x (1 2) (3 4) (5 6) = = (1 2 4 6 5 3) x (1 2 4 6 5 3) = (1 4 5) (2 6 3)
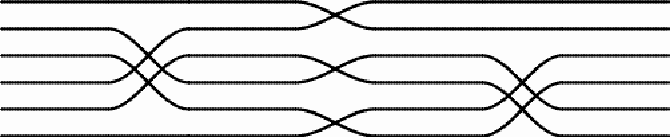
Detail of the mat: First and second sets of switches On two mats at Paradise, the sets of switches involve seven central thread lines. In the first case, there are three sets of switches:
Detail of the mat: Second and third set of switches The four switch elements are all equal: Both the switch elements as the design itself display rotational symmetry. The first and third sets of switches are characterized by the permutation (3 4 5). The second set corresponds to the permutation (1 2 3) (5 6 7). The three sets together generate the following product of permutations: (3 4 5) x (1 2 3)(5 6 7) x (3 4 5) = = (1 2 4 6 7 3 5).
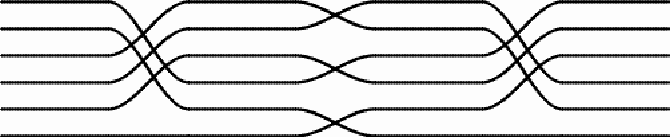
In the second case, there are four sets of switches:
This design presents rotational symmetry. All switch elements are interchanges of two thread lines and have double symmetry:
The first and third sets of switches lead to the permutation denoted by (2 3) (4 5) (6 7), whereas the second and fourth sets correspond to the permutation (1 2) (3 4) (5 6). The four sets together produce the permutation: (2 3) (4 5) (6 7) x (1 2) (3 4) (5 6) x (2 3) (4 5) (6 7) x (1 2) (3 4) (5 6) = = (1 4 7 3 2 6 5). The five sets of switches of the tenth ceiling mat in Paradise involve eight central thread lines:
The design displays both rotational and axial symmetry. The first, third and fifth sets of switches are equal and correspond to the permutation denoted by (2 3) (4 5) (6 7). The second and four sets of switches are equal too. The permutation involved may be denoted by (1 2) (3 4) (5 6) (7 8). The cumulative effect of the five sets of switches is the product of the five permutations: (2 3) (4 5) (6 7) x (1 2) (3 4) (5 6) (7 8) x (2 3) (4 5) (6 7) x x (1 2) (3 4) (5 6) (7 8) x (2 3) (4 5) (6 7) = = (1 5) (2 7) (4 8). In other words, the third and sixth thread line return to themselves, whereas the first and fifth are interchanged, just like the second and the seventh, and the fourth and the eighth. The double symmetry of the design reflects itself in the product permutation:
In all ten mats, the sets of switches are built up of symmetrical elements, either with only rotational symmetry
or with double symmetry:
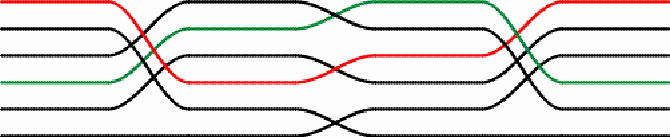
It is clear that symmetry is important for the artisan(s) who made these mats used at the ceilings of the rooms at Paradise. Sometimes, however, the cumulative effect of the permutations may be more important than symmetry, as a mat I acquired, in 1999, along the road in the neighboring district of Zavala (Inhambane Province), illustrates.
The design has a horizontal axis of symmetry:
The design easily could also have had a vertical axis of symmetry, but the artisan did not want it that way. Let us follow the six thread lines:
The mat maker wished that each thread line ultimately would return to itself. Symmetry had to be broken. Conclusion The example of the mats hung unto the ceilings of some of the rooms at the Paradise resort in Chidenguele show that some Copi artisans have been challenged by the material when making their traditional sleeping or floor mats. They have been experimenting with symmetrical switch elements of the threads, inventing both symmetrical and non-symmetrical designs, and producing various permutations. These designs may very possibly go unnoticed by the visitors to the resort, and surely the mat makers were not financially awarded for their creativity and innovation. The artisans may be relatively poor materially, and with little or no formal schooling, but they display their artistic and intellectual potential, endeavor and richness in the mats they weave. One way to value the creativity of these mat makers is to explore their ideas in studying permutations at various levels of mathematics education, including mathematics teacher education in Mozambique. Another way to celebrate the ingenuity and imagination of the artisans is to present their work internationally in the on-line journal Visual Mathematics, a paradise on the web.
|