|
A way to interlace an octagonal prism invented by a Copi basket maker in Southeast Mozambique
Paulus Gerdes Centre for Mozambican Studies and Ethnoscience Universidade Pedagógica Maputo, Mozambique
Basket weavers in various parts of Southern Africa interlace buttons and handles in the shape of square prisms. The following photograph displays a basket I acquired, in 1977, in Ponta de Ouro in the extreme South of Mozambique. The basket has both a square-prism-shaped handle and two square-prism-shaped buttons.
Detail of the basket: A button with the shape of a square prism Square-prism-shaped handles are common on Zulu baskets from the East of South Africa, as the following two examples in my collection illustrate:
Lid of a Zulu basket acquired in 2002: square-prism-shaped handle At the end of July 2002, I saw, for the first time, a basket with a button with a distinctly different prism shape. On the streets of Maputo, the capital of Mozambique, a young man was selling two sets of similar handbags: one with the usual square-prism-shaped button and the other with a more rounded-off, circular type of button:
Handbag with ‘rounded off’ button
Close-up of the button The seller told me that his uncle, a Copi speaking basket weaver from the South of the Inhambane province, had made the handbags. The shape of the button invented by the basket weaver is that of an octagonal prism:
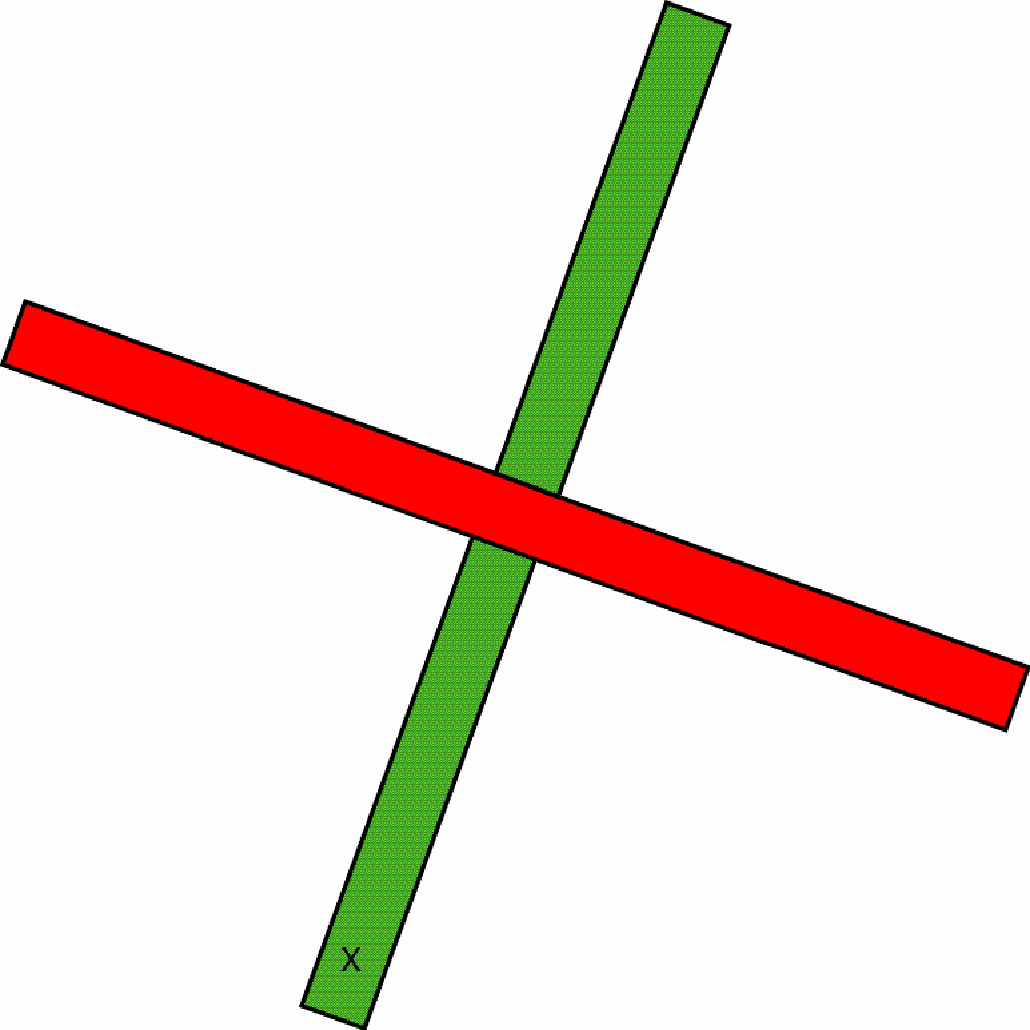
Several close-ups of another ‘rounded-off’ button Wherein does the invention of the Copi basket weaver lie? Let us see, first of all, how a normal square-prism-shaped button can be made. One starts with two strips of the same width and length:
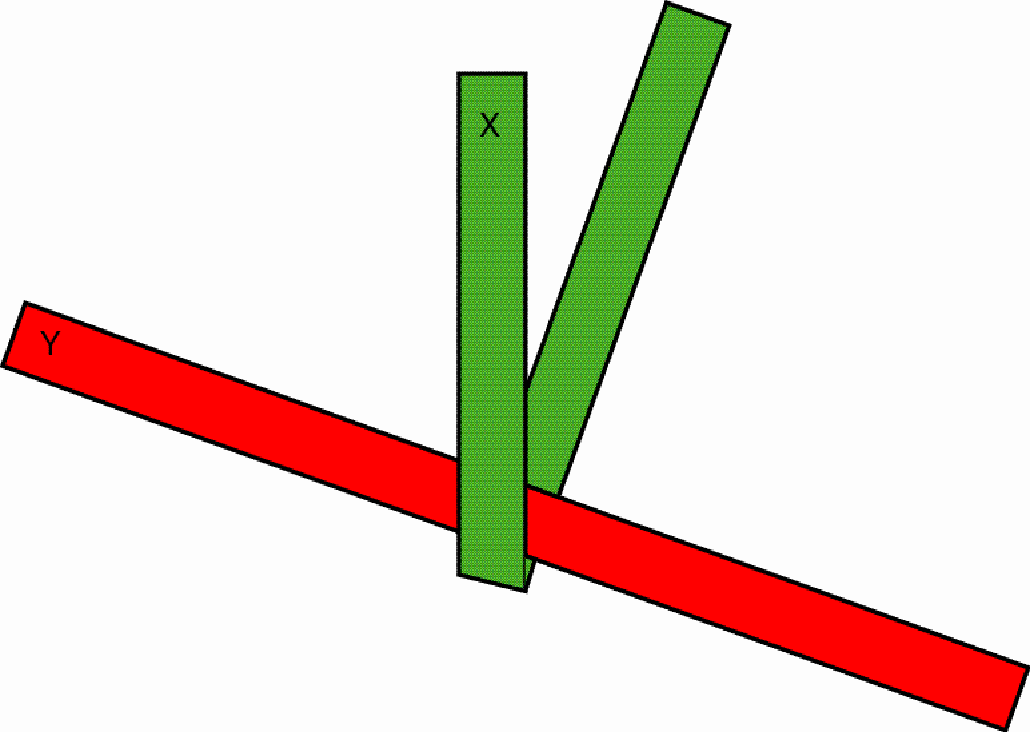
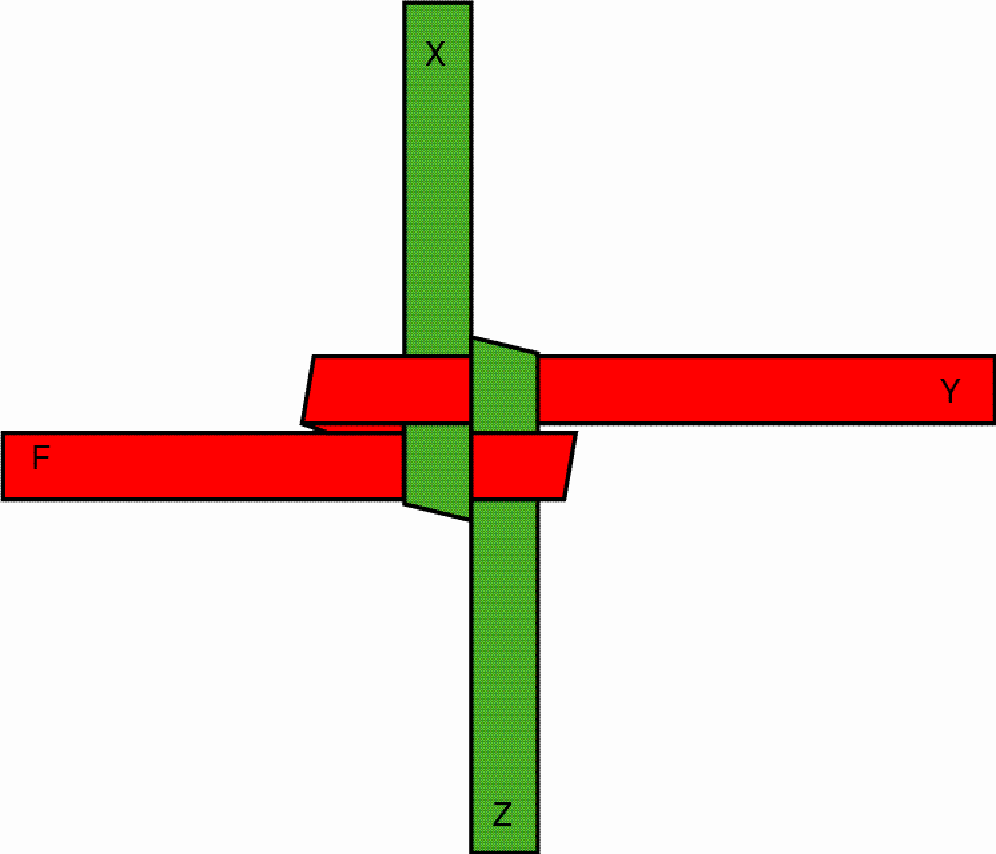
One interlaces the two strips
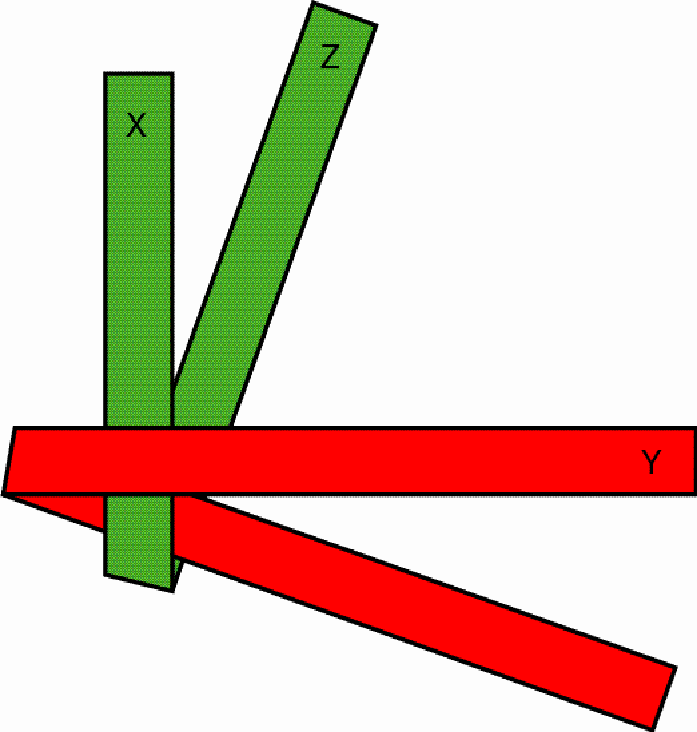
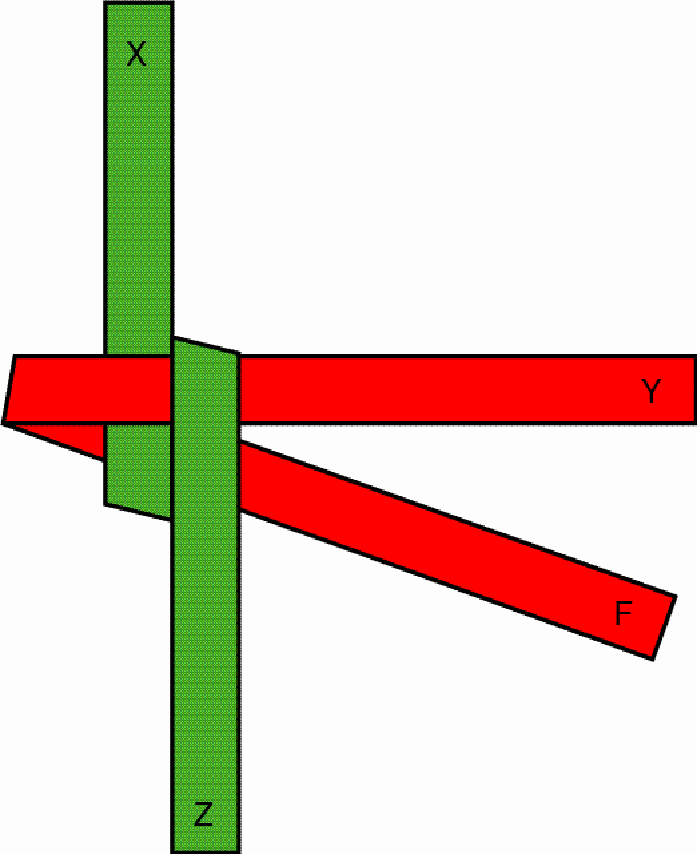
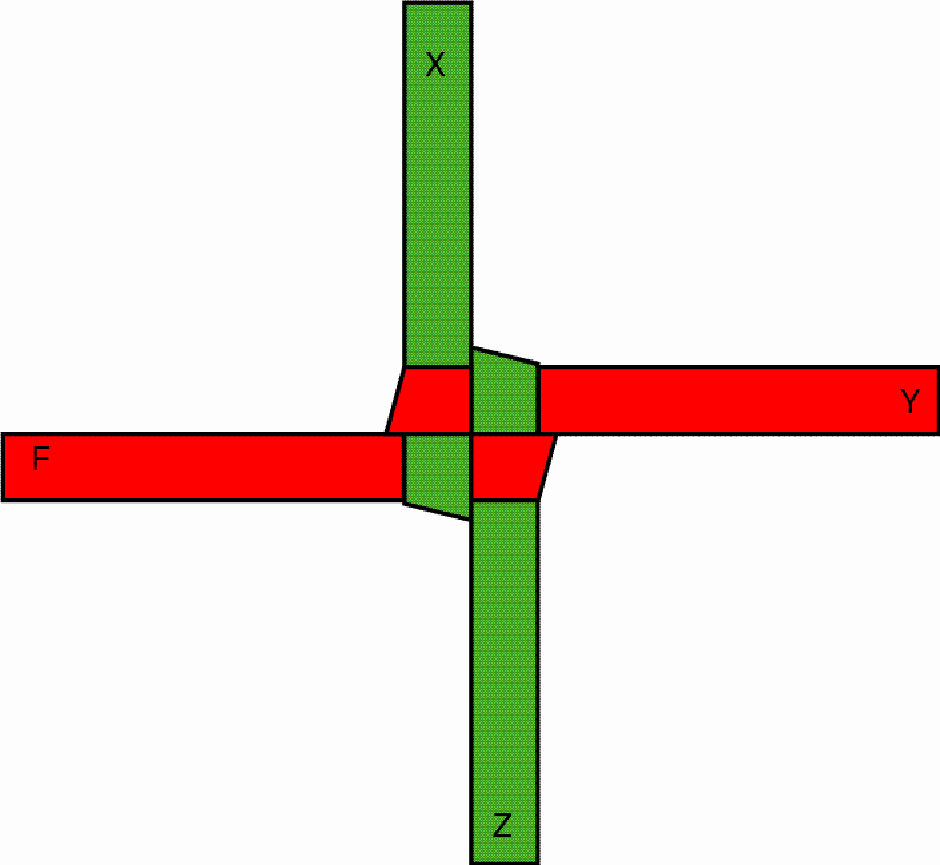
One pulls the outstanding red part (F) over the first protruding green part (Z) and under the second green part (X), so that, after drawing tighter, a stable knot emerges:
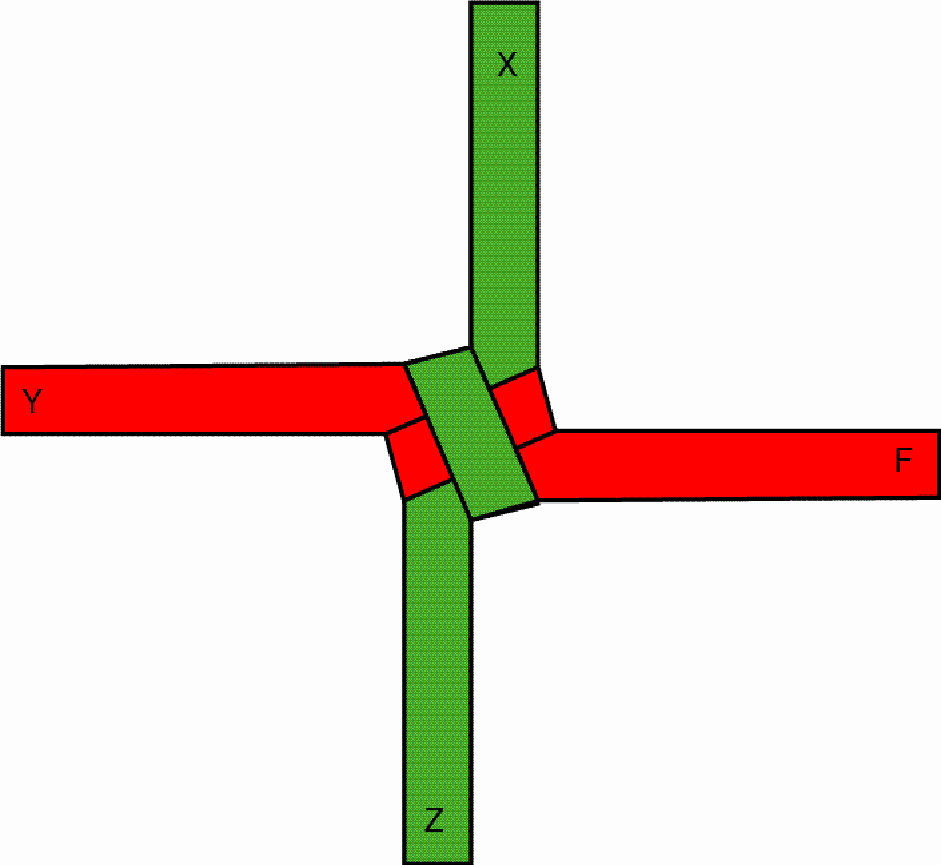
This knot constitutes the first layer of the square-prism-shaped button. By folding and interweaving the protruding parts of the strips once more the second layer is built up, etc. The other face of the stable knot looks like the following, as may be seen on the first basket: The octagonal-prism-shaped button may be interlaced / plaited basically in the same way as the square-prism-shaped button. The only difference lies in the fact that, from one layer to the next, the artisan changes the direction of the strip parts by 45 degrees. The change of direction results from folding each protruding strip part in such a way that its outer edge passes, after the folding, through the centre of the square so that it becomes an inner edge at this stage:
Let us follow the first steps of the interlacing process. To make it clearly visible, the basic knot consists of cardboard strips of four colours:
Now the red strip changes direction by 45 degrees:
The blue strip is folded in the same way:
The green strip is folded similarly, going over the red and under the blue strip:
To conclude the first layer of the octagonal-prism-shaped button, one folds the yellow strip, and pulls it over the blue and under the red strip:
After interlacing a few more layers, our octagonal-prism-shaped button made out of four cardboard strips looks like:
The octagonal base of the button invented by the Copi basket weaver is a regular octagon, as can be proven in many ways. Various attractive forms to explore and incorporate this Copi invention and innovation into mathematics (teacher) education may be conceived. One interesting question to ask the students is how to prove that the constructed octagon is a regular octagon (cf. the booklet: Paulus Gerdes, Prazer na Geometria: Um belo botão do Sul de Moçambique [Pleasure in Geometry: A beautiful button from the South of Mozambique], Maputo, 2002). From 2003 until today, I have not seen any more handbags with the octagonal-prism-shaped button. The usual square-prism-shaped button continues to be used every day.
Maputo, February 2010 |