|
in proportional parts Paulus
Gerdes
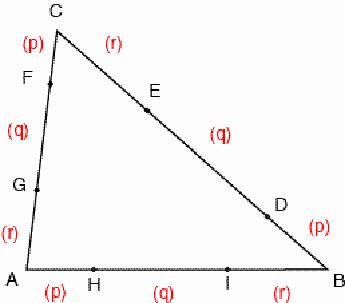
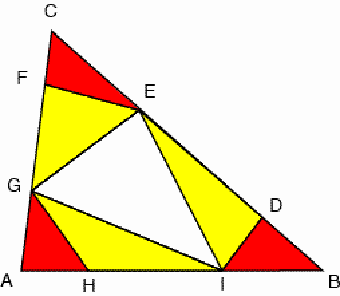
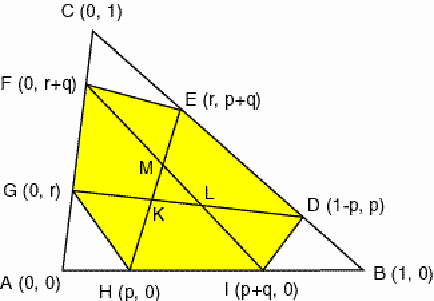
Figure 1 Consider an arbitrary triangle ABC. Let D and E be points on the side BC, F and G points on CA and H and I points on AB, such that BD : DE : EC = CF : FG : GA = AH : HI : IB = p : q : r with p+q+r=1, being p, q and r positive numbers (Figure 1). The areas of the corner triangles AHG, BDI and CFE are equal to pr times that of ABC. The areas of the triangles FGH, HID and DEF are equal to pq times that of ABC. Furthermore, the areas of the triangles GHI, IDE and EFG are equal to qr times that of ABC. In Figure 2 the triangles that have equal areas are represented by the same colour.
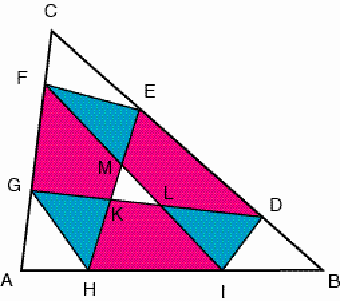
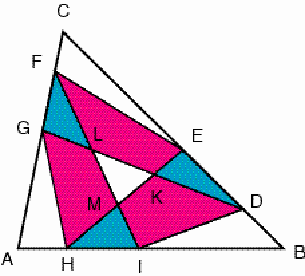
Figure 2 Let K, L, and M be the intersection points of the diagonals DG and EH, FI and DG, and EH and FI. What may be said about the areas of the triangles and quadrilaterals in which the diagonals DG, EH, and FI dissect the hexagon DEFGHI? (Figure 3) 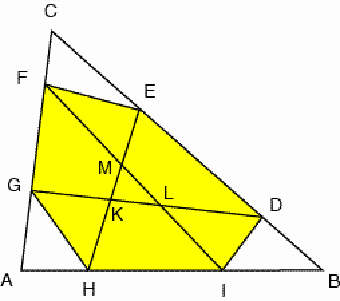
Figure 3 We will prove the following: (1) The areas of the quadrilaterals DEFG, FGHI, and HIDE are equal to q times that of ABC; (2) The areas of the triangles GHK, IDL and EFM are equal to (p2 – 2pr + r) (r2 – 2rp + p) / (p2 + r2 – pr + q) times that of ABC; (3) The areas of the triangles DEK, FGL and HIM are equal to q2 (1 – p) (1 – r) / (p2 + r2 – pr + q) times that of ABC; (4) The area of the triangle KLM is equal to (3pr – 2p – 2r + 1) 2 / (p2 + r2 – pr + q) times that of ABC. The expressions (2),
(3), and (4) are symmetrical relative p and r. In Figure
4 the triangles and quadrilaterals that have equal areas are represented
by the same colour.
Two types of situations Figure 4 The area of DEFG is the difference of the areas of the triangles DCG and ECF. By consequence, the area of DEFG is equal to (q+r)(p+q) – pr = pq +q2 + qr = q times the area of ABC. The same holds for the quadrilaterals FGHI and HIDE. We may introduce Cartesian
coordinates in such a way that A º
(0 , 0), B º
(1 , 0) and C º
(0 , 1). Consequently, we have D º
(1-p , p), E º
(r , p+q), F º(0
, r+q), G º
(0 , r), H º
(p , 0), and I º
(p+q , 0) (Figure 5).
Figure 5 The equations of the straight lines DG, EH and FI are given by: EH: y = (x – p) or x = p if p = r ; FI: y = – (x – p – q). xL = yM = q (1 – p) (1 – r) / (p2 + r2 – pr + q) xM = yK = (1 – r) (p2– 2pr + r) / (p2 + r2 – pr + q).
i.e. by xK (p2 – 2pr + r) / (1 – p) = (p2 – 2pr + r) (r2 – 2rp + p) / (p2 + r2 – pr + q). A similar calculation leads to the same result for the triangles IDL and EFM. On the one hand, the
ratio of the areas of the triangles FGL and ABC is equal
to q.xL and, on the hand, the ratio of the areas
of the triangles HIM and ABC is equal to q.yM.
By consequence, both ratios are equal to q2 (1 – p)
(1 – r) / (p2 + r2 – pr
+ q). The ratio of the areas of the triangles DEK and ABC
is given by the absolute value of the determinant
i.e. by - qxK – q yK + q = q2 (1 – p) (1 – r) / (p2 + r2 – pr + q). The ratio of the areas of the triangles KLM and ABC is equal to the absolute value of the determinant
i.e. by [(1–p)2 (r2–2rp+p) 2 + (1–r)2 (p2–2pr+r)2 + q2 (1–p)2 (1–r)2 – (1–p)(1–r) (p2–2pr+r) (r2–2rp+p) – q(1–p)2 (1–r) (r2–2rp+p) – q(1–p)(1–r)2 (p2–2pr+r)] / (p2 + r2 – pr +q)2 or (9p2r2 – 12p2r – 12pr2 + 4p2 + 4r2 + 14pr – 4p – 4r + 1) / (p2 + r2 – pr + q) = (3pr – 2p – 2r + 1) 2 / (p2 + r2 – pr + q) The last expression
shows that the diagonals DG, EH and FI are concurrent
if and only if 3pr – 2p – 2r + 1 = 0 or p =
(2r-1)/(3r-2) and r = (2p-1)/(3p-2).
Figure
6 displays the example p =1/4 and
r =2/5 .
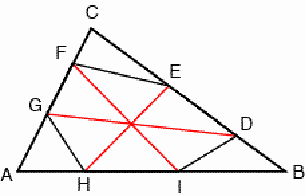
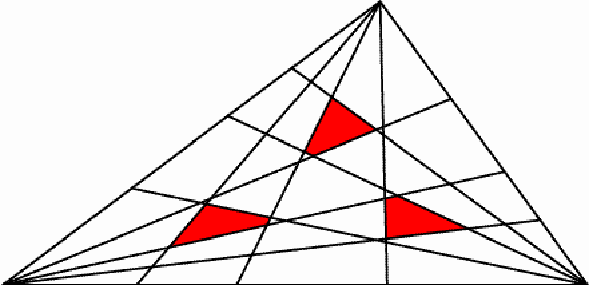
Figure 6 In general, the centroids of the triangles ABC and KLM coincide. In the particular situation that the hexagonal diagonals DG, EH and FI are concurrent, their common point is the centroid of the triangle ABC. Let us now consider the Cevians AD, AE, BF, BG, CH and CI. They dissect the triangle ABC in various triangles and quadrilaterals. Figure 7 displays an example. 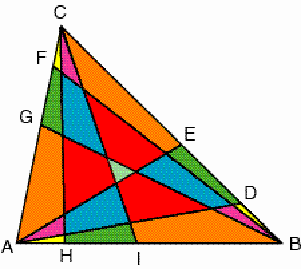
Figure 7 It may be shown that
these Cevians dissect the triangle ABC into sets of triangles, quadrilaterals
and possibly other polygons, and a central triangle or a central hexagon;
each set contains three elements of equal area.
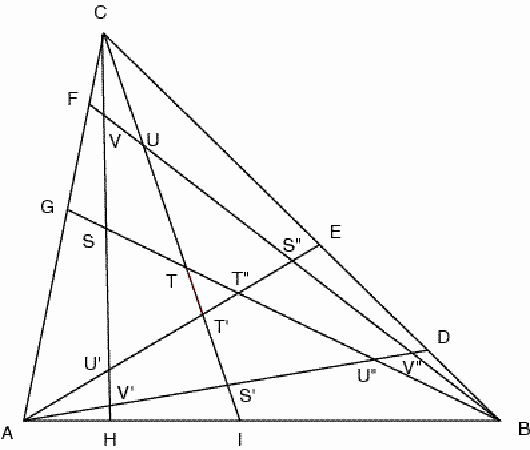
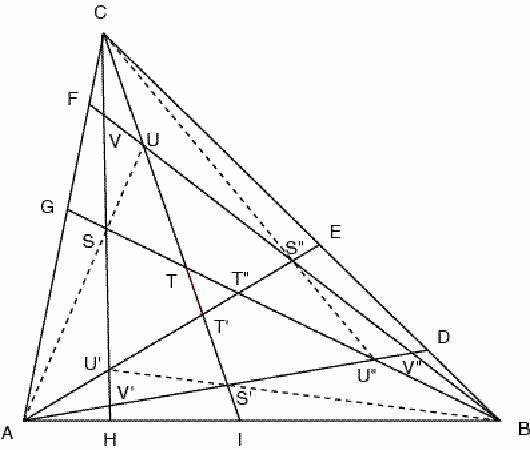
Figure 8 Let S and T
be the points of intersection of BG with CH and CI;
let V and U be the intersection points of BF with
CH and CI (Figure 8). We may use a coordinate
system such that A º
(0, 0), B º
(1, 0), and C º
(0, 1). By consequence, we have H º
(p, 0), I º
(p+q, 0), G º
(0, r), and F º
(0, q+r). The coordinates of S, T, U
and V are given by:
Figure 9 The proportion of the area of the quadrilateral AHSG to the area of the triangle ABC may be calculated. It is given by pr(2-p-r)/(1-pr). If one selects the Cartesian coordinate system with B º (0, 0), C º (0, 1) and A º (1, 0), one finds similarly that the proportion of the area of quadrilateral BDS’I to the area of the triangle BCA is also pr(2-p-r)/(1-pr). Continuing in a cyclic order and selecting the coordinate system with C º (0, 0), A º (0, 1) and B º (1, 0), one finds that the proportion of the area of quadrilateral CFS"E to the area of the triangle CAB is once more pr(2-p-r)/(1-pr). The same reasoning may be applied to other polygons in which the Cevians dissect the triangle ABC. We may conclude that polygons that correspond in cyclic order have equal area. This result may be easily generalised: If the sides of a triangle ABC are divided in the proportion p1 : p2 : …. : pn, where p1, p2, …, p(n-1), and pn are positive numbers satisfying p1 + p2 + …. + pn = 1, then the triangle ABC is dissected in sets of corresponding polygons and possibly a central polygon; each set contains three elements of equal area. Figure
10 presents an example where n=4. A set of three quadrilaterals
with equal area is marked.
Figure 10 If additionally, p1 = pn , p2 = pn-1 , p3 = pn-2 , …, then each set contains six elements of equal area. Figure
11 presents an example where n=4, and p1 =
p2 = p3 = p4 =1/4.
The central polygon is reduced to a point.
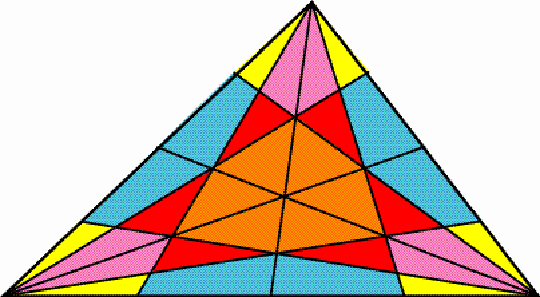
Figure 11
|