Estimating mathematical information on Graphs: A Scientific Approach
Raghu R. Gompa, Ph. D.
Professor of Mathematics
Department of Mathematics
School of Science and Technology
P.O. Box 17610
Jackson State University
Vijaya L. Gompa, Ph. D.
Associate Professor of Mathematics Education
Director of Master of Science in Teaching Programs
Department of Mathematics
P.O. Box 17610
Jackson State University
Jackson , Mississippi 39217
1 Introduction
In first calculus classes (see, for example, [ 1]),
there are many activities which involve graphs. When available, individuals
can look at the information provided as to how the graphs were prepared
and use this information to determine certain important points that lie
on the graphs. A problem arises when graphs are presented without any numbers
as to how they were made. In situations such as this, the only way to determine
the rates of change and the points that provide crucial information (such
as those on tangent lines to find instantaneous rate of change) is by estimating.
Students must figure out a way to accurately determine these points if
the exercises in the text are to be effective and worthwhile practice.
This is not a challenge just for calculus students. Recent books on elementary
or intermediate algebra (see, for example, [ 2]) present
problems of reading graphs accurately. The size of the graph is critical to the type of tool
that is used to estimate the points. Conventional items such as rulers
are often very ineffective on very small graphs typically provided in textbooks.
The focus here will be on determining the best method
of estimating on small graphs that are marked only incrementally, as graphs
encountered by students in a calculus class or even in algebra class. Several
methods are discussed, including the use of a tool that the authors have
found to be most effective in teaching first year calculus class.
The simplest estimating plan is just to look at the
graph and "eyeball" the estimated distance between the points. This may
work on graphs where the answer is obvious or falls on a marked line, but
for most purposes this will not be an effective measuring plan.
Another plan is similar to that taught in elementary
school to estimate map distances. One takes a plain piece of paper and
mark the distances on that paper and then measures the marked section against
a scale given at some other place on the page. This works if the section
that needs to be measured on the graph can be compared accurately to a
scale somewhere else on the graph. If this section is longer or shorter
than the scale one runs into difficulties in determining the differences.
Also, one sometimes loses measurement accuracy by transferring measurements
so many times.
A ruler may be a good estimating tool for students working
with graphs. The ruler provides a nice straight edge which the students
can trace against. It allows measurements that will assist students in
measuring more accurately the distance between points on the graph so that
they can determine the coordinates of a specific point. One problem with
the ruler is that it can be thick and difficult to work with on very small
graphs.
Another option that students may try is a transparent
ruler. It is easier to use because students can see through to the paper
so they know exactly what they are marking and can see their graph under
the ruler while they are drawing their lines. While this is a good instrument
for estimating, there is still the problem that the ruler has only one
side and in graphing one often needs to measure two coordinates. With a
ruler, one has to measure the x-coordinate and then turn the ruler around
and measure the y-coordinate. One may also measure inaccurately if the
ruler is not positioned properly. These types of rulers can also be quite
thick and difficult to work with on small graphs.
In order to be a little more accurate, students may
attempt to use graph paper. While graph paper with large squares is not
much better than plain paper, it does provide a good scale if the student
is working with a large graph. The incremental markings are quite helpful.
However, when working with small graphs it becomes difficult to obtain
accurate measurements. One solution is to use graph with the larger squares
subdivided by very small incremental markings. These very small markings
allow more accurate measurements. Although this is a better plan, there
is still the problem that the student is not able to see exactly where
the paper is being placed because the paper is opaque.
What students need in working with these small graphs
is a tool that
-
is light and small enough to work with,
-
has sufficiently small incremental markings,
-
has a straight edge for drawing lines,
-
allows the student to see though to the work below,
-
allows easy positioning for accurate measurements,
-
is easy to read,
-
costs less as students will be using it.
To meet these needs the one of the authors has developed
a device called "square ruler". This is a small (21/2
inch square) plastic template made with overhead transparency. On the boundary
there are small markings with numbers for quick counting of units. The
markings can be colored for easy reading and distinguish the material underneath
from the information on the square ruler.
This instrument was used in calculus classes extensively
in conjunction with the text book titled calculus concepts (see
[ 1]) in which most of the questions are dealt with graphs
rather than algebraic expressions. This instrument was small enough that
the students carried it inside a calculator case.
2 Square ruler
The following shows the square ruler (actual size). A unit on this boundary
is 1/2 inches and hence the distance between two
consecutive small tick marks is .05 inches.

One purpose of this method is to foster an awareness of scientific approaches
to solving problems. In early education, informal and intuitive measurement
is appropriate for inspiring students' natural curiosity. Students usually
measure objects with non- standardized units, such as hands or shoes. These
informal measuring methods shape young learners' basic mathematical sense
and make their mathematical experiences fun. As students continue to explore
mathematical concepts and ideas, they gradually discover the necessity
of standard units, especially in higher education. A scientific approach
to measurement plays a crucial role in problem solving, communicating and
reasoning.
Another purpose of using this square ruler is to help
students develop a mathematical way of thinking. This aims at reinforcing
the power of mathematics, building desirable attitudes toward learning.
It nourishes a logical mode of thought that is fundamental to mathematical
discovery and creation.
Thus the approach to measurement we discuss here not
only helps students make reasonably accurate estimations, but also helps
them better understand mathematical concepts and ideas.
We use this tool first to estimate units on the x-
and y-axes in terms of units on our square ruler (one unit in our
square ruler is .5in). We can estimate the coordinates of a point in terms
of units on our square ruler and translate these numbers to actual coordinates
on the graph. We can also estimate slopes of (tangent or secant) lines
and distances between two points.
3 Estimating scales on axes
Let us use this tool to estimate units on the x- and y-axes
in terms of units on our square ruler. Consider the following graph.
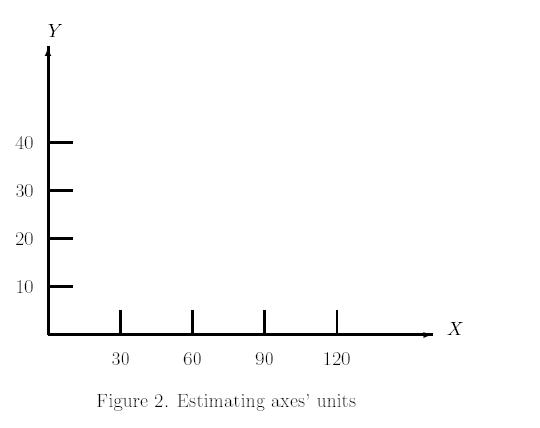
-
Step 1:
-
Place the square ruler on top of the graph. Align its borders with the
axes of the graph. Note that the grid on the square ruler makes it easier
to recognize any misalignment of the square ruler on the graph and to adjust
the square ruler so that the verticle lines are parallel with y-axis
and the horizontal lines parallel with x-axis.
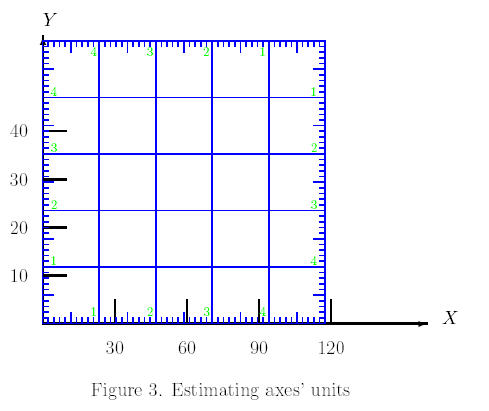
-
-
Step 2:
-
Read the distance on our square ruler between the marking 0 and 10 of the
given graph. In this case, the distance is .85. Thus 10 units on the y-axis
are equal to .85 units on our square ruler. Hence, one unit on our square
ruler is [10/ .85] = 11.76470588 units on y-axis.
Read the distance on our square ruler between the
number 0 and 30. In this case, the distance is 1.29. Thus 30 units on x-axis
are equal to 1.29 units on our square ruler. Hence, one unit on our square
ruler is [30/ 1.29] = 23.25581395 units on x-axis.
Most of the time it is better to estimate units on
our square ruler in terms of units on axes of the graph. However, the above
process also gives us units on the graph in terms of inches. For example,
10 units on the y-axis are equal to .85 units on our square ruler. This
means one unit on the y-axis is equal to [.85/ 10].5 = .0425inches.
Similarly, one unit on x-axis is [1.29/ 30].5 = .0215inches.
4 Estimating Coordinates
Consider the following graph. Let us estimate the coordinates of the point
A
as accurately as possible.
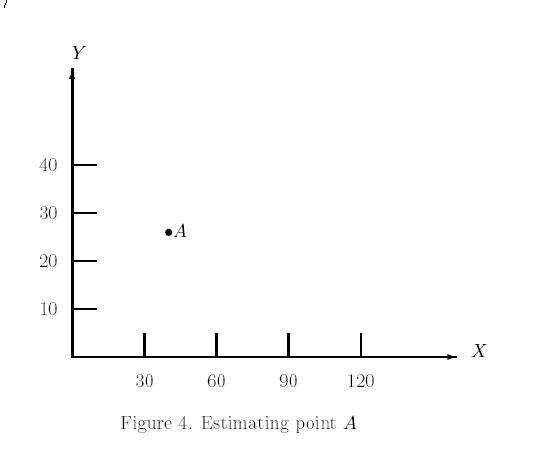
-
Step 1:
-
Estimate the units on axes as described in the previous section: One unit
on our square ruler is [10/ .85] = 11.76470588 units on y-axis and
[30/ 1.29] = 23.25581395 units on x-axis.
-
Step 2:
-
Place one corner of the square ruler at the point A, keeping the
vertical lines on the square ruler parallel to the y-axis of the graph
and the horizontal lines on the square ruler parallel to its x-axis.
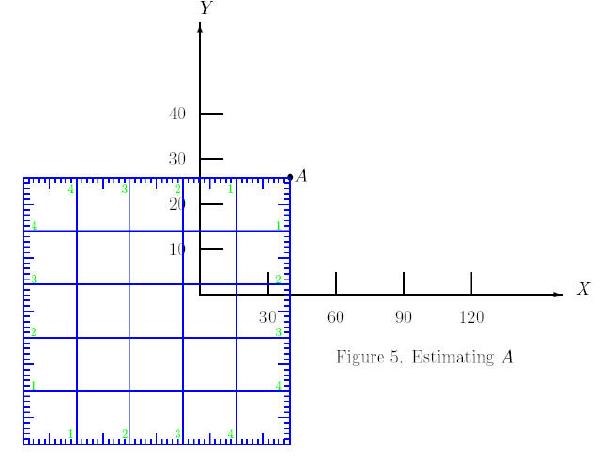
-
Step 3:
-
Read the distance on our square ruler between the y-axis and A.
In this case, the distance is 1.7. Thus the x-coordinate of A
is [30/ 1.29]1.7 = 39.53488372.
-
Step 4:
-
Read the distance on our square ruler between the x-axis and A.
In this case, the distance is 2.2. Thus y-coordinate of A
is [10/ .85]2.2 = 25.88235394.
Thus A = (39.53,25.88).
5 Estimating distance
Consider the following graph. Let us estimate the distance between points
A
and B.
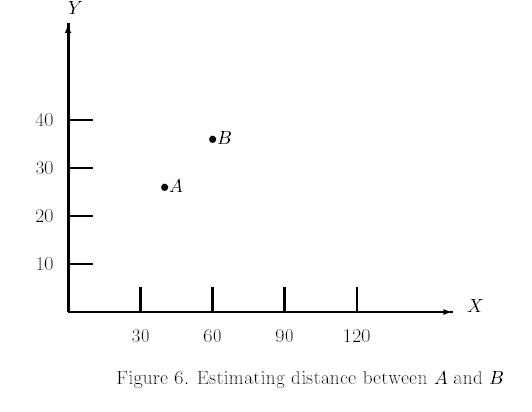
-
Step 1:
-
Estimate the units on axes as described in the previous section: One unit
on our square ruler is [10/ .85] = 11.76470588 units on y-axis and
[30/ 1.29] = 23.25581395 units on x-axis.
-
Step 2:
-
Place the square ruler in such a way that one point is on the vertical
side and the other point is on the horizontal side, keeping the vertical
lines on the square ruler parallel to the y-axis of the graph and
the horizontal lines on the square ruler parallel to its x-axis.
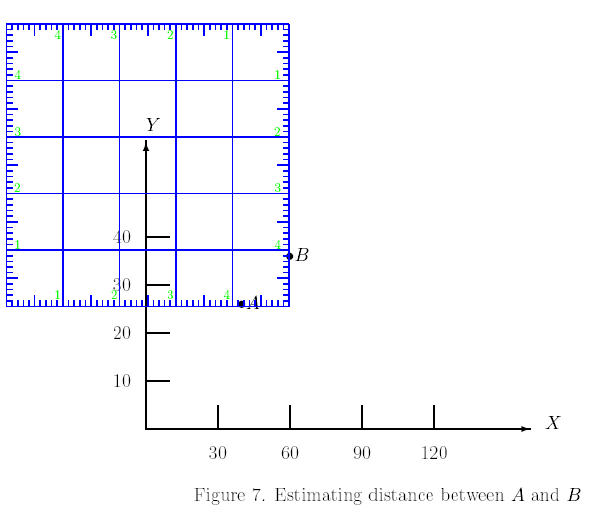
-
-
Step 3:
-
Read the distances on our square ruler between these points and the intersecting
corner. (If the square ruler is not wide enough, draw a line between A
and B and split the line into parts which can be measured separately
and add these measurements.) In this case, the distance for A is
.85 and for B is .9. Thus the distance between A and B
is Ö{(.85×[10/ .85])2+(.9×[30/
1.29])2} = 24.86764967.
Thus the distance between A and B is
24.87.
6 Estimating Slopes
We can use square ruler to estimate slopes of lines. Because of the properties
of lines, we can find the slope of a given line by computing slope of a
line either parallel or perpendicular to the given line. Our square ruler
contains several parallel and perpendicular lines that can be used effectively.
6.1 Slope of a line
Consider the following graph to estimate the slope of the line in the graph.
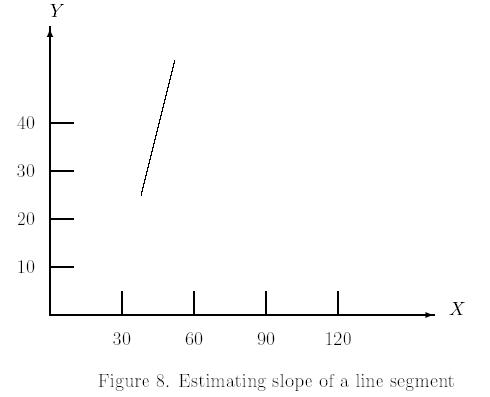
We first estimate the slope on our square ruler. Place
the square ruler on the graph, keeping the vertical lines on the square
ruler parallel to the y-axis of the graph and the horizontal lines
on the square ruler parallel to its x-axis, in such a way that the
line meets one horizontal and one vertical side of the square ruler.
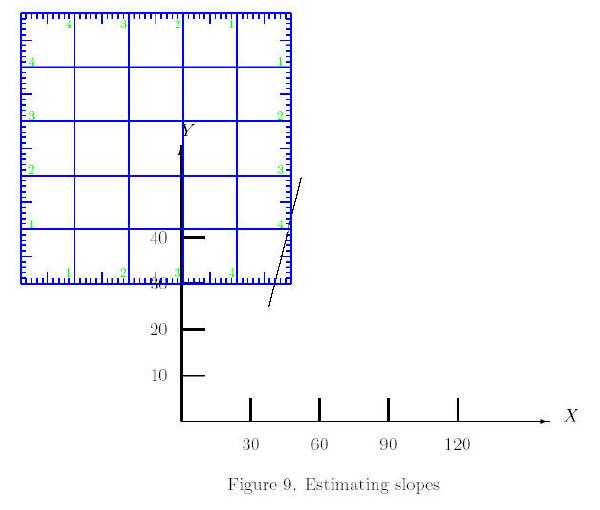
Since line meets the vertical side of the square ruler at 1.2 and the
horizontal side of the square ruler at .3, the slope is [1.2/ .3] = 4 with
respect to the units on the square ruler. Since we already know, one unit
on our square ruler is [10/ .85] units on y-axis and [30/ 1.29]
units on x-axis, the slope of the line on the graph is 4×[([10/
.85])/( [30/ 1.29])] = 2.023529412. Thus the slope of the line on the graph
is 2.02.
6.2 Perpendicular lines
We need to use caution when finding slopes of perpendicular
lines for a given line. If the unit lengths on both x- and y-axes
agree, perpendicular lines with respect to our square ruler agree with
those with respect to the coordinate system on the graph. For instance,
consider the following graph.
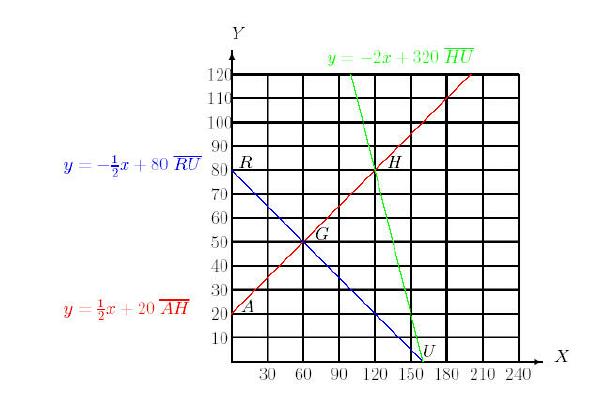
Different scales on axes make it difficult to judge whether two lines
are perpendicular by visual inspection. Note that the red ([`AH],
y = 1/2x+20) and green ([`HU],
y = -2x+320) lines are perpendicular. The red ([`AH],
y = 1/2x+20) and blue ([`RU],
y
= -1/2x+80) lines are not perpendicular inspite
of their appearance.
Now, consider the previous problem. Let us try to use
perpendicular lines to find the slope of the given line.
We align our square ruler in such a way that one of
the lines overlap on the given line. Note x- and y- intercepts
(A and B, respectively) of a perpendicular line.
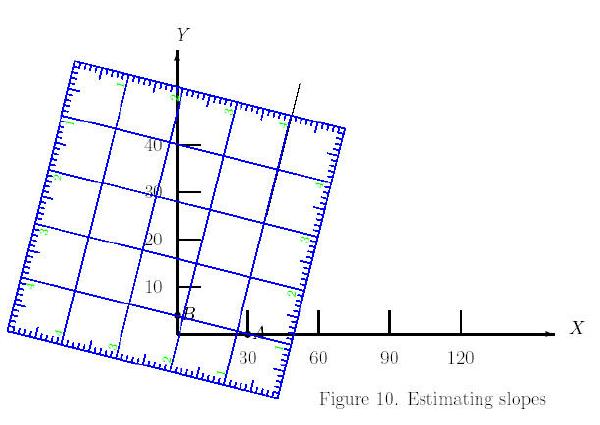
Now find the coordinates of these points as before by
aligning the square ruler with the coordinate system.
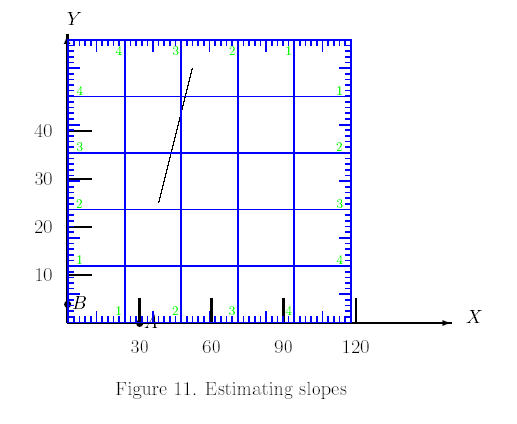
Note the A = (30,0) and B = (0,3.8) The line joining A
and B is perpendicular to the orignal line in the coordinate system
with respect to our square ruler. Hence the original slope is [30/ 3.8]×([([10/
.85])/( [30/ 1.29])])2 ~ 2.02.
6.3 Slope of the line segment between two
points
Consider the graph in section 5. In order to estimate
the slope of the line joining the points A and B, let us
repeat the process outlined in section 5 to find that the distance for
A
is .85 and for B is .9 (see Figure 9). Thus the
slope of the line joining A and B is [(.9×[30/ 1.29])/(
.85×[10/ .85])] = 2.090232568.
6.4 Tangent lines
Many students were reluctant to draw a tangent line
not sure of several considerations that go into drawing a tangent line.
The author has included some sample tangent lines on square ruler to give
the student some concrete examples of tangent lines. These tangent lines
can also be used in drawing tangent lines of curves. Here is the square
ruler with sample tangent lines.

The idea is to align one of these arcs with the part of the graph that
is around the point where one needs to find a tangent line. Then one can
use square ruler lines to figure out the slope. Let us consider the following
graph. Let us estimate slope of the tangent line at point marked as ·.
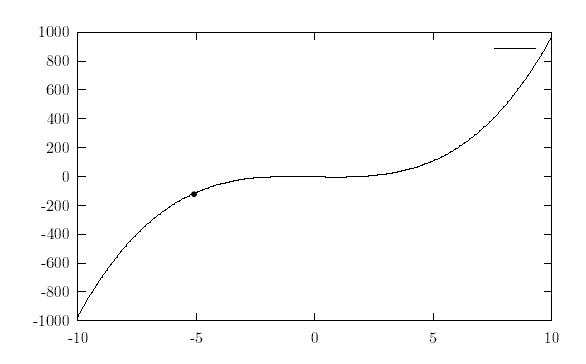
Choose an arc that is closest in shape around the point and place the
square ruler in such a way that the arc is aligned on the curve, Note that
the intersection point on the curve should match with the point of interest
on the graph.
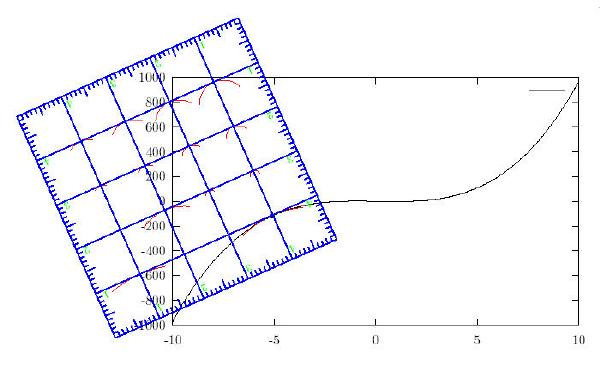
We can use any of the lines parallel to the tangent line to find the
slope. In this case, we can use the top line that meets borders of the
graph at (-10,800) and (-7.142,1000) (this point was estimated using the
method decribed above). Hence the slope of the tangent line is 69.9790063.
Notice that the accuracy of our measurements is limited
by the thickness of the points on the graph. For instance, if a point is
a circle with diameter more than .05 inches, then that point certains spans
over two consecutive markings on square ruler which clearly compromizes
the accuracy.
7 LATEX code
The reader, if interested, may be able to construct
square ruler. Here is a LATEX code the authors used
to print square ruler on a overhead transparency. After square ruler is
printed the edges must be cut very carefully to ensure straight edges on
all sides. The reader may also download this code, postscript file, dvi
file, or pdf file from the author's web page:
http://php.indiana.edu/
~ rgompa/estimate/estimate.htm
\documentclass[12pt]{article}
\usepackage{eepic}
\usepackage{color}
\begin{document}
\newcounter{foo}
\newcommand{\gadget}[2]{
\setlength{\unitlength}{.5in}
\begin{picture}(0,0)(#1,#2)
\thinlines
\scriptsize
\color{blue}
% verticle lines
\multiput(0,0)(1,0){6}{\line(0,1){5}}
% horizontal lines
\multiput(0,0)(0,1){6}{\line(1,0){5}}
% bottom
\multiput(0,0)(.1,0){50}{\line(0,1){.1}}
\multiput(0,0)(.5,0){10}{\line(0,1){.2}}
% top
\multiput(0,4.9)(.1,0){50}{\line(0,1){.1}}
\multiput(0,4.8)(.5,0){10}{\line(0,1){.2}}
% left
\multiput(0,0)(0,.1){50}{\line(1,0){.1}}
\multiput(0,0)(0,.5){10}{\line(1,0){.2}}
% right
\multiput(4.9,0)(0,.1){50}{\line(1,0){.1}}
\multiput(4.8,0)(0,.5){10}{\line(1,0){.2}}
% numbers in green
\color{green}
% bottom numbers
\setcounter{foo}{1}
\multiput(.9,0.2)(1,0){4}{\makebox
(0,0){\arabic{foo}}\addtocounter{foo}{1}}
% top numbers
\setcounter{foo}{4}
\multiput(.9,4.8)(1,0){4}{\makebox
(0,0){\arabic{foo}}\addtocounter{foo}{-1}}
% left numbers
\setcounter{foo}{1}
\multiput(0.2,1.1)(0,1){4}{\makebox
(0,0){\arabic{foo}}\addtocounter{foo}{1}}
% right numbers
\setcounter{foo}{4}
\multiput(4.8,1.1)(0,1){4}{\makebox
(0,0){\arabic{foo}}\addtocounter{foo}{-1}}
%arcs in first line
\color{red}
\put(1,1.51){\arc{1}{.4}{2.7}}
\put(2,1.51){\arc{1}{.6}{2.5}}
\put(3,1.51){\arc{1}{.8}{2.3}}
\put(4,1.51){\arc{1}{1}{2.1}}
% arcs in Second line
\put(1,2.26){\arc{.5}{.4}{2.7}}
\put(2,2.26){\arc{.5}{.6}{2.5}}
\put(3,2.26){\arc{.5}{.8}{2.3}}
\put(4,2.26){\arc{.5}{1}{2.1}}
% arcs in Third line
\put(1,3.11){\arc{.2}{.2}{3.1}}
\put(2,3.11){\arc{0.2}{.4}{2.7}}
\put(3,4.01){\arc{2}{1}{2.1}}
% arcs in Fourth line
\put(1,6.01){\arc{4}{1.2}{1.9}}
\put(4,6.51){\arc{5.0}{1.3}{1.8}}
\color{black}
\end{picture}
}
% change the coordinates according to your convenience
\gadget{2}{2}
\end{document}
8 Acknowledgements
The authors wish to thank all their calculus students, especially Patricia
Bowser, Candy Cheung, and Hongyu Guan, who used the square ruler in the
class and made very helpful suggestions and remarks. The authors would
like to thank Dr. Dominic Lopes for his helpful suggestions in writing
this paper.
9 References
-
1.
-
Latorre, Kenelly, Fetta, Carpenter, and Harris, Calculus Concepts, An
Informal Approach to the Mathematics of Change, brief first edition,
Houghton Mifflin, 1998.
-
2.
-
K. Yashiwara, B. Yashiwara, I. Drooyan, Modeling, Functions, and Graphs,
Algebra for College Students, second edition, Brooks/Cole Publishing
Company, 1996.
|