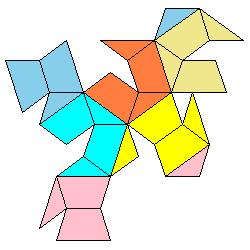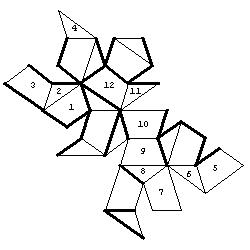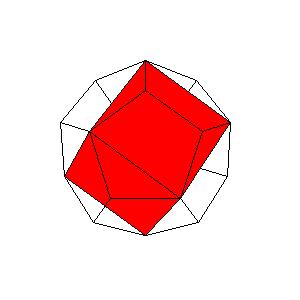
1. Euclid's strategy for constructing a dodecahedron was to start with a cube and build a 'roof' shaped structure on each face.[The Thirteen Books of Euklid's Elements, translated by Thomas L. Heath, vol 3, Dover Publications, 1956, pg. 499]
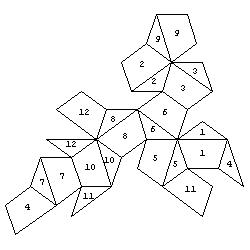
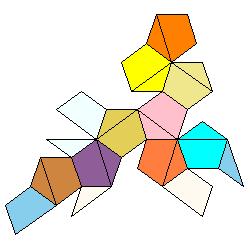
2. We now consider the dodecahedron as a solid with 24 faces, namely with 12 isosceles triangles and 12 trapezia. We may colour each of the 6 roofs by different colours or we may colour each of the 12 faces of the dodecahedron by different colours and then develop the surface of the polyhedron into a plane net.
3. In the first type of problem, a random net of the solid is given. The task is to colour the net so that the faces that belong to the same roof (or to the same face of the dodecahedron - the second type of problem), are coloured by the same colour.
Here a set of 60 problems can be downloaded.
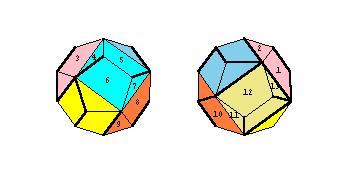
4. In the third problem the solid is given by two figures from two opposite viewpoints. There are also some walls along the edges of the solid. The task is to join two dots.
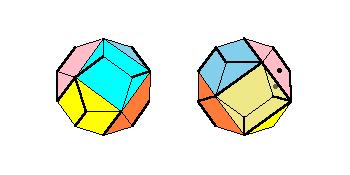
Here a set of 20 problems can be downloaded.
5. In the fourth problem a labyrinth on the solid is given, but this time the surface is developed into a plane net.
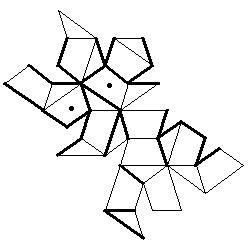
Here a set of 29 problems can be downloaded.
Solutions: