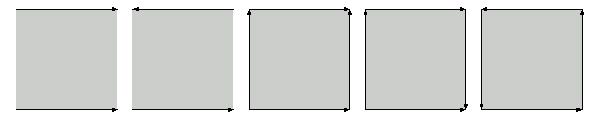
1. "There are useful topological descriptions of some elementary surfaces that are obtained from identifying edges in
a square. For example, if we identify the top and bottom edges of a square we obtain a cylinder. We describe this
identification by means of a square with an arrow along the top edge and an arrow pointing in the same direction
along the bottom edge. Now consider a square with the top and bottom edge identified, but in reverse order. We
indicate this identification by means of an arrow along the top edge and an arrow along the bottom edge pointing in
the opposite direction. The resulting surface is called a Möbius strip.
There are three possibilities when we identify the vertical as well as the horizontal edges of a square. If the vertical
arrows point in the same direction , and also the horizontal arrows point in the same direction, we obtain a torus. The
Klein bottle is the the surface that results when the edges of a square are identified with the vertical arrows pointing
in the same direction, but the horizontal arrows pointing in opposite directions. Clearly, the same surface results if we
interchange horizontal with vertical. Finally, the surface that results when we identify the edges of a square with both
the two vertical arrows pointing in the different directions and the two horizontal arrows pointing in the different
directions is called the real projective plane.
The above descriptions are topological. It is quite another matter to find parametrizations of these surfaces in
R3" [1].

2. To obtain a maze on a surface, we divide a square into smaller squares and define adjacency relation among the later, which means that two squares share common edge. This includes the identifications made above. In this way we get a graph. We find a random spanning tree and delete all edges that define adjacency on the tree. Remaining edges represent walls. We choose two circles and the task is to find the path from black to gray circle. So try to solve the mazes:
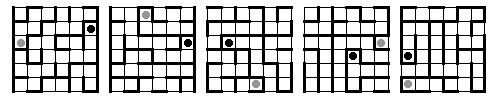
Here you will find about 30 problems, with solutions, of this type.
3. Now we want to make a maze on space surface. For this we need a parametrization of a surface. Definition. A patch or local surface is a differentiable mapping: U->R3, where U is an open subset of R2. Although the domain of definition of a patch can be any set, more often than not it is an open or closed rectangle [1] or even a unit square. For instance the standard parametrization of a sphere is given by sphere[a](u,v)=a(sinvcosu, sinvsinu, cosv). Here is an animation of a torus:
The following mazes on surfaces are of cylinder type with the exceptions of torus and Möbius strip. Mappings are used only to map vertices which are joined by straight lines. Red lines are "walls" of a maze.
4. Now a maze on a surface will be given by two views which cover the whole surface. In the case of the first five surfaces we shall take the front and the back view, in the case of the torus we take the top and the bottom view. We shall also remove some parts of a surface around poles. Try to solve the following mazes:
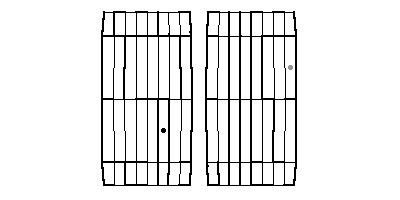
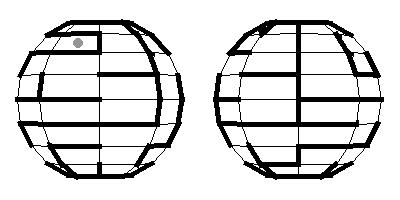
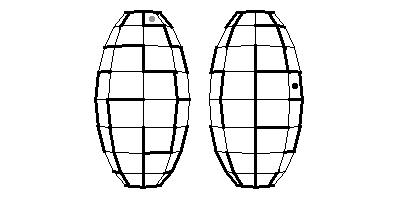
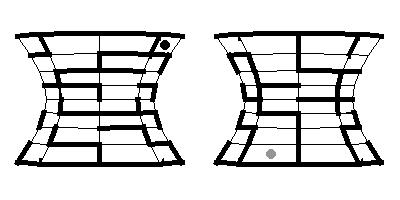
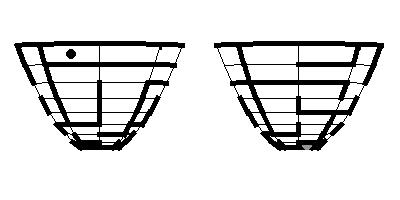
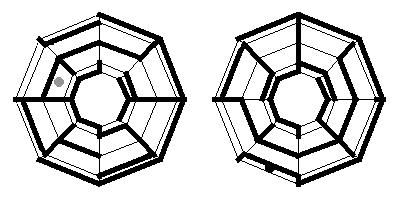
Here you will find about 50 problems of this type.
[1] A. Gray, Modern Differential Geometry of Curves and Surfaces, CRC Press, Boca Raton 1993.