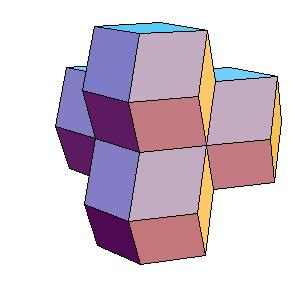
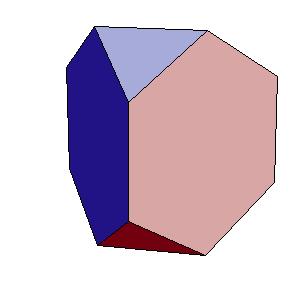
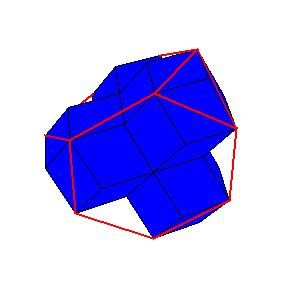
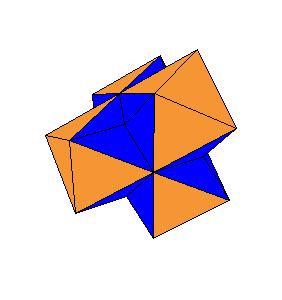
Dissection of rhombic 36-hedron to a tetrahedron and a truncated tetrahedron
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
Rhombic dodecahedron was discovered by Keper in 1611. He also showed that it could be
dissected to two cubes. From space filling by tetrahedra and truncated tetrahedra it follows
that these two solids together can be dissected to a cube, although individualy they could not be dissected to
a cube [3]. Result by A. Hanegraaf [2,pg.202], that two truncated octahedra can be dissected to a tetrahedron and a truncated tetrahedron
also show that the last two can be dissected to a cube.
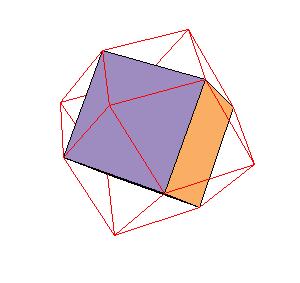
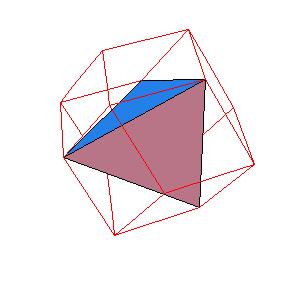
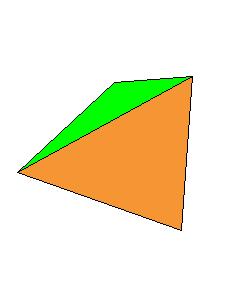
Our aim is to find for each of the solids the best approximation
by rhombic solids, that is, by solids generated by rhombic dodecahedron. Our result shows that a rhombic 36-hedron, a solid composed by four
rhombic dodecahedra can be dissected to a tetrahedron and a truncated tetrahedron. Since 4 rhombic dodecahedra can be dissected to 8 cubes, which
form a larger cube, this gives another proof for dissections of tetrahedra to a cube.
References
[1] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[2] G. N. Frederickson, Hinged Dissections:Swinging & Twisting, Cambridge U. Press, 2002.
[3] R. Williams, The Geometrical Foundation Of Natural Structure, Dover 1972