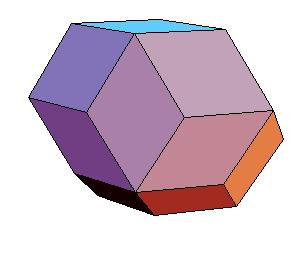
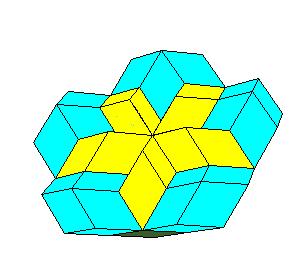
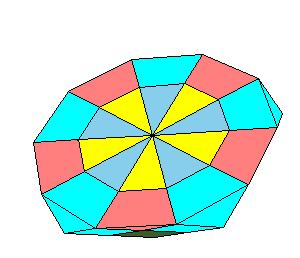
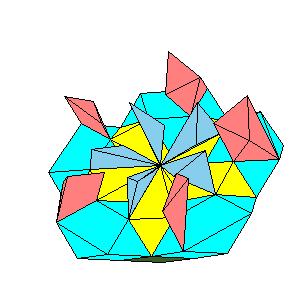
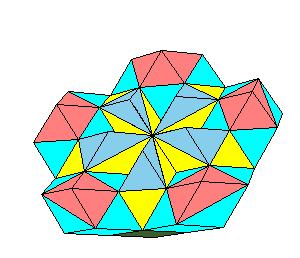
Hinged dissection of a half of rhombic icosahedron
Izidor Hafner
Tomislav Zitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25
, 1000 Ljubljana
, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
Rhombic icosahedron was first mentioned by Fedorov in
1885 [1]. It is composed of five prolate and five oblate rhombohedra,
or of one rhombic dodecahedron and three prolate and three oblate rhombohedra.
The half of rhombic icosahedron obtained by cut through pentad axis is easily
dissectable to a half of rhombic dodecahedron (of the second kind), and 3/2 of
prolate and oblate rhombohedra, and can be then dissected to
10 small cubes [2].
The problem is how to dissect the half of rhombic icosahedron obtained by the cut
orthogonal to pentad axis. Decompose the half of double rhombic icosahedron to
rhombic icosahedron, 5 dodecahedra, 5 prolate and 5 oblate rhombohedra. Then use hinged
dissections of dodecahera and prolate rhombohedra to
obtain the requested half of (double) icosahedron.
References
[1] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra - published in Visual Mathematics Vol.4, No.2, 2002, 2, (3)
[2] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube