
| 
| 
|
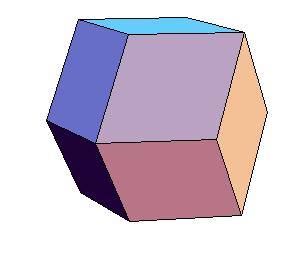
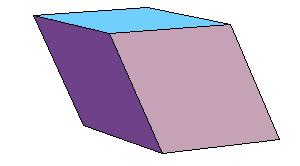
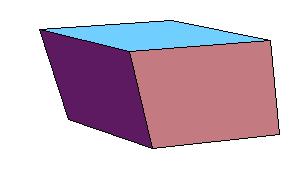
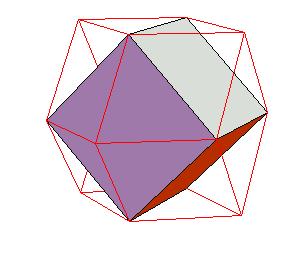
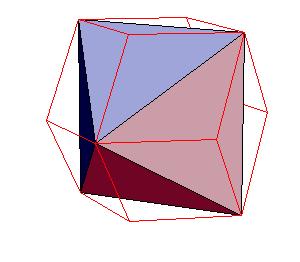
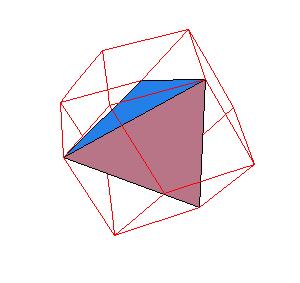
The next three ilustrations give the relation of rhombic dodecahedron to cube, octahedron and tetrahedron.
| 
| 
|
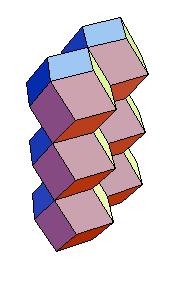
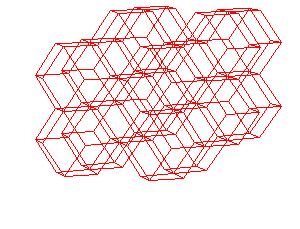
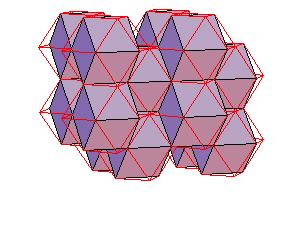
The rhombic dodecahedra fill the space.
| 
| 
| 
|
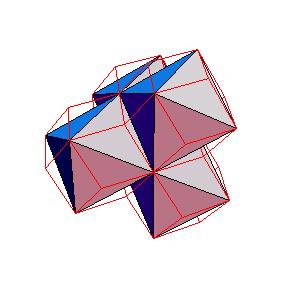
Join four dodecahedra along axes of threefold symmetry to obtain the following combination. To get similar figure use 12 oblate rhombohedra.
| 
|
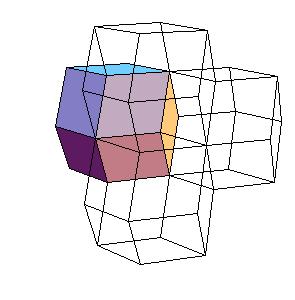
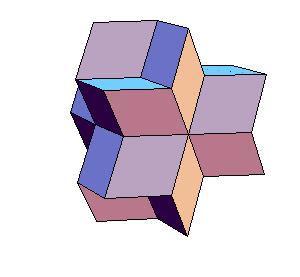
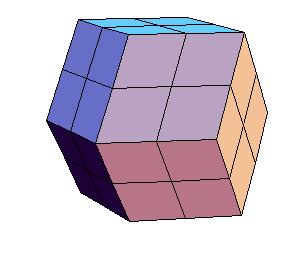
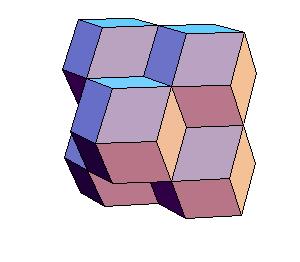
To make a double dodecahedron use 6 dodecahedra and 8 oblate rhombohedra.
| 
|
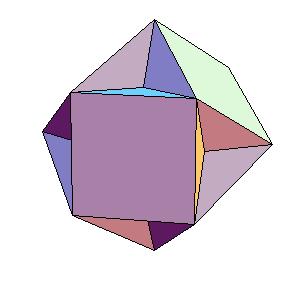
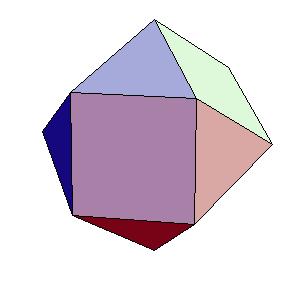
Take 6 halves of rhombic dodecahedra and 8 trianguar pyramids (1/4 of tetrahedra) to get cuboctahedron.
| 
|
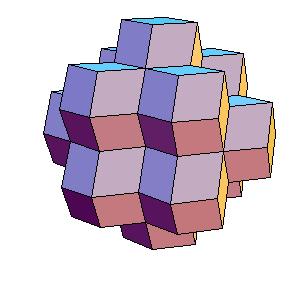
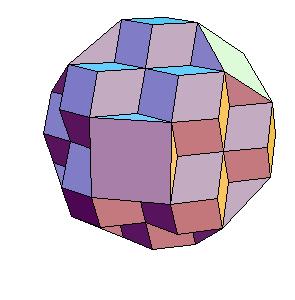
Put 12 dodecahedra on the dodecahedron. Put 6 halves of dodecahedron on poles of fourfold axes, level pyramids around threefold axes to get a truncated octahedron.
| 
|
To make models use the following nets
References
[1]
I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra