Dissections of golden rhombohedra
Izidor Hafner
Anja Komatar
Trzaska 25, 1000 Ljubljana, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
"A rhombohedron is a parallelepiped bounded by six congruent rhombs. It has two opposite vertices at which the three face-angles are equal; it is said to be acute or obtuse according to the nature of these angles. A golden rhombohedron has faces whose diagonals are in the golden ratio t : 1 " [1, pg. 161]. The volumes of A6 (the acute rhombohedron) and O6 (the obtuse rhombohedron ) are also in the ratio t : 1.
"The Fibonacci sequence 1, t, 1+t, 1+2t, 2+3t, 3+5t, 5+8t, 8+13t, is equal to geometric sequence 1, t, t2, t3, t4, t5, t6, t7"[2, pg. 94].
If we take the obtuse rhombohedron of volume 1, then the obtuse rhombohedron whose edges are t as long, has volume t3=1+2t. So there exists a dissection of tO6 to one O6 and two A6.
On the other hand the volume of tA6 is t4=2+3t, so there exists a dissection of the solid to two O6 and three A6.
But t4=t2+t3=t3+1+t, so there is a dissection of tA6 to tO6, O6 and A6.
Finaly we could dissect O6 to (1/t)O6 and two (1/t)A6.
In this paper we shall illustrate the dissection of tA6 to tO6, A6, (1/t)O6 and two (1/t)A6. (Or similar disection of t2A6 to t2O6, tA6, O6 and two A6. Observe: 8+13t = 5+8t + 3+5t = (5+8t) + (2+3t) + (2t) + 1.
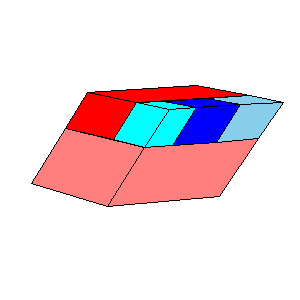
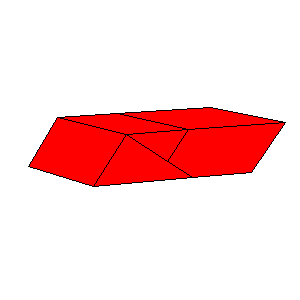
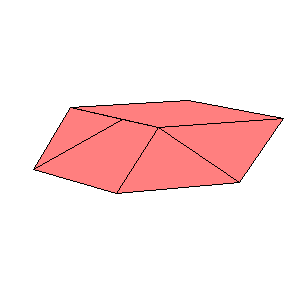
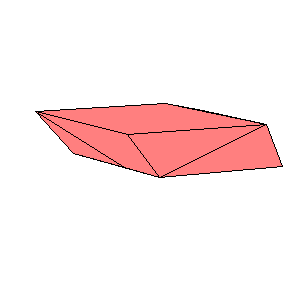
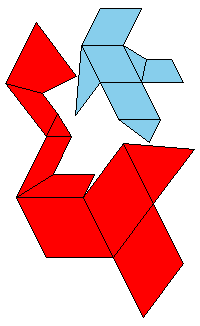
There is a three piece dissection of the red parallelepiped to A6. There is a four piece dissection of the pink parallelepiped to tO6. The blue and the gray parallelepipeds are (1/t)A6. The pink and the cyan parallelepipeds are similar, so there exists a four piece dissection of the cyan parallelepiped to (1/t)O6. Use the below nets to make a model. Since the pieces of the dissection of cyan parallelepiped are too small, it is given as a whole.
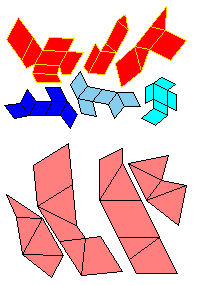
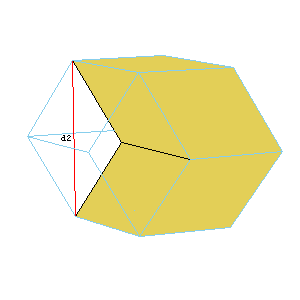
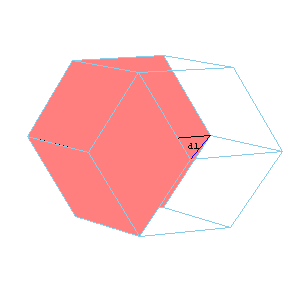
The visual proof that the volumes of A6 and O6 are in ratio t:1. The rhombic dodecahedron of the second kind can be dissected to two A6 and two O6. The area of the rhombus is d1d2/2. The hight of A6 is d2/2, and the hight of O6 is d1/2. So the ratio of volumes is d2 : d1 = t .
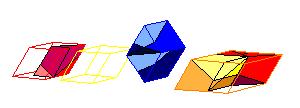
To make a model of the combination of A6 and tO6 use the nets below. Observe that A6 has the same hight as tO6. So, the ratio of hights of A6 and O6 is (ones again) t .
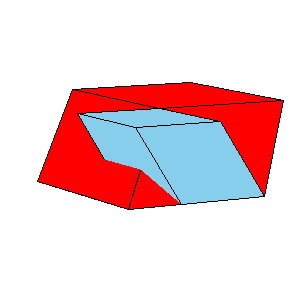
A dissection of two A6 and one O6 to tO6 given below will be explained in another paper.
References
[1] W.W. Rouse Ball, H.S.M. Coxeter, Mathematical recreations and essays, Thirteen Edition, Dover Pub., 1987.
[2] M. Gardner, AHA! Gotcha, Paradoxes to Puzzle and Delight (Slovenian eddition), 1992
[3] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra, http://www.mi.sanu.ac.yu/vismath/hafner2/IntrodRhombic.html