
|
| 
| 
| 
|
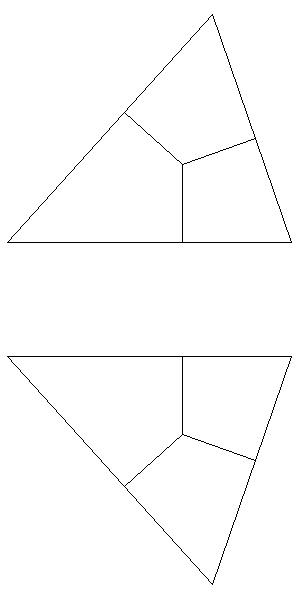
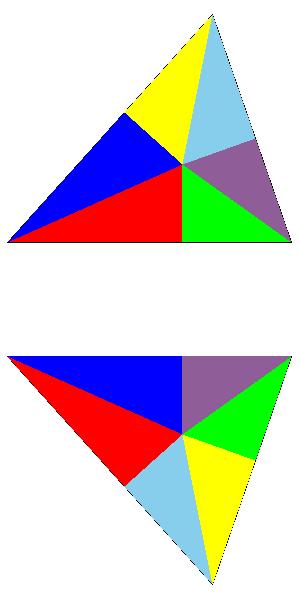
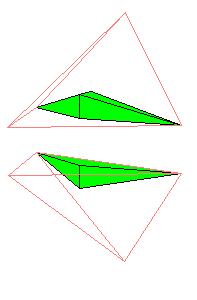
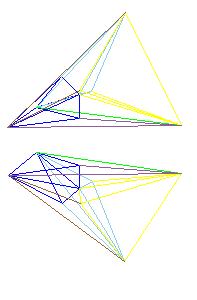
Note that pieces are moved in the plane of the triangle (the third and the fourth figure) and not through rotation in space as is indicated by the second figure.
| 
|
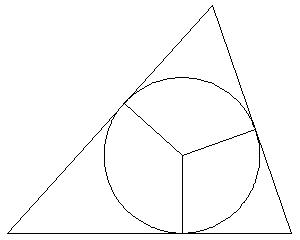
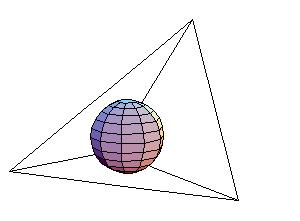
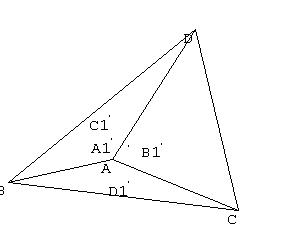
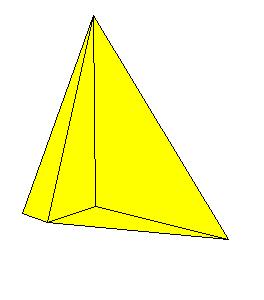
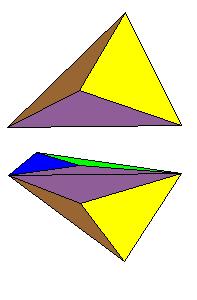
First, inscribe the sphere in the tetrahedron. The point of tangency with the face opposite vertex A is A1, with B1, C1, and D1 similarly named. Next cut the tetrahedron into six pieces [1, pg. 232].
| 
|
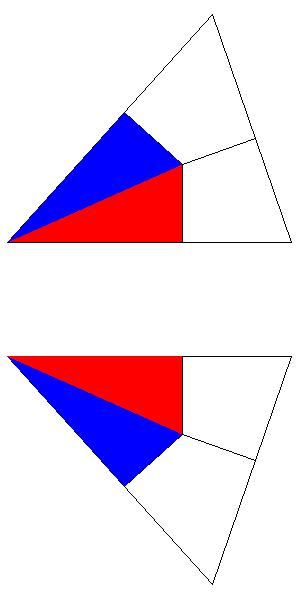
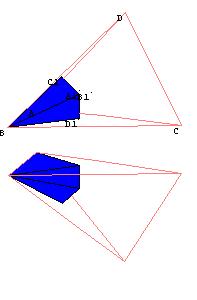
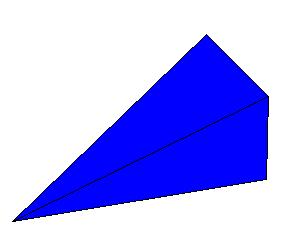
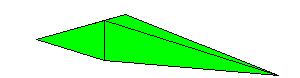
The upper figure shows the piece that belongs to edge AB. The other vertices being the points of tangency C1 and D1 and the center of the inscribed sphere. Here are two more pieces and the final construction:
| 
| 
|
| 
|
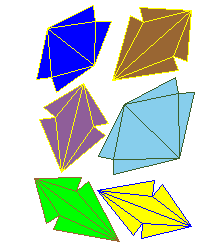
Use the following nets to make models. Note that nets are symmetrical (Aleksandrov theorem: a symmetrical polyhedron has a symmetrical net ).
|
References
[1] Frederickson G. N., Dissections: Plane & Fancy, Cambridge University Press 1997.
[2] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html.