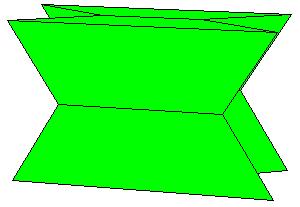
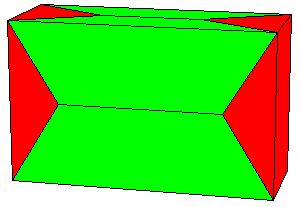

| 
|

| 
|

| 
|
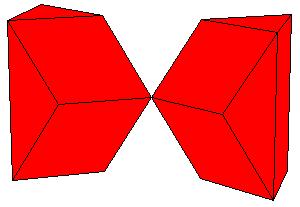
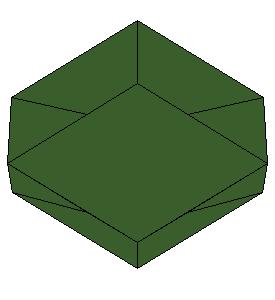
The obtained rectangular brick already has one appropriate dimension so we need only one P-slide to get a cube[1., pg.33].
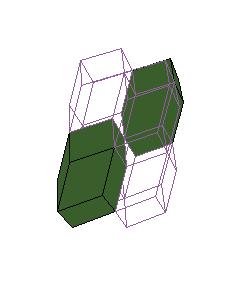
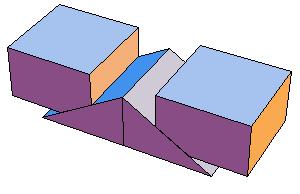
But we wish to get a symmetric dissection using one dodecahedron and eights of the other.
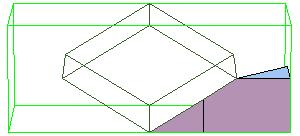
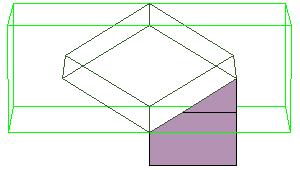
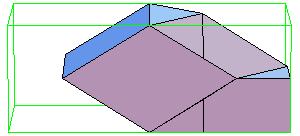
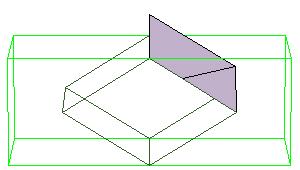
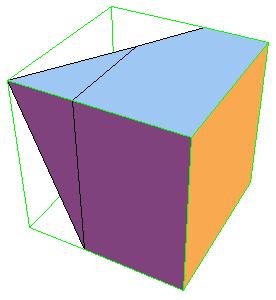
Essentially we repeat P-slide eight times.
Some of the intermediate steps are v given below.
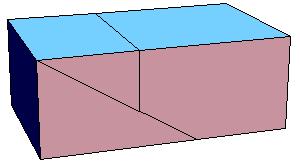
| 
|
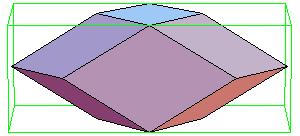
| 
|
| 
|
| 
|
| 
|
| 
|
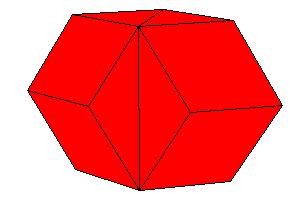
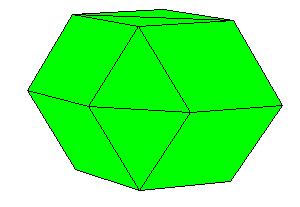
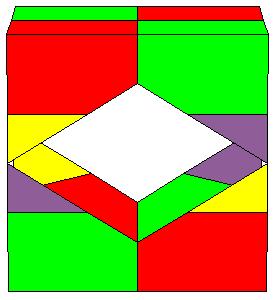
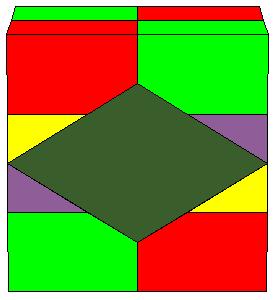
To make a paper model of a cube 2 copies of the following nets are needed together with a calibrated net of a rhombic prism.
References
| [1] | G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997, |
| [2] | I. Hafner, T. Zitko, From dissection of the cube to space filling with prolate rhombohedra and rhombic dodecahedra of the second kind - published in Visual Mathematics Vol.4, No.2, 2002, 2, (5). |