Abstract
Visual construction of a dissection of a rhombic solid to a combination of the truncated dodecahedron and the icosahedron is given.
Introduction
The authors of [1, pg. 331] produced the table of the Dehn invariants for the non-snub unit edge Archimedean polyhedra. Let us take only icosahedral part:
Icosahedron 60(3)5
Dodecahedron -30(5)1
Icosidodecahedron -60(3)5+30(5)1
Rhombicosidodecahedron 60(3)5-30(5)1
Truncated icosahedron 30(5)1
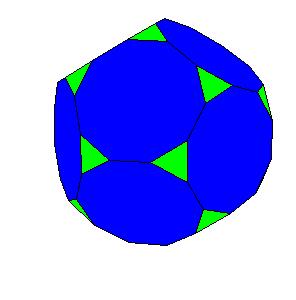
Truncated dodecahedron -60(3)5
Truncated icosidodecahedron 0
From this table the following combinations with sum 0 exist.
Truncated icosidodecahedron
Icosahedron+ Truncated dodecahedron
Dodecahedron+ Truncated icosahedron
Icosahedron+ Dodecahedron+ Icosidodecahedron
Icosidodecahedron+ Rhombicosidodecahedron
Truncated icosahedron+ Truncated dodecahedron+ Rhombicosidodecahedron
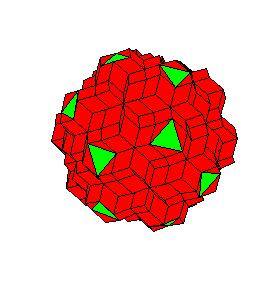
For each of the above combinations we found an equidecomposable combination of rhombic solids [7]. By rhombic solid we mean a polyhedron that consists of prolate and oblate golden rhombohedra. In the solution we use also halves of rhombic dodecahedron of the second kind [4], which in turn consists of two rhombohedra. It is obvious, that rhombic solids can be dissected to a cube. The idea is to find the best “approximate” of an Archimedean solid by a rhombic solid. In fact there are basically two solutions depending on the length of edges of the Archimedean solid, which may be shorter or larger diagonal of the rhombus (although the larger edges are also possible). Each Archimedean solid has a surplus or a deficit relative its approximate. We found examples where only two types of solids appear as difference:
For the first family they are a pentagonal pyramid (P5) that can be cut off triacontahedron and triangular pyramid, that is 1/20 of the icosahedron (P3A). For the second family they are pentagonal cup (or cap)(C5) and a triangular pyramid cut off oblate rhombohedron (P3B).

| 
|

| 
|
Archimedean solids and their surplus and (or) deficit are given by tables (we treated icosahedron in the first table in relation to empty set):
| Solid | Deficit | Surplus | |
| Icosahedron | 20P3A | ||
| Dodecahedron | 12P5 | ||
| Icosidodecahedron | 20P3A | 12P5 | |
| Rhombicosidodecahedron | 12P5 | 20P3A | |
| Truncated icosahedron | 12P5 | ||
| Truncated dodecahedron | 20P3A | ||
| Truncated icosidodecahedron |
| Solid | Deficit | Surplus | |
| Icosahedron | 20P3B | ||
| Dodecahedron | 12C5 | ||
| Icosidodecahedron | 12C5 | 20P3B | |
| Rhombicosidodecahedron | 20P3B | 12C5 | |
| Truncated icosahedron | 12C5 | ||
| Truncated dodecahedron | 20P3B | ||
| Truncated icosidodecahedron |
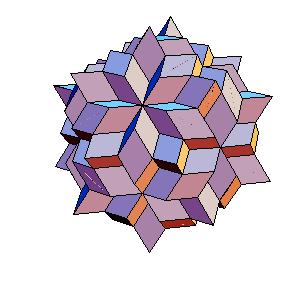
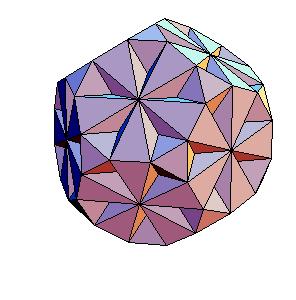
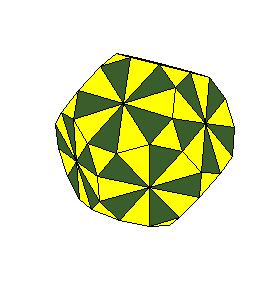
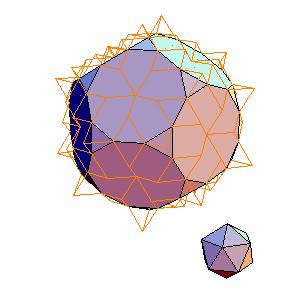
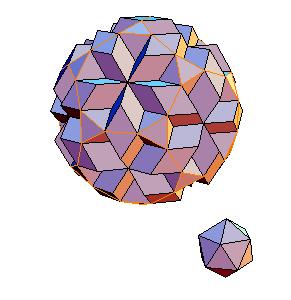
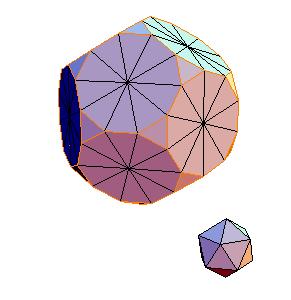
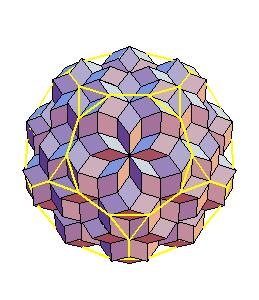
The dissection of a rhombic 210-hedron [6] to the combination of the truncated dodecahedron and the icosahedron is the most obvious one in case the edge equals the smaller diagonal. Namely, if we cut off 20 spikes at the poles of triad symmetry, they form the icosahedron. The remaining concave and convex pyramidal forms at poles od pentad symmetry annihilate one onother.
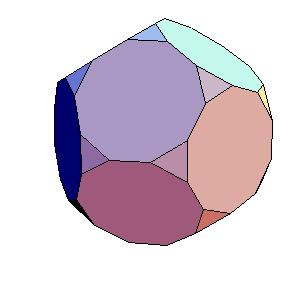
| 
| 
|
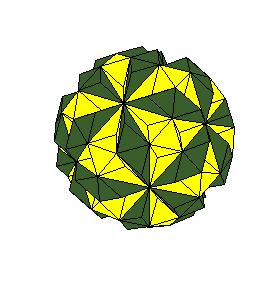
| 
| 
|
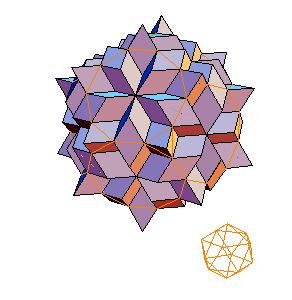
| 
| 
|
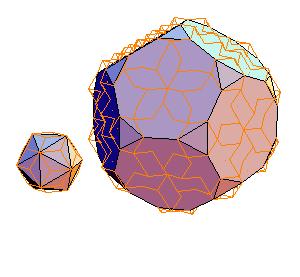
Equidecomposable combinations, edge equals the larger diagonal:
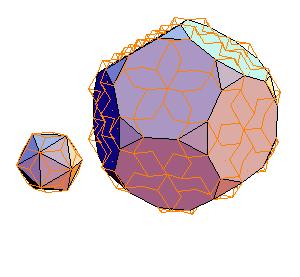
| 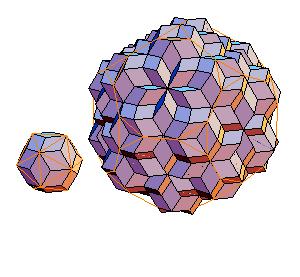
| 
|
| 
| 
|
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are
rational, Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] G. N. Frederickson, Dissections: Plane & Fancy, Cambridge U. Press, 1997.
[3] I. Hafner, T. Zitko, A dissection of quarter of rhombic dodecahedron of the second kind to a cube, http://torina.fe.uni-lj.si/~izidor/RhombicPolyhedra/RhombicPolyhedra.html
[4] I. Hafner, T. Zitko, Introduction to golden rhombic polyhedra
- published in Visual Mathematics Vol.4, No.2, 2002, 2, (3)
[5] I. Hafner, T. Zitko, Relations among rhombic, Platonic and Archimedean solids
- published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[6] I. Hafner, B. Jurcic-Zlobec, T. Zitko, Gallery of rhombic polyhedra, - published in Visual Mathematics Vol.4, No.2, 2002, 2, (4)
[7] I. Hafner, Live3D Animation to Solution of Conway-Radin-Sadun problem, Visual Mathematics, Volume 9, No. 1, 2007 ,1