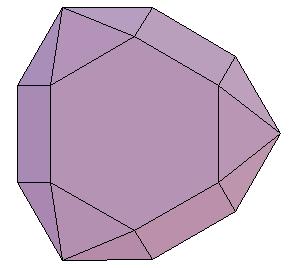

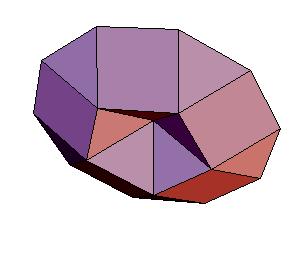
We observed the following facts: triangular hebesphenorutunda (Johnson solid 92) and Steward toroid G3 can be together dissected to a combination of rhombic solids, drilled pentagonal gyrobicupola can be dissected to a rhombic solid. Click on the picture to activate Live3D graphics [3].

| 
| 
|
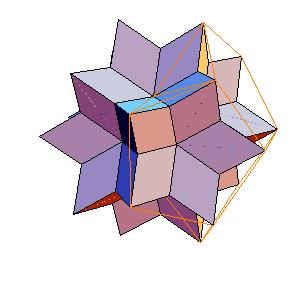
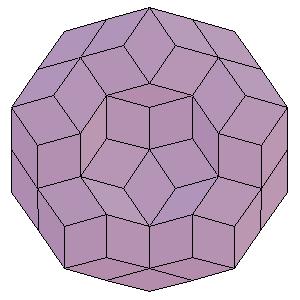
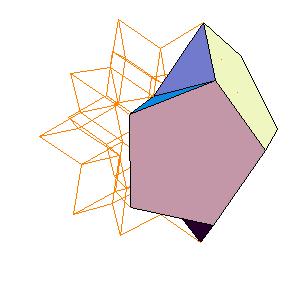
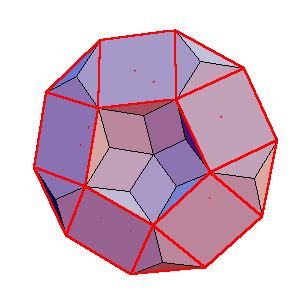
To derive the coordinates of the solids we use the following rhombic polyhedra:
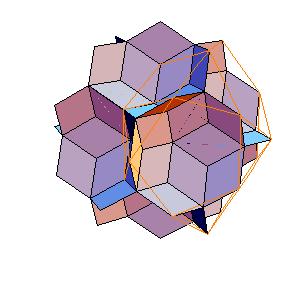
| 
| 
|
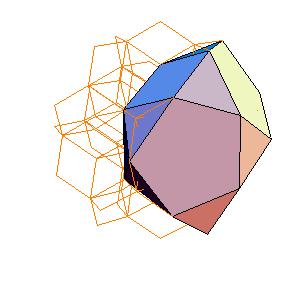
| 
| 
|
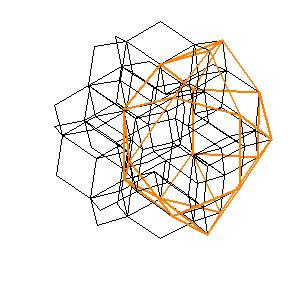
| 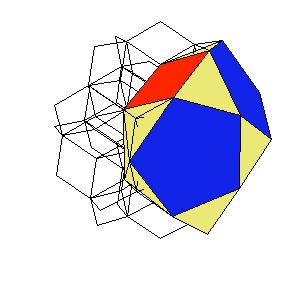
| 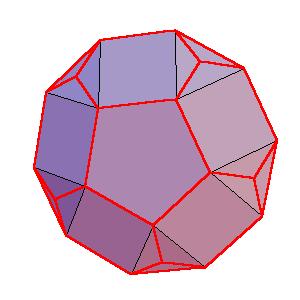
|
We also made a real model of a rhombic solid that aproximate J92 (3 halves of rhombic dodecahedron of the second kind should be added):

To aproximate the first two solids we need 35
prolate rhombohedra and 21 oblate rhombohedra.
As far as drilled pentagonal gyrobicupolais is concerned,
we observed that the rhombic aproximate has neither
surplus nor deficit, so they are equidecomposable.
The rhombic solid consists of 10 prolate rhombohedra and
5 rhombic dodecahedra of the second kind.
We see that drilled pentagonal gyrobicupola
consists of 10 congruent skew triangular prisms.
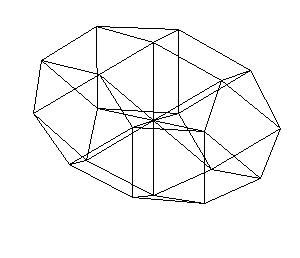
|
The method of counting surplus and deficit [1,2] of a solid relative to its
rhombic aproximate is applied to get a table for the solids.
The part we count are:
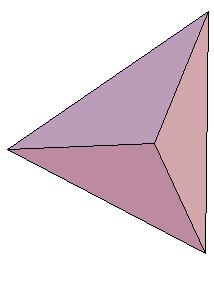
pentagonal cup (or cap)(C5) and
a triangular pyramid cut off oblate rhombohedron (P3).
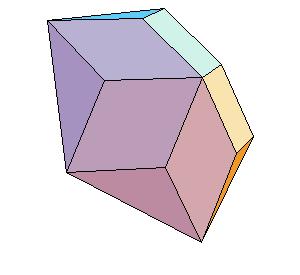
| 
|
| pentagonal gyrobicupola (J31) | +2C5-10P3 |
| triangular hebesphenorutunda (J92) | -3C5-5P3 |
| drilled pentagonal gyrobicupola | 0 |
| Steward toroid G3 | +3C5+5P3 |
References
[1] I. Hafner, Live3D Animation to Solution of Conway-Radin-Sadun problem, Visual Mathematics, Volume 9, No. 1, 2007 ,1
[2] I. Hafner, Dissection of a rhombic solid to the trucated dodecahedron and the icosahedron
[3] Martin Kraus' Live3D applet http://www.vis.uni-stuttgart.de/~kraus/index.html