Paper Model Solution of Conway-Radin-Sadun Problem
Izidor Hafner
Tomislav Žitko
Faculty of Electrical Engineering, University of Ljubljana
Trzaska 25, 1000 Ljubljana, Slovenia
e-mail: izidor.hafner@fe.uni-lj.si
In the article we provide nets for paper models of polyhedra connected
with the proof of Conway-Radin-Sadun problem. In [1] J. H. Conway, C. Radin and L. Sadun applied
their theory of geodetic angles to the non-snub Archimedean polyhedra proving that some
combinations of Platonic and Archimedean solids can be decomposed to a cube.
In particular it was proved that it was possible to dissect the icosahedron, the
dodecahedron, and the icosidodecahedron into finitely many pieces that can be reassembled to form a large cube.
The problem is, how to perform such a dissection. In [2] an animated proof of how to dissect the icosahedron,
the dodecahedron, and the icosidodecahedron into finitely many pieces that can be reassembled to form the
rhombic triacontahedron and the rhombic hexecontahedron is given. The former consists of 10 oblate and 10 prolate
golden rhombohedra; the later consists of 20 prolate rhombohedra.
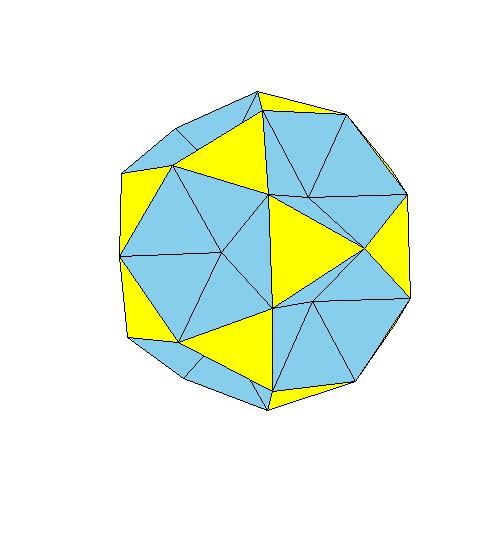
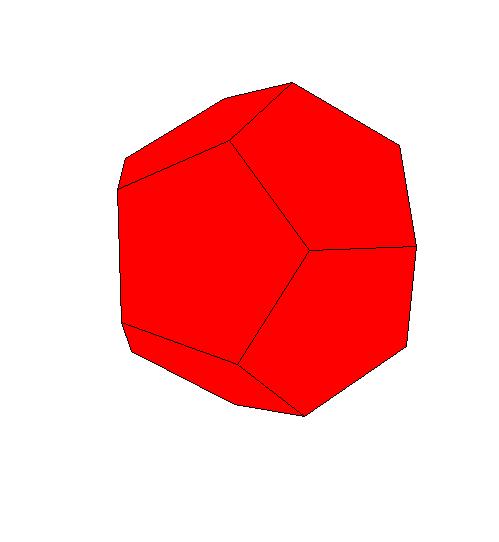
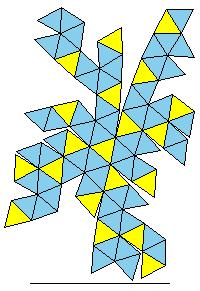
If we glue provided nets, we could make a concave 80-hedron, the regular dodecahedron, 20 triangular pyramids and 12 pentangular
pyramids. Note that yellow triangles are equilateral while blue ones are only isosceles.
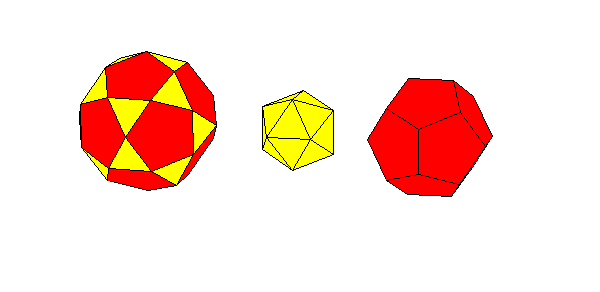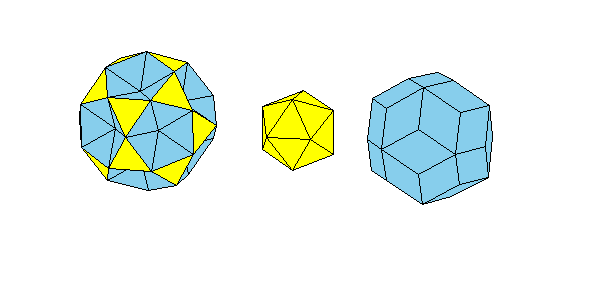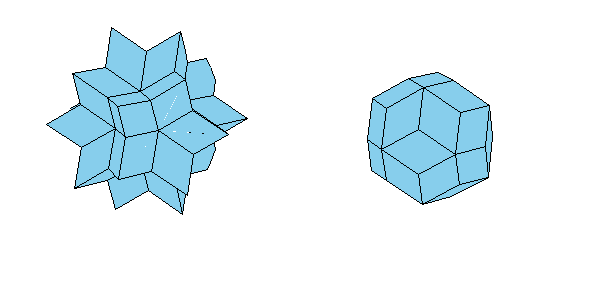
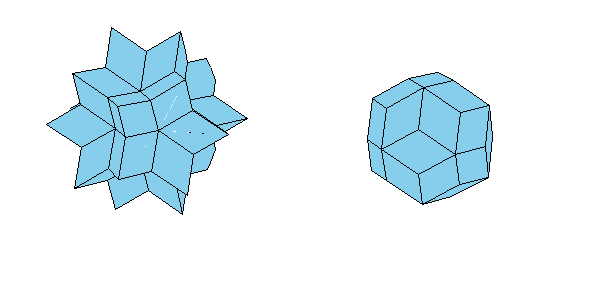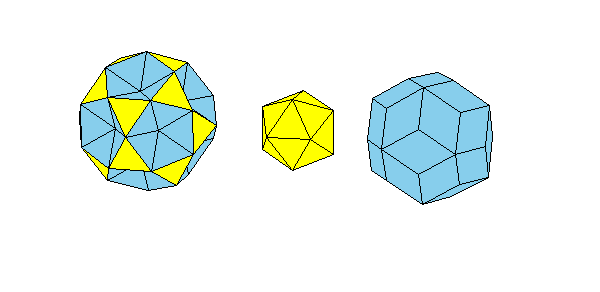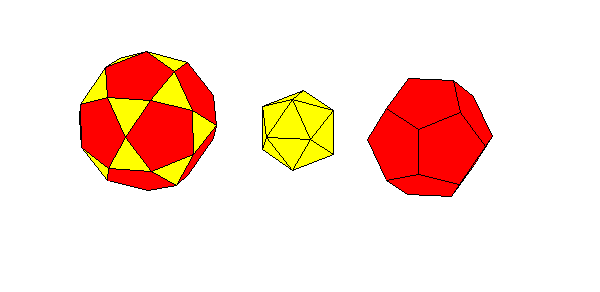
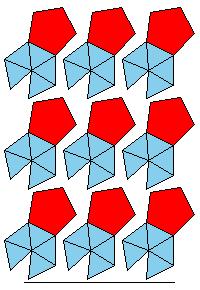
Form the icosahedron from 20 triangular pyramids and fill 12 concave parts of 80-hedron with pentagonal pyramids
to get icosidodecahedron:
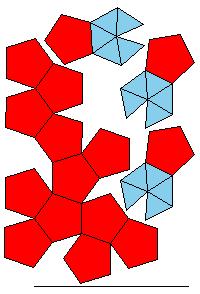
Or put 12 pentagonal pyramids on the dodecahedron to form the triacontahedron and put 20 triangular pyramids
on 80-hedron to get the hexecontahedron:
When printing the following nets make sure the bottom black line has the same length on each print.
References
[1] J. H. Conway, C. Radin, and L. Sadun, On angles whose squared trigonometric functions are rational,
Discrete & Computational Geometry, 22 (1999), pages 321-332.
[2] I. Hafner, Animated Proof of Conway-Radin-Sadun Problem