|
Bradford Hansen-Smith 4606 N. Elston #3 Chicago IL 60630, USA Abstract
Introduction The circle is much more than what we call it. Draw a circle. Cut out around the picture of the circle. You have in your hand a circle in space. This paper will explore the process of folding the paper circle. The circle is about movement patterns, and how the circle shape is reformed into traditional polyhedra and many non-traditional polyhedral forms and systems. There are examples of how, by joining multiples of circle-folded forms, systems of great complexity and diversity of forms can be generated. The focus is on the folding process that allows the creased circle to form and be reformed, changing the arrangements of the circle surface, forming interval spaces, and shifting between symmetries. The combinations of the curved edge of the circle disk and the straight lines from the folding process allows in-between combinations of forms that are not seen in any traditional means of geometric model making. Fundamental geometry and mathematical functions, such as theorems, formulas and basic equations, are demonstrated in the inherent relationships between the folded creases in the circle, which make folding circles a very useful teaching tool. That information is not the focus of this paper and will not be addressed except as it relates directly to the folding process. Before starting to fold the circle we must first understand that the circle is also the compression of the sphere to a flat plane. In that regard the circle holds all spherical information; all polyhedra, polygons, divisions of symmetry, and the spatial formations that are revealed by traditional cutting into the sphere. Because the circle is a compression of the sphere, folding the circle is a decompression, forming replications of spherical information in both 2-D and 3-D forms. The sphere is whole. Compression of the sphere is movement.
Decompression through folding is movement. I call this process of folding
the circle, Wholemovement; the movement of the whole to itself. There is
no need for cutting or measuring. The circle is self referencing to the
wholeness of the shape.
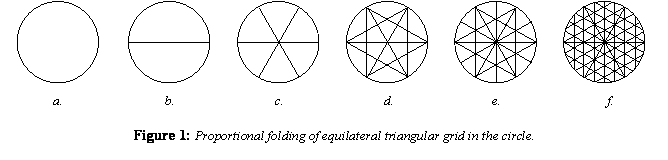
Folding the Circle Fig.1a) The circle. The folding procedure for the circle is inherent in the axial movement of the sphere. Fig.1b) Fold the circle diameter-axis by touching any two imagined points on the circumference exactly together and crease with a hard edged tool. This folds the circle in a ratio of one whole: two parts. Touching points and the 1:2 ratio are the only two directives that are needed for folding the rest of the circle. After folding the circle in half there are only three ways to proportionally fold the semi-circle in the ratio 1:2. Three folds yield 3 diameters, four folds yield 4 diameters, and five folds yield 5 diameters. We are concerned with only three diameters. If you know what three diameters do, then four and five do the same thing only in a different proportional symmetry to the division of the circumference. The symmetries are different and many of the forms and systems will be different than those of the three-six symmetry. The process is principled and is consistently the same patterns through out all reformations. Fig.1c) Fold the divided circle into thirds. Do this by folding one end over and the opposite end under with the third section in the middle. Eyeball this folding. Slide the sections back and forth to make all the curved and straight edges, and all three end points even. When everything is congruent, crease with a straight edge. Folding the circle in half and then into thirds can also be described as three folds in the ratio of 1:2. Open the circle out flat and observe three diameters equally spaced in a hexagon pattern. There are seven points, six are the end points of each diameter with one in the center. There are three individual points on each diameter. These seven points are the points of reference for all 3 diameter circle folding. Fig.1d) Fold one circumference point to the center point touching exactly. The diameter line will fold onto itself when the points are accurately placed. Then crease. Do this to each point of the six circumference points. This will form a creased hexagon star. Fig.1e) Fold the end point of one diameter to the opposite end point on the same diameter and crease. Do this to all three diameters. This will divide the circle into twelve equal sections showing another set of three diameters of a different divisional proportion. These I call bisecting diameters to differentiate them from the first three diameters (starpoints). The starpoint diameters are now divided into 4 equal segments. There are three sets of three parallel lines each at right angles to the first three diameters. Together the three sets of three lines form an equilateral triangle grid with three diameters bisecting all twelve completely formed equilateral triangles. I call this creased grid the 4-frequency diameter circle. Fig.1f) To fold a complete octave (similar to an octave in music) we use the same process of touching points. With each diameter, touch the circumference starpoints to the two new points of intersection on the same line. The new points are located by finding the inner hexagon shape and locating mid points on each side that lie on the three diameters (fig.1e). Using the end point of each diameter, touch to the closest point and crease, then touch and crease the opposite point on the same diameter. Each diameter is now divided into 8 equal sections increasing the triangle grid to an 8-frequency diameter circle.
The circle demonstrates a unique quality of wholeness
in that it can be reformed to model anything that can be formed by any
other polygon. The circumference can be reformed in ways not possible using
straight edges. The circle demonstrates absolute unity where all shapes
and forms are transformed one to another through movements of division
without separating anything from the circle. The whole circle when reformed
and joined in multiples to construct systems are then used as parts.
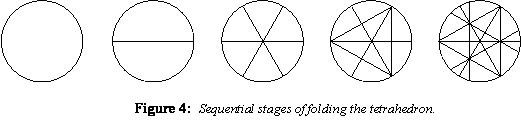
Examples of Folded Systems The following pictures show samples of systems that can be formed by reconfiguring the 24 creases of the 8-frequency folded grid circle. They are derived from the three folded diameters of the hexagon pattern. These are the same folded circle grid, the same geometry, and the same process of folding. One of the first forms in learning to fold the circle is the tetrahedron. It is primary pattern and comes first. In multiple progressive opening the tetrahedron will form the other four "Platonic Solids" showing the dual nature of each. The tetrahedron is first folded using just nine creases, Fig.4. Folding the tetrahedron using all 24 creases gives the greater potential for reforming and modifying the form.
Figure 2: 6 tetrahedra in a pentagon spiral
Figure 3: Pentagon spiral developed Fig.2) The spiral is formed by folding six tetrahedra and joining them face-to-face. Each joining of faces slid one half of the edge length, or one quarter of the surface area. This progressive sliding form one continuous tetrahedra surface to the other opens a pentagon defined space through the center. Fig.3) Here the same spiral is seen
from another angle with five circles added in the interval spaces between
the tetrahedra. The five circles are all formed to something similar to
a slice of a hexagon pyramid with a center stellated triangle. They are
the same folded units used in fig.12.
Fig.4). Starting with the three diameters,
fold every other point to the center. Leave the triangle folded. Fold each
end point to the mid point on the opposite side of the triangle. Do to
all three diameters one at a time. Do not do one on top of the other. These
nine creased lines form the tetrahedra.
Figure 5 a, b, c: This shows three variations of tetrahedron pattern form changes. Fig.5a) Four 4-frequency folded circles are reformed each into a bi-tetrahedron with one tetrahedron open. The open tetrahedron triangles are joined to form an icosahedron pattern, 12 triangles and 8 open triangle planes. The four circle centers (end points) are the four points of the tetrahedra.. The circumferences are folded to the inside. Fig.5b) This is the same system shown in Fig.5a. with the circumferences folded to the outside. Fig.5c) This is a slight variation to Fig.
5b. The surfaces have been changed by depressing some of the creases.
There are always variations to any given configuration. This is the fun
of exploring and playing with the many different possible combinations.
Figure 6: 120 paper plate circles in a dodecahedron pattern.
Figure 7: 4 paper plates in tetrahedron pattern. Fig.6) There are sixty individual units. Each unit is made by joining two tetrahedra. One is opened to an octahedron pattern. The other is a closed tetrahedron which is placed upside down into the open octahedron pattern. This stabilizes the open octahedron. Five of these open octahedron units are placed into a pentagon ring and glued together. As octahedron units are added to the pentagon it begins to round itself into a dodecahedron pattern of 12 pentagons. The angles are built into the pattern forming of the folds. Nothing is measured or calculated. This sphere has a 21 inch diameter. Fig.7) Each circle is folded in an 8-frequency grid.
Forming the center hexagon they are folded into a truncated slice of a
tetrahedron form with a hexagon on one face and a triangle on the opposite
face. The circumference is folded to the outside and curved rather than
staying with the creased lines. They are all folded the same. The four
triangle faces are to the inside joined on the edges. This forms a tetrahedron
space on the inside and the hexagons are in positions that show a truncated
tetrahedron pattern.
Figure 8: 16 circles in a tetrahedron pattern.
Figure 9: 2 paper plates in an octahedron pattern. Fig.8) Each individual circle is folded and curved into a three-ribbed configuration. Four units are then joined on their curved surfaces into a tetrahedron pattern. The four sets of four are again joined into a tetrahedron pattern, this time they are joined on the ribbed edges keeping the center open. This is an open system where there are no enclosed spaces. A combination of creases and curves are used. Fig. 9) Each circle is folded forming the center hexagon face with circumferences folded out. The circumference is joined in sets of three forming three distinct points. The two circles are joined together on the hexagon faces leaving the six points to form an octahedron pattern.
Figure 10: Stellated octahedron fractal. Fig.10) This is an exercise in fractal growth that started with a stellated octahedron using 9 inch paper plates. It was made by folding only tetrahedra, as shown in fig.4. With each scaling down the diameter of the circle was cut down enable to fold a proportionally correct tetrahedra. I stopped with the 2½ inch diameter circle because my fingers do not fold well beyond that scale. The degree of fractal development towards the inside was simply a decision to show that fractal development occurs not only on boarders but internally as well. This is a way to show various scales of development within the stellated octahedron. The stellated octahedron, also known as a tetrastar, is the primary polyhedral form of a self-referencing fractal pattern.
Figure 11: 7 circles in hexagon helix formation.
Figure 12: 80 circles in icosahedron pattern. Fig.11) The individual unit to make this helix started by forming the regular tetrahedron with all 24 creases shown in fig 1f. The top two thirds were folded onto each other forming the lower third of a sliced tetrahedron form. Each end point of the folded over triangles were move to touch the center point on each edge, one over the other, forming a triangle congruent to the base triangle. This creates a twisting with three open triangle spaces. The direction points are moved to the edge mid points will determine the direction of twist. As with most single formed units there are many possibilities of how to join them in multiples. In this case they all twist in the same direction and are joined by only one of the nine divisions of the three frequency triangle faces. This was done so the extended edge of the open spaces lined up to form one continuous edge to the helix form. Fig.12) Start with the large six-frequency folded triangle. Fold in the three half hexagons at the mid point of each side. This will give form to the center hexagon and create tetrahedron intervals between the three trapezoid shapes. Bring the three end points of the large triangle together and overlap the end triangles. These three triangles can be pushed in to form another inverse tetrahedron interval, left flat overlapping, or extended forming a small tetrahedron on top. The latter is what was done here. Four of these units were joined in a triangle pattern where three are around one that is upside down in the center. There is a partial face overlapping of the trapezoids of the three to the center unit forming a triangular unit of four circles. The angles are such that twenty of these triangle units will join to form an icosahedron spherical pattern that clearly shows the dodecahedron pentagons.
Figure 13: 36 circles in a helix pattern wth two identical interlocking systems. Fig.13) The single circle is folded to the tetrahedron, fig.4. The circle is folded in half on one of the diameters. The center point is pushed in forming an inverted tetrahedron space with a radial edge coming out from the center to an end point. Give a curve to both sides of the circumference and join them together on the curved edges. This forms the single unit that is used to for this particular helix. Each circle is joined to the next on the straight edges so all the straight edges are to the inside and the curve edges to the outside of the helix. A long and a short section were made and the short section was then twisted into the larger section. This spiral segment is 36 circles reformed using only the nine creases that form the tetrahedron. There are other variations to be made with this particular reconfiguration.
Figure 14: 4 sequential variations on the stellated tetrahedron. Fig. 14) Each model is a variation on the stellated tetrahedron.They are made with 4 circles, each folded to the tetrahedron. They are joined edge to edge forming the center tetrahedron space. In the first variation the edges are opened to form curving surfaces and vesica shaped openings. As the end points of the triangles move further out on the edge lines the curved edge rolls in more. This can happen until all the three triangles sides of the stellations are tightly rolled cones on the edges of the center tetrahedron.
Figure 15: 14 circles in cuboctahedron pattern. Fig. 15) There are two different folded units to meke this cuboctahedron pattern. One is triangular, folded to three edges that indicate the right angle cube corner. Six circles folded in four symmetry where the center becomes an inverted half octahedron are placed on the sx sides. This second unit is formed by folding in two sixth of the circle where the six inverted square pyramids form the six points of the octahedron. This view is from the perspective of the octahedron and cube edges crossing.
Figure 16: 71 paper plate. Fig. 16) These circles have been reformed into various frequencies of tetrahedra in different combinations and arrangements. This has been given the form of a personal image rather than a traditional abstract image in geometric form. There is no limit to style or size when folding the circle. Play is an important part of discovering the circle. There is much that is unexpected and surprising in this process of decomposing spherical information. Fig. 17) This is a more of a sculptural piece than the other examples. It is made from folded paper plates all folded to the 3-6 diameter circle. Some have been folded to the 4-frequency in fig.1e, and some of the 8-frequency diameter grid in fig.1f. There are many different combinations of folding and combining to form this piece. The primary pattern is the five fold symmetry and the helical system that is formed by pentacaps that are joined on triangle faces. This helix form is the base for the extensions that move out into an unusual double helix form. You can see the helix formed by the square tubing. The circles have been reformed into the five, four and three fold symmetries by folding in 1/6, 2/6, and the 3/6 of the circle. There is an interesting angle relationship between five octahedra and the pentagon that form the bottom part. Congruent circles make joining many different combinations of shapes and symmetries easy to do. Often with complex pieces that require a lot of time to make, they get two coats of shellac and a couple of coats of gesso. This adds permanency and durability to the paper keeping the white surface. It does lose some of the light quality you get with paper.
Figure 17: 75 paper plate circles. Just a note about joining and attaching circles together. I use mostly paper plates with masking tape and hair pins when exploring the transforming aspects of the circle. It is easy to change and play with different reformations and arrangements as they come up. When I settle in on a model that shows something interesting I often use a PVA glue, an archival white glue, before taping or using hair pins to hold them together. When the glue is dry remove the tape and/or pins. Sometimes holes are punched and string is used to hold parts together where movement between the parts is necessary. I do not limit myself in how circles need to be attached. I am more concerned with the process and the potential of the circle, and use what kind of joining works best for the system being developed. There is so much more to folding the circle than what has been shown in this paper. It is my hope that some readers will find enough interest to exploring on your own. There is much to be discovered and I always find it interesting to see what other people to do when they start folding circles. For readers that would like more information and pictures
of examples please visit my website: www.wholemovement.com
|