|
William C. Hoffman Institute for Topological Psychology 2591 W. Camino Llano Tucson, AZ, USA 85742
Introduction The bilateral symmetry of the human face is known to be a considerable factor in its attraction. In fact, "averaging" the two sides to induce even greater symmetry increases the attraction (Langlois & Roggman, 1990). Even though the two sides of the face are not perfectly symmetric, the near symmetry is undeniably attractive. To attempt to assess the degree of bilateral symmetry in the human face one can separate the face into its two halves, left L and right R, then flip R in a horizontal reflection to make the halves directly comparable, and finally take the symmetric difference of these two sets for comparison. The situation is rather like that depicted in Figure 7.042 of The Fascination of Groups (Budden, 1972: 64), where the symmetric difference of two sets A and B, which are approximately the same, is depicted. When the two reach identity, the symmetric difference ("one or the other but not both") becomes the null set Ø. On the other hand, the greater the symmetric difference, the greater the degree of asymmetry. Now it also happens that the symmetric difference is one of the two universals for the category of sets (Kostrikin & Shafarevich, 1990: Sec. 20), the other universal being the Cartesian product ´ . As indicated above, it is of both a symmetric and an asymmetric nature in that it measures the degree of equality of two sets, one of which may be a transform of the other. The symmetric difference also plays a key role in the homology of sets as the boundary operator ¶ . Given the aesthetic satisfaction
that accrues to facial symmetry and to symmetry in general, one is led
to wonder whether the symmetric difference may perhaps be involved in a
significant way in the general psychology of perception. In a sense this
is close to Jablan’s (2002) modularity in science and
art, Avital’s "mindprints" (Avital, 1999), and to Markovich’s
amodal completion of visual perception (Markovich,
2002), wherein the antinomy, symmetry-asymmetry, plays an important role.
The symmetric difference, by its very nature, measures symmetry versus
asymmetry. However, with respect to aesthetic satisfaction, the situation
seems to depend more on Riegel’s dialectical psychology (Riegel, 1973,
1977,
1978).
Dialectical psychology posits that we go through life continually encountering
and reconciling contradictions, which arise out of the classical Heraclitean
dialectic of change and incompleteness. As Riegel put it, "Thinking is
the process of transforming contradictory experience into momentary stable
structures."
The symmetric difference and the dialectical pair Dialectic is a word of many meanings (Rychlak, 1976) but taken here as number (8) in the article "Dialectic" in the Encyclopedia of Philosophy (Edwards, 1967), namely, as "…the logical development of thought or reality through thesis and antithesis to a synthesis of these opposites." The essence of dialectic thus lies in the apposition of opposites—thesis and antithesis—that through removal of sensed contradictions arrives at a synthesis, at a higher level perhaps. Associated with every figure, there is a ground. Doubt surrounds every belief: "It could be that way, but is it really?" To every appearance, there is the reality—"the thing in itself." Emotion stems from a primitive approach-avoid reaction. Intelligence involves an exploration of alternatives. Dialectical thinking consists of an exploration of contradictory possibilities that results in a cognition that reduces cognitive dissonance. Kahneman and Miller (1986) state that all perceived events are compared to counterfactual alternatives, counterfactual in that they constitute alternative realities to the one experienced. Thus even without the element of ceaseless change—Heraclitus’s "everything flows"—the distinction between an object or concept and what it is not leads inevitably to a dialectic view of the world. Following Hegel’s axiomatization of dialectic, Riegel (1973) laid down the following three "laws" of dialectical psychology:
I. The unity and struggle of opposites
Here these three "laws" will be expressed, in the contexts of both dialectic and dialectical psychology, by the symmetric difference and its complement. Formally the symmetric difference of two sets A and B is defined by A DB = (A Ç ¬ B) È (¬ A ÇB) = (A ÈB) \ (A Ç B) = ¬ A D ¬ B, (1) while its complement, symbolized by ¬, is ¬ (A DB) = (A ÇB) È ¬ (A ÈB) = (A ÇB) È (¬ A Ç ¬ B) = ¬ A DB = A D ¬ B. (2) The pair of relations (1) and (2) will be referred to as the dialectical pair (D, ¬). The relation to dialectic is made plain below. The symmetric difference operation generates a group upon the category of sets. The null set Ø is the identity: A D Ø = A. It is self-inverse: A DA = Ø, and associative and commutative: A D (B DC) = (A DB) DC, and A DB = B DA. The property A DW = ¬ A, where W denotes the universe of discourse, suggests that complementation of the symmetric difference to form the dialectical pair is a natural operation. Clearly, Eq. (1) for the symmetric difference—"one or the other, but not both"— embodies "law" I. Since both Eqs. (1) and (2) are set-theoretic, they are in accord with "law" II, transformation from quantities to qualitative sets. (But according to a theorem of Nikodym (1930), there also exists a means for going back from the sets themselves via a measure on the sets determined by the symmetric difference. Any world view that would lack measures for geometry and probability must be seriously defective.) Ordinarily "law" III is taken to constitute simple negation. A truly new aspect of "law" III, however, is provided by the dialectical pair formulation in that it is not simple negation but rather the complement of the symmetric difference (1), as expressed by Eq. (2), that corresponds to "law" III. This not only permits synthesis in the product term but also relates the sets involved to everything else in the domain of discourse—their context. Consider then the dialectical properties of the dialectical pair. Hegel’s first triad was "being—nothing—becoming." " Being" is positive; it affirms existence of an object or concept C, which is always accompanied by its complement in the universe of discourse W. The symmetric difference of an object with its complement "becomes"—is everything, namely, the universe of discourse. C D ¬ C = (C Ç ¬ ¬ C) È (¬ C Ç ¬ C) = (C ÇC) È (¬ C Ç ¬ C) = C È ¬ C = W. The second element of the triad, "nothing," is negative; it denies what is being affirmed and is deduced directly from "being," as the null set Ø. This is given by the symmetric difference of an object with itself, C DC = (C Ç ¬ C) È (¬ C ÇC) = Ø È Ø = Ø. Passage of "nothing" into "being" is generated by the symmetric difference: (Ø DC) = (Ø Ç ¬ C) È (¬ Ø ÇC) = Ø È (W ÇC) = C If C should happen to be contained within a larger set C', C ÌC', then C ÈC' is the relative complement of C in C'. Thus D acts as differentia in Hegelian dialectic. The counterpart in formal logic of the set relation (1) is (p Ù ~ q) Ú (~ p Ùq). This expression differs from the Sheffer stroke only by lacking a join with the joint denial term ~ p Ù ~ q. Since all of first order logic can be derived from the Sheffer stroke, this relation between logic and this set-theoretic universal is worthy of note. The second expression (2) corresponds to the first order logic expression for equivalence, (p Ùq) Ú ( ~ p Ù ~q), thus providing a basis for qualia. The dialectical pair thus provides a basis for logical thought as well as the more natural intuition involved in dialectical psychology and psychological categorization. Before proceeding to
the role of the dialectical pair in dialectical psychology, we note parenthetically
that Hegel himself would no doubt have found such formal modeling of dialectic
as that above an abomination. Styazhkin (1969: 112)
comments in connection with Hegel’s denunciation of Ploucquet’s "logical
calculus" that "One can only imagine what epithets Hegel would have
bestowed on contemporary mathematical logic!" Yet Ploucquet’s calculus
for generating a complete set of all logical relations out of only an identity
function and an inconsistency function seems rather close to Hegel’s
own ideas on thesis-antithesis and synthesis.
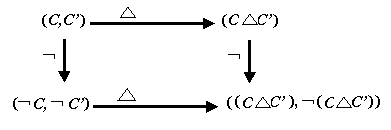
The Dialectical Pair and Dialectical Psychology The "similarities and differences" paradigm is an old story in psychology. Clearly classification depends upon detecting differences, which may then be used to separate objects and concepts into categories of exemplars determined by their closeness to the prototypes. Survival is more dependent upon recognizing novel elements of the environment and classifying them than contemplating their meaning and significance. The commonality of two such stimuli, C Ç C', corresponds to convergent thinking. "Everything else," embodied in the ¬ (C ÈC' ) term in Eq. (2), represents divergent thinking. The dialectical pair, Eqs. (1) and (2), thus encompasses both the "similarities-differences" paradigm and convergent and divergent thinking. As Riegel (1973: 351) put it, Rational thinking (in distinction from reason) separates different attributes and then, by connecting them in a systematic manner, tries to reconstruct the phenomena … in an unequivocal manner… . Dialectical thinking comprehends itself, the world, and each concrete object in its multitude of of contradictory relations. Let us now flesh out the process described in the opening paragraph for determining the degree of bilateral symmetry in a human face. Denote by R' the result of flipping the right half R of the face horizontally. Then the symmetric difference L DR' describes by its nearness to the null set Ø the degree of closeness in appearance. However, the second half of the dialectical pair brings in more aspects of cognitive processing. The complement ¬ (L DR ') = (L ÇR ' ) È ¬ (L ÇR ') not only describes this closeness by the commonality expressed in the first term on the right but also refers the result to the context—not-(L and/or R' )—in the current universe of discourse. The latter will ordinarily include more than shape, bringing in memory, both cognitive and emotional and mental sets that predispose to certain features that are found attractive. Proverbially, "The eyes are the windows of the soul." Such facial features as this that occur within the symmetric pattern also enter into attractiveness. Furthermore, "beauty is in the eye of the beholder." The particular cognitions and emotions within one’s psyche which impart personal aesthetic satisfaction thus factor in also. I have shown elsewhere (Hoffman, 1995, 1997, 1999) that the cognitive factors of categorization, memory (both long-term and working), language, decisionmaking, learning, problem solving, intelligence, and creativity are structured by the dialectical pair. Both psychological categories and mathematical categories stem from equivalence (Mervis & Rosch, 1981; Eilenberg & MacLane, 1945) if emphasis is shifted in the case of psychological categories to functions and away from objects and their attributes. Psychological categories consist of objects with particular attributes structured by prototypes and exemplars that are distinguished from near-neighbor categories by gradients. The system strongly resembles the idea of suspension in topology (Hatcher, 2002). A suspension consists of a double cone joined at the base, with the vertices consisting of the two different prototypes. A mathematical category consists of a collection of objects together with, for each pair thereof, a collection of morphisms, which are arrows mapping objects to one another in an associative way. Mathematical categories also have their objects but the emphasis is placed upon the morphisms which generate the structural diagrams of the category, as in the following commutative diagram in Figure 1for the dialectical pair:
"Chasing around the diagram" is fundamental in category theory and algebraic topology. It is apparently reflected in the mind’s "trains of thought" as chasing around the cognitive diagrams involved in "brain circuits." Memory represents the store of information derived from experience. It is described as sensory, short-term, long-term, working, declarative versus procedural, semantic versus episodic, explicit (conscious) versus implicit (subconscious), etc. Semantic memory is modeled in terms of networks whose vertices are "chunks" and arrows are directed "schema," and so have the geometric nature of a simplicial triangulation of a space or a simplicial complex. A simplicial complex consists of a finite set of simplices which form linear combinations called chains, the boundaries of which are generated by the action of the boundary operator ¶ acting upon the chains. The standard models for memory processing (Chang, 1986) consist of networks which imply that long-term memory L has the character of an ordered simplicial complex. As such, L must contain subcomplexes Lj which correspond to particular memories, semantic or episodic, in L. The set of all such subcomplexes constitutes the power set of L. Suppose v denotes a memory vertex-chunk in some Lj. The star of v, St(v), is defined as the interiors of all those simplices that contain v. The connection with the dialectical pair is immediate: [Lj DSt(v), ¬ (Lj DSt(v))] = [Lj \ St(v), St(v) È (L \ Lj)]. The first term is the complement in Lj . If it is the null set, recall is perfect. Otherwise the second factor acts to have St(v) scan within long-term memory outside of Lj, i.e., to search memory further. Conscious working memory W consists of the conscious boundary of long-term memory L in combination with short-term memory S: W = ¶LÇS. It interacts with the concepts in the working memory from the previous moment and the percepts forwarded via short-term memory from the sensory buffer. Working memory is path-connected. Each path corresponds to a different constituent of the working memory field, thus offering a basis for the decision making among alternatives that constitutes the cognitive executive function. This continuous flow from one working memory to the next thus provides the "flashing stream" (Dodwell, 2001) of consciousness. Intelligence refers to
the mental ability to reason, comprehend complicated concepts, think abstractly,
"transfer" (that is, generalize from experience), and arrive at sound decisions.
Whatever intelligence may connote, it is intimately related to working
memory W (Eysenck, 1967, Wickelgren,
1997). The close connection has also been established by neuroimaging (Gabrieli,
1998). She comments, "Reasoning seems to be the sum of working-memory abilities".
Intelligence acts to strip away confusion, to be "a quick study," and arrive
at the heart of the matter within the context at hand. This of course is
of the nature of the dialectical pair, whose first component strips away
the overlap of concepts and whose second component penetrates quickly to
the commonality and exploration of alternatives that characterizes intelligence.
The first phase of the dialectical pair, Eq. (1), acts to diminish any
confusing common attributes. All that remains after the application CDC'
is the separate character of each with no overlap—no "confusion." Here
the cognitive dissonance generated by the first stage is resolved by whatever
C
and C' may have in common in company with their context in memory
and working memory.
Emotion And Dialectic Presented with an ostensibly aesthetic object, one reacts with either like or dislike, for all the world like the approach-avoidance reaction fundamental to emotion. Human emotion has evolved over long eons out of the basic approach-avoidance reaction found at the level of the reptilian brain. This "survival brain" within the primitive midbrain has added higher centers during the course of evolution: the limbic system, or "emotional brain," and the coldly calculating neocortex, which acts as a brake upon basic reactions. Emotions separate into two major groups, the unpleasant ones of anxiety, disgust, hate, and anger in one, and the pleasant emotions—joy, pride, hope, and affection—in the other. This bipolar nature of emotion lends itself nicely to the dialectical pair. Emotion E distinguishes itself from emotion E' via E DE ', while at the same time ¬ (E DE ' ) permits one to love and hate at the same time. The bipolar scale between approach and avoid is termed emotional valence. The accompanying emotional intensity scale is called the activation level. The stronger the activation and valence, the more an emotion is likely to be felt as a "pure" emotion. Emotion emerges as a
more less surprising change from a core of calmness that corresponds to
Campos
and Caplovitz’s (1988) normative "invariant core of affective continuity."
As Ellsworth (1994) puts it, "The possibility of a
valenced response—‘this event may be good or bad for me’—is enough to elicit
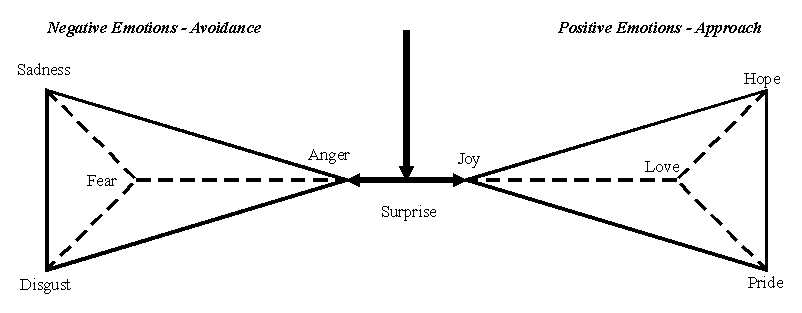
emotion." The situation is depicted in the symmetric tetrahedral patterns
of Figure 2.
Calm Awareness
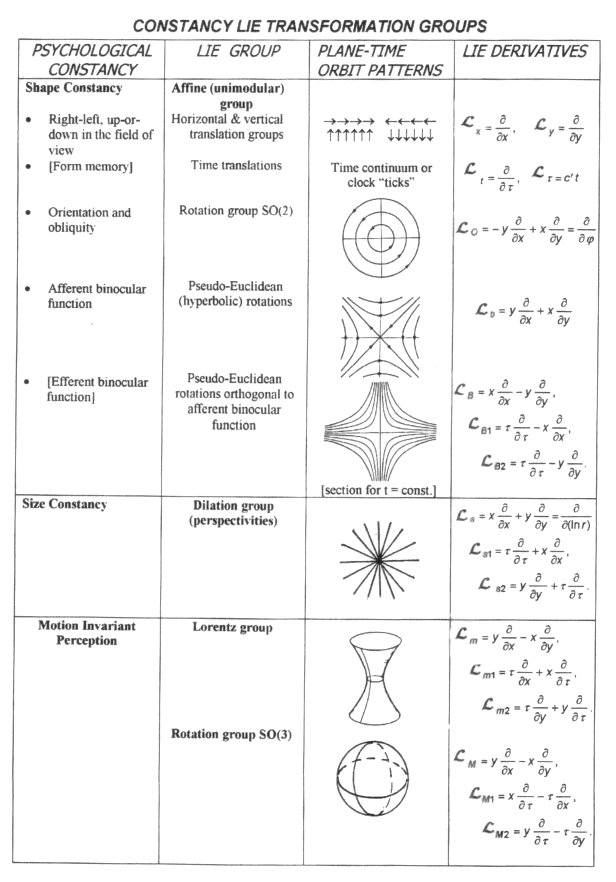
Figure 2. Paired tetrahedral representation of the generation of bipolar emotions by surprise out of a "core of calmness." An aesthetically satisfying object is not just an object. It has form and meaning. We have dealt with the cognitive aspect above. Here we examine the psychological basis for aesthetic form and claim that the well known relation in physical science: invariance Þ symmetry Þ conservation law carries over here to where the invariances are those of the psychological constancies. Psychological conservation resides in the continuous symmetry of the constancies and form memory. Psychological constancy in the visual case refers to the invariant recognition of perceived objects no matter what distortion may be imposed on them by viewing conditions: location in the field of view, rotation, binocular perception, apparent size, state of motion (as long as they are not "moving too fast for the eye to follow"), and color. Pitch and loudness constancies and binaural perception constitute similar invariances for audition. The visual constancies, their associated continuous transformation groups, Lie derivatives, and local orbit structures are listed in Table I (Hoffman, 1966a, 1978, 1984). Recall that invariance under a continuous (Lie) transformation group means annulment of the invariant by the Lie derivative and that the local orbit structure is determined by means of the associated Pfaffian system.
Good design is thought to reside not so much in the realization of form but in the elimination of "misfit" (Alexander, 1967). That is, there is a subconscious response to forms that are found naturally in the perceptual system, like the constancy orbit patterns. "Love at first sight" involves immediate strong recognition of some subconscious ideal pattern. Certain basic structures in the neuropsychology of form perception are known to embody the patterns of the psychological constancies (Van Essen and Gallant, 1994). Ornamentation, primitive as well as modern, exhibits many of these basic patterns. Optical Art also involves these basic patterns (Hoffman, 1966b), and the Golden Ratio postulated to govern the aesthetic properties of facial and body dimensions ( www.goldennumber.net) also makes its appearance as the logarithmic spiral generated by the combined action of size constancy (the dilation group in log r ) and the rotation component of shape constancy, with rotation angle j .
According to (Pronzato, Wynn, and Zhigljavskii, 2000). this Golden-Ratio combination serves for optimal search of the visual field. See Huntley (1990) for a full discussion of the wide role of the equiangular spiral in nature and beauty. I suggest that this harmony among the Golden Ratio, the aesthetically satisfying spirals that are found throughout nature, and the psychological constancies constitutes the psychological basis for the pleasurable perceptions imparted by the Golden Ratio. Gary Meisner’s website www.beautyanalysis.com shows a collection of images depicting the role of the Golden Ratio in nature, the human body, and the human face and supports a strong claim that Phi , the Golden Ratio, is the key to beauty. Michael Semprevivo (http://goldennumber.net/color.htm) has developed a software called PhiBar to express in terms of the Golden Ratio the color spectrum relationships that produce rich, appealing color combinations. But when one considers the stages that art has gone through from shamanic cave art thousands of years ago to abstract expressionism of today, it is clear that fashion and learning impose considerable influences upon such intrinsic psychological systems as the constancies and Gestalt "laws." There is often a conflict between the art appreciation of one generation and the next. When "les Fauves" first burst upon the scene in Paris in 1905, the art critics and the public were decidedly negative. Yet this furor over non-traditional use of contour and color gradually subsided and in time was replaced by appreciation for the impressionist school (though an educated taste might still be required). Cognitive and emotional influences are as much involved in art appreciation as perceptual ones, perhaps even more so. The emotional impact of an art object or style may well be negative at first sight but after enough learned meanings have been assimilated and associated with the structural elements consonant with the basic perceptual symmetries an appreciation of the art form develops, if indeed the latter possesses any aesthetic import at all. Given the progressive interactions during this learning process among emotion E, long-term memory L, and aesthetic satisfaction A, the triple symmetric difference relation (E DL) Ç (LDA) Ç (A DE) = Ø (see Appendix) represents by its annulment the commonality of acceptance. But any theory that purports
to offer a psychological basis for art appreciation must account for such
abstract expressionist paintings as those of Jackson Pollock. These action
paintings, uncharitably attributed to "Jack the dripper," consist of lines,
curves, and colors that derive from the painter’s wrist motions and dancing
about while flinging paint. The elements of the human psyche that respond
to such formless patterns must be very basic indeed, even more so than
for cave art and Paleolithic ornamental art. If so, it must involve invariances
and so symmetries that are very fundamental indeed to the human condition,
something like Gibson’s "formless invariants." The writer (Hoffman, 2001)
has suggested that the fundamental geometric element of curvature is one
such, and here I offer the suggestion that Heraclitus’s panta rhei—everything
flows—is another. A flow represents the local orbit structure of a Lie
transformation group, perceived here as the vigorous flow of color and
form responding to psychological constancy independent of cognitive recognition.
The presence of the constancies in the human perceptual system is what
accounts for abstract expressionism.
Appendix: Table of Symmetric Difference Relations
References Alexander, Christopher. Notes on the Synthesis of Form. Harvard University Press, Cambridge, Massachusetts (1967). Avital, Tsion, Mindprints: The structural shadows of mind-reality, Visual Mathematics 1(2) (1999). Budden, F. J., The Fascination of Groups, Cambridge University Press, Cambridge, UK, (1972). Campos, J. J. and B. Caplovitz, A new understanding of emotions and their development. In Emotions, Cognition, and Behavior, Izard, C. E., J. Kagan, and R. B. Zajonc (Eds.), Cambridge University Press, New York (1988). Chang, T. M., Semantic memory: Facts and models, Psychological Bulletin 99 (1986) 199-220. Daniell, P. J., The modular differences of classes, Bulletin of the American Mathematical Society 23 (1916-1917) 446-450. Dodwell, P. C. Brave New Mind, Oxford University Press, New York (2001). Edwards, E. (Ed.), Encyclopedia of Philosophy, Macmillan, New York (1967). Eilenberg, S. and MacLane, S. General theory of natural equivalences, Transactions of the American Mathematical Society 58 (1945) 231-294. Ellsworth, P. C., Some reasons to expect universal antecedents of emotions. In The Nature of Emotion: Fundamental Questions, Ekman, P. and R. J. Davidson (Eds.). Oxford University Press, New York (1994). Eysenck, H. J, Intelligence assessment: A theoretical and experimental approach, British Journal of Educational Psychology 37 (1967) 81-98. Gabrieli, J. D., Cognitive neuroscience of human memory, Annual Review of Psychology 49 (1998) 87-115. Annual Reviews,Inc., Palo Alto, California. Hatcher, Allen, Algebraic Topology, Cambridge University Press, New York (2002). Hoffman, William C., The Lie algebra of visual perception, Journal of Mathematical Psychology 3 (1966a) 65-98. Hoffman, William C., Comments on optical art, 5 (1966b) 873-874. Hoffman, William C., The Lie transformation group approach to visual neuropsychology. In Formal Theories of Visual Perception, Leeuwenberg, E.L.J. and H. Buffart (Eds.), pp. 27-66, John Wiley, Chichester, UK, (1978). Hoffman, William C., Figural synthesis by vectorfields. In Figural Synthesis, Dodwell, P. C. and T. Caelli (Eds.), Erlbaum Associates, Hillsdale, NJ, (1984). Hoffman, William C., The dialectics of giftedness: Gifted intellect and creativity, Roeper Review 17 (1995) 201-206. Hoffman, William C., Mind and the Geometry of Systems. In Two Sciences of Mind: Readings in Cognitive Science and Consciousness, O’Nualla’in, S., P. McKevitt, and E. Mac Aogain (Eds.), pp. 459-483, John Benjamins, Amsterdam, (1997). Hoffman, William C., Dialectic—a universal for consciousness? New Ideas in Psychology 17 (1999) 251-269, (1999). Hoffman, William C., Group theory and geometric psychology, Behavioral and Brain Sciences 24 (2001) 674-676. Huntley, H. E., The Divine Proportion: A Study in Mathematical Beauty, Dover Publications, New York, (1970). Jablan, Slavik, Modularity in art and science, Visual Mathematics 4 (1) (2002) #10. Kahneman, Daniel and D. T. Miller, Norm theory: Comparing reality to the alternatives, Psychological Review 93 (1986) 136-153. Kostrikin, A. I. and I. E. Shafarevich, (Eds.), Algebra I: Basic Notions of Algebra, Encyclopedia of Mathematical Sciences, Springer-Verlag, Berlin, (1990). Langlois, J. H. and Roggman, I. A., Attractive faces are only average, Psychological Science 1 (1990) 115-121. Markovich, Slobodan, Amodal completion in visual perception, Visual Mathematics 4 (1) (2002) # 15. Mervis, C. B. and E. Rosch, Categorization of natural objects, Annual Review of Psychology 32, pp. 89-115, Annual Reviews, Inc., Palo Alto, California, (1981). Nikodym, Otto, Sur une generalization des integrale de M. J. Radon, Fundamenta Mathematica 15(1930) 131-179. Pronzato, Luc, Wynn, Henry P., and Zhigljavskii, Anatoly A., Dynamical Search: Applications of Dynamical Systems in Search and Optimization, CRC, Boca Raton, Florida, pp. 15-16, 134-141, and 203-204, (2000). Riegel, Klaus F., Dialectic operations: The final period of cognitive development, Human Development 16 (1973) 346-370. Riegel, Klaus F., The dialectics of time. In Life-Span Developmental Psychology: Dialectical Perspectives in Experimental Research, Datan, N. and H. W. Reese (Eds.), pp. 3-45, Academic Press, New York, (1977). Riegel, Klaus F., Psychology mon amour, Houghton-Mifflin, Boston, (1978). Rychlak, Joseph F., The multiple meanings of ‘dialectic’. In Humanistic Rationale for Behavior and Development, Rychlak, J. F. (Ed.), S. Karger, Basel, (1976). Styazhkin, N. I., A History of Mathematical Logic from Leibniz to Peano, MIT Press, Cambridge, Massachusets, (1969). Van Essen, David C. and Jack L., Neural mechanisms of form and motion processing in the primate visual system, Neuron 13 (1994) 1-10. Wickelgren, I., Getting a grasp
on working memory, Science 275 (1997) 1580-1582.
|