Symmetry analysis of rhythmic structure

 

We will illustrate the proposed procedure with the example of a hypothetic rhythmic structure (Fig. 2.5).

Figure 2.5 A hypothetic rhythmic structure prepared for a symmetry analysis.

After assigning a corresponding numerical value T(S)_k to each measure, the most important part of the task is the interpretation of the results. In the case of the studied rhythmic structure we may draw the following conclusions:

1. The distribution of numerical values T(S): within the studied rhythmic structure made up of sixteen measures, the numerical value of 6 appears four times, the value of 20 appears once, the value of 18 appears three times, the value of 24 six times and the value of 48 two times. The measures which correspond to equal numerical values T(S) are permutationally equal, i.e., they share the same rhythmic content.

2. The distribution of codes T(S)_k: the code 61 corresponds to the 1st, 15th and 16th measure, which points to translational repetition. For T(S)=6, the possible values of the lower index k are 1 and 2 (as [1/2] and [1/4] can give only two possible arrangements). The code 6₂ corresponds to the 14th measure which points to retrograde repetition. In the case where T(S)=18 the possible values of the lower index k are 1, 2 and 3 (as [1/2], [1/4] and [1/4] can only give three different permutations with repetition). This means that within the studied rhythmic structure all symmetry possibilities for T(S)=18 have been used, in a cyclic order (18₁, 18₂, 18₃). The codes 18₁ and 18₃ which correspond to the 2nd and 8th measure point to retrograde repetition. In the case of T(S)=24 there are six possible permutations with the repetition of elements [1/4], [1/4], [1/8], [1/8] and all have been used. The pairs of codes 24₁ and 24₆ which correspond to the 5th and 11th measures and 24₂ and 24₅ which correspond to the 7th and 9th measure point to the existence of retrograde repetition. Because of the strictly periodical order of these codings (24₃, 24₁, 24₂, 24₅, 24₆, 24₄) which correspond to the 3rd, 5th, 7th, 9th , 11th and 13th measure, retrograde repetition represents not only local, but also global symmetry in the substructure level. Finally, in the case of measures coded as 48₄ (the 6th measure) and 48₂₇ (12th measure), retrograde repetition is found.

3. The relationships between the numerical values T(S): the sum of values T(S) which correspond to the 1st and 2nd measure (6+18=24), when multiplied by 2, gives 48. When we examine the order of note durations we can conclude that the 6th measure can be obtained by applying the method of diminishment, and that the 12th measure is obtained by applying retrograde diminishment on the first two measures. The sum of the values T(S) which correspond to the 14th and 15th measure (6+6=12), when multiplied by 2 gives 24. If we study the order of the note durations we may conclude that these two measures can be obtained by applying the method of retrograde augmentation in the 3rd measure, and of augmentation on the 13th measure. The same is true of the 15th and 16th measure. They can be derived by augmentation from the 7th measure, and by retrograde augmentation from the 9th measure. In terms of the half-phrases, it is possible to see permutational repetition in half-phrases 5-6, 11-12, and 12-13, and in half-phrases 2-3, 3-4, 4-5, 7-8, 8-9, 9-10, 10-11. The same is true of 3-4-5, 7-8-9 and for 5-6-7 and 11-12-13.

Finally, a more versatile application of permutational proportionality is possible. We can apply different proportional augmentations or diminishments with the aim of obtaining a new rhythmic entity. For example, from rhythmic entity S₁=(¹/₂,¹/₄) (to which diminishment has been applied) and rhythmic entities S₂=(¹/₂, ¹/₈, ¹/₂) and S₃=(¹/₄, ¹/₄, ¹/₈, ¹/₈) (to which double diminishment has been applied) we obtain a new rhythmic entity S=(¹/₄, ¹/₈, ¹/₈, [1/16],[1/16], [1/32], [1/32], [1/32], [1/32]), and so forth. Although it does not pose major problems, a detailed analysis of such procedures has been omitted because of its extensiveness and a great number of possibilities.

By applying this method it is possible to analyze the symmetry of a rhythmic structure of real musical pieces (Fig. 2.6)

Figure 2.6 The Art of the Fugue by J.S. Bach, an example of diminishment (Skovran and Pericic, 1986).

The study of the symmetry of a rhythmic structure within polyphonic musical pieces is reduced to the study of the composition of linear symmetric structures. Without straying away from a general approach, we can illustrate this problem with an example of a two-part composition, In this case, besides the already mentioned symmetry relationships that exist between rhythmic structures within every linear component (higher or lower voice), it is also necessary to examine the symmetry transformations which translate the rhythmic entities of one component to the rhythmic entities of a second component. In this case, the following transformations of correlation may occur:

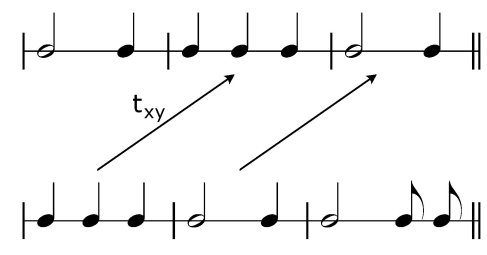
1. translation on the y-axis t_y (Fig. 2.7 a);

2. translation on the x and y-axes t_x,y (Fig. 2.7 b)

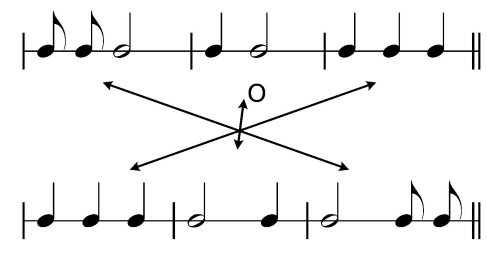
3. central reflection O (Fig. 2.7 c)

(a)

(b)

(c)

Figure 2.7 Symmetry transformations of a two-part rhythmic structure: a) t_y; b) t_x,y; c) O.

The following group of transformations of polyphonic musical pieces is made up of transformations of proportionality. Each one of them can be presented as an action of one of the mentioned isometric transformations followed by a proportional augmentation or diminution of all note durations that belong to the studied rhythmic entity. Besides that, it is possible to study also the permutational congruence or permutational proportionality of rhythmic entities that belong to linear components (voices). By defining the transformations that connect the linear components it is possible to conduct a precise analysis of the different aspects of complementary rhythms and polyrhythms which appear in polyphonic compositions (Lemacher and Schroeder 1967, p. 21-22).