|
Relative symmetry transformations of melodic structure
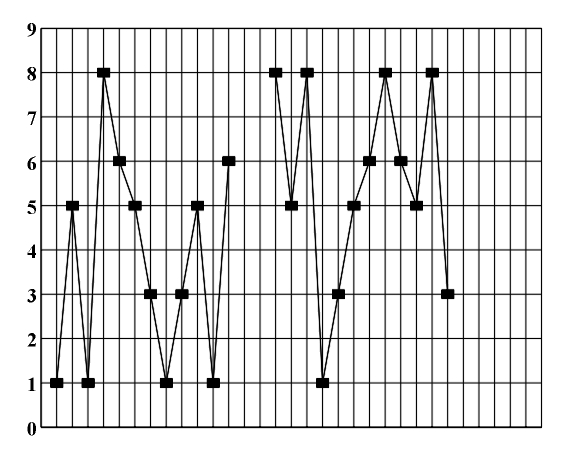
In nature, and especially in art, ideal symmetry occurs very rarely. This is why in music similarity symmetry, i.e., relative symmetry transformations, prevail. For example, instead of absolute (strict) inversion, free inversion usually occurs (Fig. 3.22). For every relative transformation we can determine its exact statistic parameters, which show the degree of its deviation from the absolute transformation of the same name:
For example, in the case of free inversion (Fig. 3.22) the absolute deviation ||i1|-|i1'||+...+||in|-|in'|| equals 6, while the relative deviation [(||i1|-|i1'||+...+||in|-|in'||)/n]=[6/11] ~ 0.545..., where intervals of the initial structure have been denoted, respectively, as i1,...,in, and intervals of inverted structure have been denoted as i1',..., in'.
Figure 3.22 J.S. Bach, Fugue W.KL.II, F-sharp major - an example of free inversion (Skovran and Pericic, 1986). Polyphonic pieces may be analyzed from the aspect of symmetry of their melodic structure as a superposition of unison melodic contents. In the following chapters Symmetry of Counterpoint and Symmetry of Harmony we will deal with the symmetry analysis of polyphonic pieces in more detail.
|