|
Symmetry of interval and seventh-chord structure of scales
In continuation we will endeavor to analyze the interval and chord structure of scales and their corresponding tonalities from the theory of symmetry point of view, as a basis for the symmetry analysis of harmony. In the preceding chapter we defined the concept of same-name intervals and, based on it, we introduced the concept of the minimal same-name interval. The origin of all natural scales is the periodic tone sequence ...0,2,4,5,7,9,11,12... where the period is 12. Individual scales (modes) are acquired by choosing an initial point. We will attempt to present a symmetry-based argumentation for the reasons of singling out a natural major and a natural minor scale, as basic scales. Beginning with point 0, by reducing all the intervals of tone sequence ...0,2,4,5,7,9,11,12... to minimal sam-name intervals, we get a table showing the interval structure of all possible scales (modes):
Thanks to symmetry, this table can be reduced to a diagonal table:
If we denote the interval values 6,5,4,3,2,1 with a full or broken lines so that the thickness of the line shows a descending sequence, the result is a circular symmetric diagram (Fig. 5.1). Two significant properties become visible immediately:
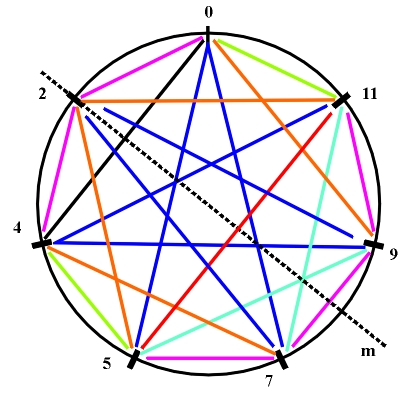
Figure 5.1 A diagram of the interval structure of a tone sequence ...0,2,4,5,7,9,11,12... after reduction to minimal same-name intervals. Because of the instability of the tritone, points 2,5,11 are not suitable to be the initial points of a scale. Among the remaining potential candidates, points 0,4 and 9,7 make up two pairs of mirror-symmetric (equivalent) points. This means that the remaining possible non-equivalent initial points of the scales are 0 and 9. Depending on whether we choose the first or the second one, our results are non-equivalent sequences 0,2,4,5,7,9,11,12 or 9,11,12,14,16,17,19,21 (i.e., 0,2,3,5,7,8,10,12). These sequences represent a natural major and minor sequence, the seven degrees of the natural major and minor scale (Fig. 5.2). (a)
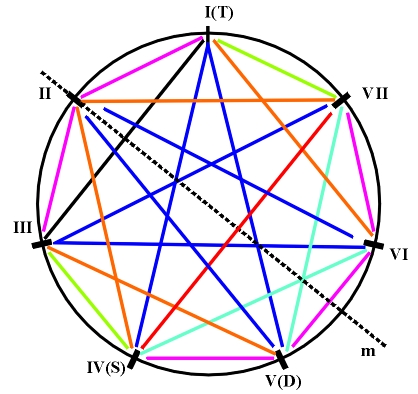
(b) Figure 5.2 A diagram of the interval structure of the natural major (a) and minor (b). After assigning appropriate numeration to the degrees, we can directly read their chord structure from the diagrams of symmetry of interval structure. By reading the appropriate fifth-chords we get a table of their distribution in the natural major and minor:
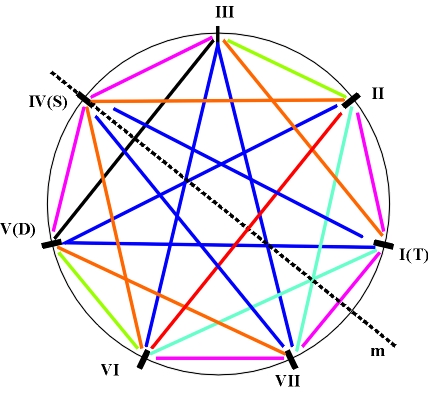
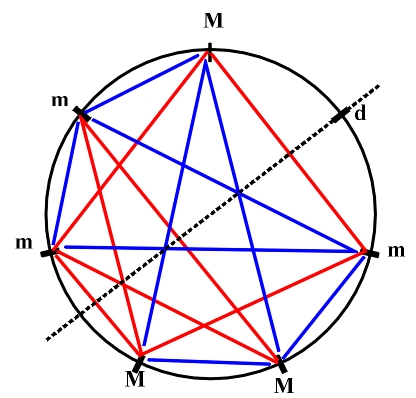
If we denote the symmetry relations 1 which link the fifth chords that belong to the same tonal mode with full lines, and use thinner lines for antisymmetric relations 2 which link fifth chords that belong to opposite tonal modes, as a result we get symmetry diagrams of the fifth-chord structure. We can directly note the triangles of the principal harmonic functions I, IV, V (T,S,D), as well as the axis of antireflection which contains the VII degree in the major, or the II degree in the minor key (the center of instability) (Fig. 5.3).
Figure 5.3 The axis of antisymmetry which contains the VII degree in the major, and the II degree in the minor key. For every two fifth-chords we can determine a common number of tones, i.e., their coefficient of similarity. It can have a value of 0,1 or 2. The similarity of chords will be the main criterion for determining secondary harmonic functions t, s, d, which occur in the II, III, VI, and VII degree. This means that the secondary harmonic function of a given degree is determined based on the maximum of similarity of the fifth-chord on the studied degree with the tonic, subdominant and dominant five-chord. The complete table of the principal and secondary harmonic functions is as follows:
For all secondary functions, the coefficient of similarity with the same-name principal functions is 2. We can note that two secondary functions each correspond with the III and VI degree. In order to opt correctly for one of them in each individual case, we must first determine the direction of the harmonic crescendo - a sequence of principal harmonic functions, classified according to ascending instability. At first sight, the presence of the axis of symmetry in the diagram of symmetry of interval structure (Fig. 5.3) leads us to assume the absence of enantiomorphism (the appearance of the left and right orientation in the major and minor tonalities), i.e., to assume its non-orientability. However, we draw an opposite conclusion based on the fifth-chord structure. In the major key, the center of instability (tritone) is found on the VII degree, whose secondary function is dominant (d). Thus, we are dealing with a d-tritone, since its corresponding fifth-chord is closer in similarity to the dominant fifth-chord (coefficient of similarity 2), than to the subdominant (coefficient of similarity 1). 1"Static" according to D. Despic (1987) 2"Kinetic" according to D. Despic (1987)
|