|
Repetitive symmetry
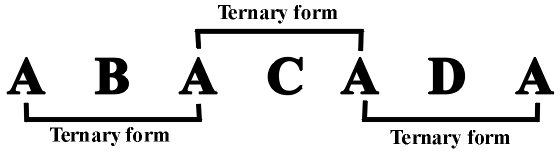
Repetitive (translational) symmetry occurs within different musical forms based on the principle of repetition or imitation. Besides the forms based on simple repetition (e.g., binary form), there are forms based on combinations of repetitions (refrains) and variations - songs with a refrain (a-b-c-b-d-b-e-b-f-b), or a rondo with several themes (A-B-A-C-A-D-A-F...+coda). These forms can be considered as examples of antisymmetric translation (repetition), and also as conjoining of ternary mirror-symmetric forms (Fig. 7.6). Simple or multiple periodicity occurs as a type of translational symmetry (these are so-called "periodic groups" according to L. Mazel and V. Zuckerman: the appearance of periodicity pairs a-a-b-b within the first two quarter measures of the third movement of the Symphony no. 1 by G. Mahler (Fig. 7.7), or the periodicity pairs from Konchak's aria in the Prince Igor opera by A. Borodin) (Fig. 7.8). Translational repetition often occurs with continued forms, such as Six Ecossaises for piano by L. van Beethoven which are unified by episode (A) which plays the role of a refrain (Fig. 7.9), or in the non-standard rondo form Waltz in A flat major, op. 42 by F. Chopin (B-A-C-A-D-A-E-A-B-A-D-A).
Figure 7.7 (Mazel and Zuckerman, 1967) Especially interesting are the repetitive forms based on the principle of gradual progression, "chain link" between the neighboring parts, where each of them announces the next one (according to the formula ab+bc+cd+...). This principle was used in S. Prokofiev's Sonata no. 9 where at the end of each part the basic theme of the next part is announced, and in the final coda the main theme of the first Alegretto occurs again. In this manner, a closed-cycle composition is obtained, similar to a sonnet sequence in poetry (Sokolov, 1974. p. 60). In the same way it is possible to register repetitional symmetry in the tonal plane in a musical piece.
Figure 7.8 (Mazel and Zuckerman, 1967).
|