|
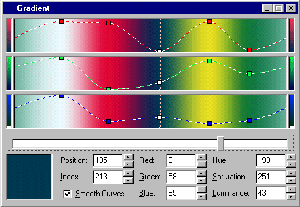
Coloring Algorithms Every dynamical system produces a sequence of values z0, z1, z2… zn. Fractal images are created by producing one of these sequences for each pixel in the image; the coloring algorithm is what interprets this sequence to produce a final color. Typically, the coloring algorithm produces a single value for each pixel. Since color is a three-dimensional space, this one-dimensional value must be expanded to produce a color image. The common method is to create a palette, a sequence of 3D color values; these are connected end-to-end and the coloring algorithm value is then used as a position along this multi-segmented line (the gradient). If the last palette color is connected to the first, a closed, segmented loop is formed and any real value from the coloring algorithm can be mapped to a defined color in the gradient. This is similar to the pseudo-color renderings often used for infra-red imaging. Gradients are normally linearly interpolated in RGB space (Red, Green, Blue), but they can also be interpolated in HSL space (Hue, Saturation, Lightness) and interpolated with spline curves instead of straight line segments. The selection of the gradient is one of the most critical artistic choices in creating a good fractal image. Color selection can emphasize one part of a fractal image while de-emphasizing others. In extreme cases, two images with the same fractal parameters, but different color schemes will appear totally different. Some coloring algorithms produce discrete values, while some produce continuous values. Discrete values will produce visible stepping when used as a gradient position; until recently this was not terribly important, as the restriction of 8-bit color displays introduced an element of color stepping in gradients anyway, and discrete coloring values were mapped to corresponding discrete color in the gradient. With the introduction of inexpensive 24-bit displays, algorithms which produce continuous values are becoming more important, as this permits interpolating along the color gradient to any color precision desired. With the increasing significance of coloring algorithms it is surprising that there has been no attempt to classify the variety of algorithms that are popping up. The following sections of this paper may be considered as an initial classification system for the most important algorithms.
Fig 1. Gradient window linearly interpolated in RGB space with spline curves.
VisMath Home |