|
by Jay Kappraff New Jersey Institute of Technology Newark NJ kappraff@aol.com
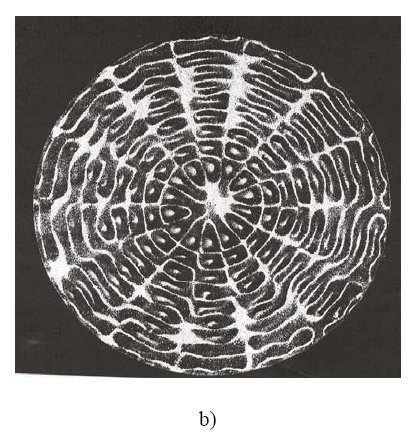
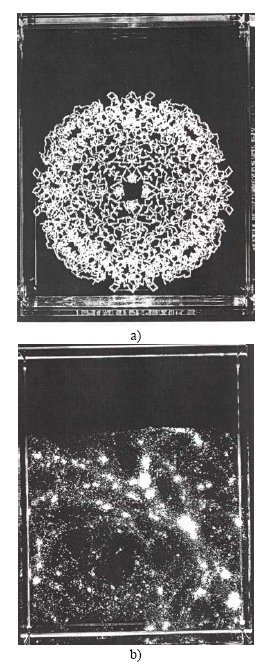
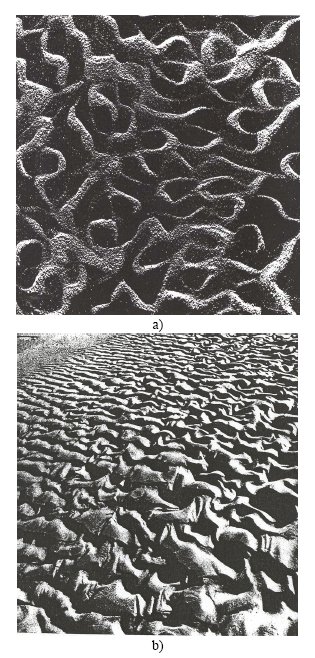
Kauffman and Varela propose the following experiment: Sprinkle sand or place a thin layer of glycerine over the surface of a metal plate; draw a violin bow carefully along the plate boundary. The sand particles or glycerine will toss about in a rapid dance, swarming and forming a characteristic pattern on the plate surface. This pattern is at once both form and process: individual grains of sand or swirls of glycerine play continually in and out, while the general shape is maintained dynamically in response to the bowing vibration. Hans Jenny in his book Cymatics [1] has noted from this experiment: "Since the various aspects of these phenomena are due to vibration, we are confronted with a spectrum which reveals patterned figurate formations at one pole and kinetic-dynamic processes at the other, the whole being generated and sustained by its essential periodicity. These aspects, however, are not separate entities but are derived from the vibrational phenomenon in which they appear in their unitariness." These are poetic ideas, metaphoric
notions, and yet they have reflections in all fields from the wave/particle
duality of quantum physics, to oscillations within the nervous system to
the oscillations and distinctions that we make at every moment of our lives.
Complexity and self-organization emerge from disorder the result of a simple
process. This process also gives rise to exquisite patterns shown in Figure
1.
Figure 1: a) Pattern formed by the vibration of sand on a metal plate; b) Vibration of a thin film of glycerine. From Cymatics by Hans Jenny.
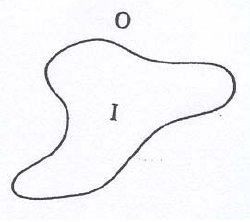
G. Spencer Brown in his book Laws of Form [2] has created a symbolic language that expresses these ideas and is sensitive to them. Kauffman [3] has extended Spencer-Brown’s language to exhibit how a rich world of periodicities, waveforms and interference phenomena is inherent in the simple act of distinction, the making of a mark on a sheet of paper so as to distinguish between self and non-self or in and out(see Figure 2). There is nothing new about this idea since our number system with all of its complexity is in fact derived from the empty set. We conceptualize the empty set by framing nothing and then throwing away the frame. The frame is the mark of distinction.
Figure 2: A mark of distinction separating inside from outside.
I have found that number
when viewed properly reveals self-organization in the natural world from
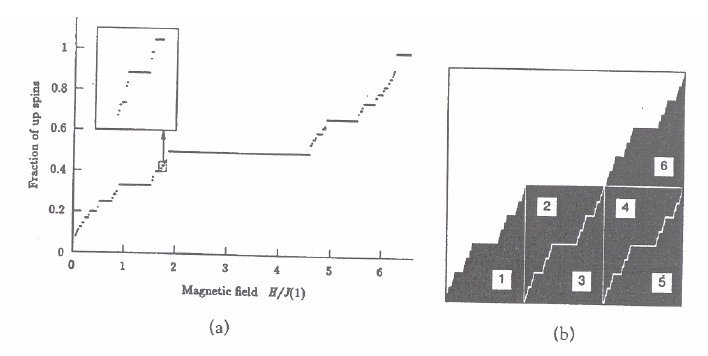
subatomic to cosmic scales. The so-called "devil’s staircase" shown in
Figure 3 places number in the proper framework and reveals a hierarchy
of rational numbers in which rationals with smaller denominators have wider
plateaus and lead to more stable resonances. The devil’s staircase is a
representation of the limiting row of the Farey sequence the first eight
rows of which is shown in Figure 4. The n-th row is simply a list of all
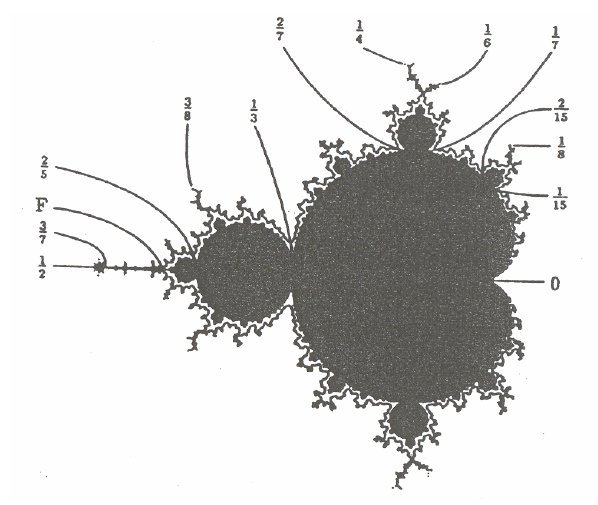
rational fractions with denominators n or less. Notice that row 8 on the
interval from 0 to ½ contains all of the critical points on the
Mandelbrot set, important for describing chaos theory, where the rationals
are fractions of a circle when the Mandelbrot set is mapped from a circle
(see Figure 5). On the other hand the interval from ½ to 1 contains
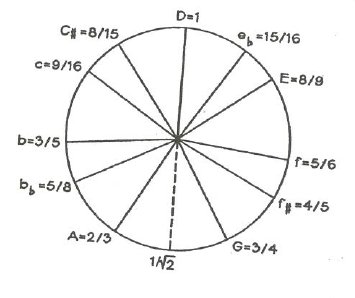
many of the tones of the Just musical scale shown on the tone circle in
Figure 6, including the tritone (5/7) and the diminished musical seventh
(4/7) used in the music of Brahms. Only missing are the dissonant intervals
of the semitone and the wholetone [4].
Figure
3: a) The devil’s staircase exhibited in the Ising model from Physics;
b) The devil’s staircase subdivided into six self-similar parts.
Figure
4: The first eight rows of the Farey sequence.
Figure
5: The Mandelbrot set showing critical values of the external angles at
fractions from row eight of the Farey Sequence.
Figutre 6: The Just scale shown on a tone circle. Note the symmetry of rising (clockwise) and falling (counterclockwise) scales. In Figure 7 the number of
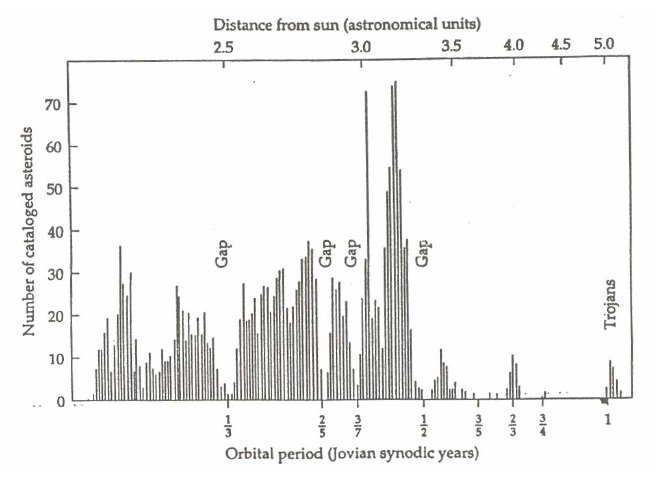
asteroids in the asteroid belt is plotted against distance from the sun
in units of Jupiter’s orbital period Notice that sequence of gaps in the
belt are at the rational numbers: 1/3, 2/5, 3/7, ½, 3/5, 2/3, ¾
and that these are consecutive entries to rows 6 and 7 in the Farey sequence.
I have found (not shown here) that this same Farey sequence also expresses
the hierarchy of phyllotaxis numbers that dictate the growth of plants
from pinecones to sunflowers [4].
Figure 7: Number of asteroids plotted against distance from the sun (in units of Jupiter’s orbital period). Gaps occur at successive points in the Farey sequence. From Newton’s Clock by I. Peterson Copyright ã 1992 by I. Peterson. We see here that without a telescope or without a living bud or the sound of a musical instrument, our very number system already contains the objects of our observations of the natural world and is capable of reproducing phenomena in all of its complexity. How did this come to pass. Are we observing an objective reality or are we projecting our own organs of perception onto the world? These are deep questions for philosophical study. From the earliest times humans have tried to make sense of their observations of the natural world even though they often experienced the world as chaotic. Their very existence depended on reliable predictions of such events as the arrival of spring to plant, fall to harvest, the coming and going of the tides, etc. The movement of the heavenly bodies provided the first experiences of regularity in the universe and the application of number to describe these motions may have constituted the earliest development of mathematics. In ancient times astronomy and music were tied together. The earliest cultures were aural by nature and music played an important role as confirmed by the many musical instruments found in burial sites of ancient Sumerians from the third and fourth millennia B.C. There is evidence that the Sumerians were aware of the twelve tone musical scale in which tones were represented by the ratio of integers or rational numbers placed on a tone circle with 12 sectors similar to the positions of the planets in the zodiac [5]. In the East the pentatonic scale of five tones chosen from the twelve was prevalent corresponding to the five observed planets. In the West seven tones was the norm since the sun and moon were added to the planets. Expressing the musical scale
in terms of rational numbers has certain problems associated with it. It
was well understood that a bowed length of string has a higher pitch when
it is shortened. For example, if a string representing the fundamental
tone is divided in half it gives an identically sounding pitch referred
to as an octave. Also the inverse of the string length gives the relative
frequency, so that the octave has a frequency twice the fundamental. The
key interval of the musical scale is the musical fifth gotten by taking
a length of string whose tone represents the fundamental tone say D and
reducing it to 2/3 or its length. A succession of twelve musical fifths
placed into a single octave gives rise to the twelve tone chromatic scale
known as "spiral fifths" as shown in Figure 8. Its serpent like appearance
leads the ethnomusicologist, Ernest McClain to suggest that this scale
lies at the basis of the many serpent myths in all cultures.
Figure 8: Serpent power: the spiral tuning of fifths. Courtesy of Ernest McClain.
On a piano which is tuned so that each of the intervals of the 12 tone scale are equal in a logarithmic sense (the equal-tempered scale), beginning on any tone and playing twelve successive musical fifths, results in the same tone seven octaves higher. Referring to Figure 8, the first and thirteenth tones in spiral fifths, Aflat and Gsharp, the tritone or three wholetones located at 6 o’clock on the tone circle, are the same tone in different octaves. However, in terms of rational fifths they differ by about a quarter of a semitone, the so-called Pythagorean comma. This is true because in order for (2/3)12 to equal (1/2)7 it would follow that 312 = 219 which is certainly false. Unless a limit is placed on the frequency of the tones, the use of rational numbers to represent tone would require an infinite number of tones. This presented ancient civilizations with a kind of 3rd millennium B.C. chaos theory. Similar problems faced early
astronomers as they sought to reconcile the incommensurability of the cycles
of the sun and the moon. The solar cycle of 365 ¼ days does not
mesh with the lunar cycle of 354 days. A canonical year of 360 days was
chosen as a compromise between the two. It turns out that the ratios 365
¼ : 360 and 360:354 are both approximately equal to the Pythagorean
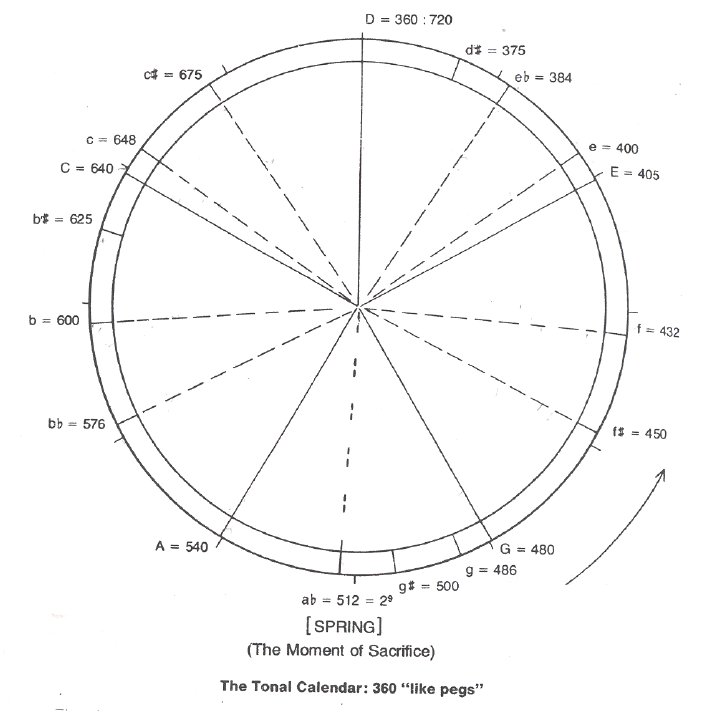
comma so that the musical scale had some roots in astronomy. Also if an
octave is limited by relative frequencies of 360 to 720 eleven of the tones
of the Just scale can be placed as integers within this limit missing only
the tritone which you can verify by comparing the intervals of the following
sequence with Figure 6 and 9 (the rational numbers represent relative string
lengths):
Figure 9: The Just scale shown as integers on a tone circle. Note the symmetry.
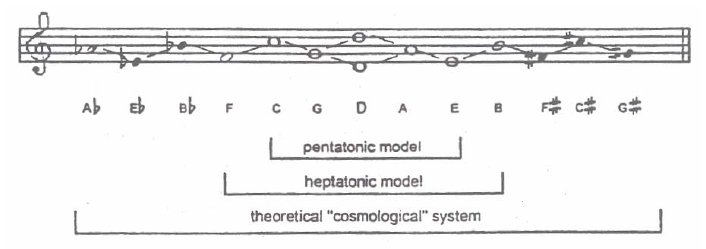
All ancient scales were expressed in terms of integers with the integers of the Just scale divisible by primes 2,3, and 5 while the scale of "spiral fifths" were expressed by integers divisible by primes 2, and 3. Notice in Figures 6 and 9 that the tones of the Just scale are placed symmetrically around the tone circle. This is the result of symmetrically placed rational fractions in Sequence 1 being inverses of each other when factors of 2 are cancelled, e.g., 5/6 º 5/3 as compared with 3/5. But factors of 2 result in the same tone in a different octave. Compare the limit of 360/720 with the limit of 286,624/573,268 required for spiral fifths. So the Just scale embodies the two great lessons of the ancient world, the importance of balance and limit in all things. Ernest McClain has traced the use of music as metaphor in the Rig Veda, the works of Plato and the Bible in his books and articles [6],[7],[8]. To ancient mathematicians
and philosophers, the concept of rational number was thought to lie at
the basis of cosmology, music, and human affairs. On the other hand, while
the concept of an irrational number was not clear in the minds of ancient
mathematicians, it was understood that rational numbers could be made to
approximate certain ideal elements at dividing points of the tone circle
into 12 equal sectors, what is now known as the equal tempered scale with The part of the continuum which lies beyond rational number belongs to non-being (Asat) and the Dragon (Vtra). Without the concept of an irrational number, the model for Existence (Sat) is Indra. The continuum of the circle (Vtra) embraces all possible differentiations (Indra). The conflict between Indra and Vtra can never end; it is the conflict between the field of rational numbers and the continuum of real numbers..
This battle between rational and irrational numbers continues into the present where it lies at the basis of chaos theory and the study of dynamical systems. In chaos theory no rational approximation to an irrational number is good enough in terms of yielding closely identical results as I shall demonstrate. Three decades ago scientists began to realize that many of the phenomenon that they thought to be deterministic or predictable from a set of equations were in fact unpredictable. Changing the initial conditions by as small an amount conceivable led to entirely different results. For example, a rational approximation to an irrational initial condition, no matter how good the approximation, would lead eventually to totally different results. The system of equations predicting weather was one such set of equations. In fact as soon as the equations were more complicated than linear, built into them was chaotic behavior. In other words the fluttering of a butterfly’s wings in Brazil could, in principle, over time affect the weather patterns in New York. The growth of plants is another
natural system that appears to exist in a state of incipient chaos [4].
Notice that when the cells of a plant are placed around the stem successively
at angles, known as divergence angles, related to the golden mean of 2p
/f radians the spiral forms reminiscent of sunflowers appear. Change the
divergence angle to a close rational approximation of the golden mean and
the spiral is lost and replaced by a spider web appearance (see Figure
10).
Figure
10: a) A computer generated model of plant phyllotaxis with rational divergence
angle 2p x13/21. Note the spider web appearance;
Consider the simple map governing the Mandlebrot set [9], z --> z2 + c for z and c complex numbers. Beginning with an initial
point z0 and replacing this in the map leads to the trajectory
z0,
z1,z2,
z3, … The Mandelbrot set constitutes all values of c
that lead to bounded trajectories. This sensitive dependence on initial
conditions holds for values of c outside of the Mandelbrot set. If the
value of c is taken internally and away from the boundary of the Mandelbrot
set the behavior of the trajectory is simple, leading either to a fixed
point or a periodic orbit. The Julia set is the boundary of the set of
points of the trajectory that do not escape to infinity. For example, when
c = 0, the Julia set is a unit circle. Points outside the Mandelbrot set
lead to chaotic behavior of the kind just mentioned. Points near the boundary
of the set have the most interesting behavior. One such Julia set for a
point near the boundary of the Mandelbrot set is shown in Figure 11. This
is somewhat like the state of affairs that exists at the shoreline between
land and ocean. The frozen character of the land as opposed to the chaotic
nature of the ocean is mediated by the tide pools at the interface between
the two. This is where life has its greatest diversity. Stuart Kauffman
referred to this region of great differentiation as the "edge of chaos"
[10].
Figure 11: A "dragon" shaped Julia set for a value of c at the boundary of the Mandelbrot set.
There is a strong relationship between chaos and fractals. In fact Julia sets generally have a fractal nature. The study of fractals had its beginning with the research of Benoit Mandelbrot into the nature of stock market fluctuations. However, such structures were noticed earlier by Lewis Richardson in his study of the length of coastlines. Richardson noticed that there was a power law relating the apparent length of coastlines when viewed at different scales. When viewed at a large scale such as the scale of a map, the coastline appears finite. But if the scale is reduced so that all of the idiosycracies of the coastline are evident, the ins and outs of the coastline have no apparent limit and its length is effectively infinite. Furthermore, a small stretch of coastline is similar to the whole when viewed in a statistical sense. Robert Cogan and Pozzi Escot have shown that music also has a fractal nature [11]. For example they show that musical structures appear and reappear throughout the musical score at different scales. This is the consequence of the music also satisfying a power law referred to as 1/f noise found in the structure of the music of Bach and Mozart [12]. 1/f noise has a spectrum of sound between the spectrum of Brownian motion in which the next note is completely determined from the previous notes resulting in a frozen quality in the music, and white noise in which the tones are randomly chosen leading to a chaotic sound. So we see that good music is again the result of finding the "edge of chaos." Good art also strives to
incorporate the elements of self-similarity although this is generally
done subtly. In a great work of art each image must related to the others
in terms of its geometry and metaphorical themes. Artists and sculptors
have always been inspired by the complex forms of nature. For example the
vortices in Van Gogh’s famous painting, "Starry Night" in figure 12a appears
to be taken directly from the meandering stream winding through separate
vortices in Figure 12b. Trains of vortices also appear in the knarled cypress
trees found in many of Van Gogh’s late paintings such as "St Paul’s Hospital,
(1889)" of Figure 13a and perfectly embody the bark and knots of the cypress
tree in Figure 13b. On the other hand, the design on a palm leaf from New
Guinea represent yet another set of vortices shown in Figure 14a and b.
Figures 12b, 13b, and 14b were taken from the beautiful photos of complexity
in nature found in Theodor Schwenk’s book, Sensitive Chaos [14].
Figure
12: a) Van Gogh’s painting, "Starry Night". About this painting Van Gogh
wrote, "First of all the twinkling stars vibrated, but remained motionless
in space. Then all celestial globes united into one series of movements…Firmaments
and planets both disappeared, but the mighty breath which gives life to
al things and in which all is bound up remain [13].";
b) a meandering stream winding through separate vortices. From Sensitive
Chaos by Schwenk [14].
Figure
13: Van Gogh’s painting, "St. Paul’s Hospital, (1889)". Van Gogh wrote,
" The cypress are always occupying my thoughts---it astonishes me that
they have not been done as I see them."; b) The bark and knots of a cypress
tree from Schwenk [12].
Figure 14: a) Design on a palm leaf (May River, New Guinea) Volkerkundliches Museum, Basel; b) A vortex train from Schwenk [14].
Manuel Baez (see this issue)
creates sculptures reminiscent of complex forms from nature out of bamboo
sticks and rubber band connectors [15] resulting in
structures whose whole is greater than the sum of its parts. Baez describes
his system as follows: "These dynamic processes are inherently composed
of interweaving elemental relationships that evolve into integrative systems
with startling form and structure generating capabilities". Beginning with
a simple shape such as a square or pentagon, a module is created which
is replicated over and over. Since the sticks are flexible, the model inter-transforms
into amazing shapes illustrating the order which exists within apparent
chaos. Three structures from his "Phenomenological Garden" all made with
12" and 6" bamboo dowels and rubber bands are shown in Figure 15. They
were all generated from a simple square pattern.
Figure 15: The Phenomenological Garden of Manuel Baez. Bathsheba Grossman invites
scientists and mathematicians to send her complex images from their work
such as proteins or globular clusters from astronomy or complex geometrical
forms and recreates them as three dimensional sculptures in a variety of
medias. Her "Cosmological Simulation" (see Figure 16a) was created from
simulated scientific data and illustrates the fractal nature of the universe.
"Ferritin Protein" (see Figure 16b) is a three-dimensional model in laser
etched crystal made from a protein data bank file. Her bronze sculpture
"Metatron" is shown in Figure 17. It is made by a lost wax process and
created from an operation upon a cube and an octahedron. It appears to
be as a singular vortex fixed in time and is evocative to me of frozen
music.
Figure
16: a) Large scale model of a cosmological simulation; b) Ferritin, a symmetrical
protein;.Courtesy of Bathsheba Grossman.
Figure 17: The Metatron. Courtesy of Bathsheba Grossman.
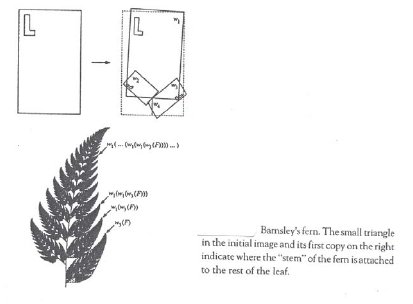
Barnsley [16]
has shown that fractal images can be created by subjecting an initial seed
figure to the following transformations: contractions, translations, rotations,
and affine transformations (transformations that transform rectangles to
arbitrary parallelograms). For example, Barnsley’s fern is created by repeatedly
transforming an initial rectangle to three rectangles of different sizes,
proportions, and orientations and one line segment as shown in Figure 18.
This approach to generating fractals is leading to revolutionary ways of
understanding how complex structures arise from simple ones, and it is
being applied to many applications from image processing to generation
of fractal scenes for movie sets such as that shown in Figure 19 generated
by Kenneth Musgrave.
Figure
18: Barnsley’s fern. Created by repeated transformation from a rectangular
seed pattern.
Figure 19: A fractal scene by Kenneth Musgrave.
Structures and designs with
fractal properties appear quite naturally in many cultures. I will present
two examples from Ron Eglash’s book African Fractals [17].
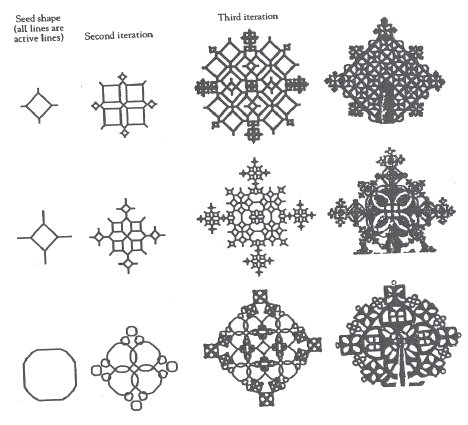
In the western part of the Cameroons lies the fertile grasslands region
of the Bamileke. Eglash describes their fractal settlement architecture
(see Figure 20).
Figure
20: a) Fractal simulation of Bamileke architecture. In the first iteration
("seed shape") the two active lines are shown in gray.
"These houses and the attached enclosures are built from bamboo—Patterns of agricultural production underlie the scaling. Since the same bamboo mesh construction is used for houses, house enclosures, and enclosures of enclosures, the result is a self-similar architecture—The farming activities require alot of movement between enclosures, so at all scales we see good-sized openings."
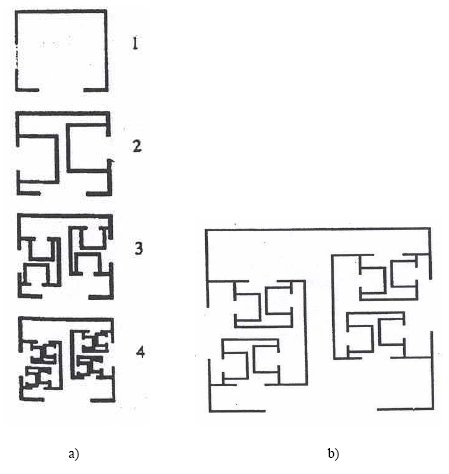
Many of the processional
crosses of Ethiopia indicate a threefold fractal iteration (see Figure
21). Eglash suggests that the reason that the iteration stops at three
may be for practical reasons. Two iterations is too few to get the concept
of iteration across, while more than three presents fabrication difficulties
to the artisans.
Figure 21: Fractal simulation for Ethiopian processional crosses through three iterations. From African Fractals by Ron Eglash [15].
The twentieth century was a revolutionary time in the history of mathematics and science. First the deterministic nature of physics was replaced by the strange world of quantum mechanics where the outcomes of an experiment depended on probability counter to the intuition of Albert Einstein that "God does not play dice." Then the foundations of mathematics were shaken by Kurt Godel who showed that a mathematical system could not be both consistent and complete while Alan Turing discovered that there was no way of determining whether a computer program would halt once given some initial data. Mathematical and scientific theories are created by observing symmetries of all sorts. This enables the information inherent in the physical system to be compressed into a theory or set of equations. For example, all of the possible motions of celestial or earthbound bodies are governed by Newtons laws which is elegantly stated as F = ma. Knowing only a few facts about the initial motion, in other words only a few bits of information, the theory can predict the ensuing motion. What if the system exhibited no such symmetry? Then each specific instance would have to be observed in its entirety. In other words, no information would have been compressed for us to unlock by a theory. All we could do would be to observe each orbit and record what we saw. Systems generated by rules in which the next state is determined by the flipping of a coin is an example of a system devoid of symmetry. There is no way to determine the final state of the system except by following the coin flips to their conclusion. Similarly in mathematics, a mathematical system is generally compressed by stating several axioms representing a finite number of bits of information from which an unlimited number of theorems follow. Without axioms mathematics would not be concerned with judging truth or falsity but rather with generating patterns. G.J. Chaitin [18]
has recently shown that rather than being an irrelevant curiosity, this
state of affairs, reflected in Godel’s and Turing’s discoveries, is central
to the representation of nature by mathematics and science. He created
a number from number theory with the property that the determination of
its digits was equivalent to flipping coins. We can now say that, it may
be that only narrow islands of observation may be derivable from our standard
equations and theories. As a result mathematicians have begun to realize
that other approaches would be needed to characterize natural phenomena
and to coax information from nature. One such program is being explored
by Stephen Wolfram in his book A New Kind of Science [19].
Figure 22: a) An example of a system defined by the following rule: at each step, take the number obtained at that step and write its base 2 digits in reverse order, then add the resulting number to the original one. Dark squares represent 1 while light squares 0. For many possible starting numbers, the behavior obtained is very simple. This picture shows what happens when one starts with the number 16. After 180 steps, it turns out that all that survives are a few objects that one can view as localized structures. From A New Science by S. Wolfram [19]; b) A network of veins of sand created by the interplay of sand and water. From Schwenk [14].
Wolfram studied the behavior
of a large class of systems governed by rules in which the next state of
the system was determined by the previous state, so-called cellular automata.
In response to simple rules and starting with simple initial conditions,
complex forms would emerge such as the one in Figure 22a. Compare this
with one of the network of veins of sand created by the interplay of sand
and water shown in Figure 22b by Schwenk. Wolfram discovered that all such
automata could be classified as being one four types and that naturally
occurring systems of growth from plants and animals to blood vessels to
crystals, some of which are shown in Figure 23, were themselves cellular
automata exhibiting the same properties as the artificial ones he created.
Furthermore he discovered an astounding principal which he refers to as
the Principal of Computational Equivalence which states that all processes,
whether they are produced by human effort or occur spontaneously in nature,
can be viewed as computations. Furthermore, in many kinds of systems particular
rules can be found that achieve universality, in other words, the ability
to function as a computer in all of its generality, e.g., a universal Turing
machine. The dramatic discovery of his book was to show that rather than
being a rare event, such universality could be created out of simple rules.
Figure 23: A collection of patterns from nature suggesting natural cellular automata. From A New Science by S. Wolfram. This new approach to science
is an invitation for artists and scientists to draw closer to one another.
After all, the examples of ornamental art have patterns similar to ones
generated by cellular automata. For example, Figure 24 illustrates several
eamples generated by cellular automoata reminiscent of the Ethiopian designs
of Figure 20. Hans Jenny’s and Theodor Schwenk’s vibratory patterns offer
another link between art, science and nature. Figure 25a from Jenny [1]
shows particles of sand in a state of flow being excited by crystal oscillations
on a steel plate. Compare this with Figure 25b from Schwenk [14]
showing the ripple marks in sand at a beach.
Figure
24: Cellular automata generated by simple rules with the appearance of
Ethiopian crosses. From A New Science by S. Wolfram [19].
Figure 25: a) Particles of sand in a state of flow excited by crystal oscillations. From Jenny [1]; b) Ripple marks of sand on a beach. From Schwenk [14].
We are heading into an exciting
new era of scientific and mathematical explorations in which artists, musicians
and scientists will be joining hands to help each other and the rest of
us to understand our universe in all of its complexity. More and more the
question will be asked: Is it art or is it science? Mathematics will serve
as the common language, scientists and engineers will create the technology,
and artists and musicians will provide the spirit. These new approaches
will suit our age and society much as ancient systems of thought met the
needs of those cultures. Just as ancient systems of numerology were incorporated
into the myths, religious symbolism and philosophy of those ages, the new
science of complexity and chaos theory is certain to spawn its myths and
metaphors for our age.
Bibliography 1. Jenny, H., Cymatics, Basel: Basilius Press (1967). 2. Spencer-Brown, G. I, Laws of Form, London:George Allen and Unwin, Ltd. (1969). 3. Kauffman, L.H. and Varela, F.J., "Form Dynamics," J. Soc. And Bio. Struct.3 pp161-206 (1980). 4. Kappraff, J. Beyond Measure: A Guided Tour through Nature, Myth, and Number, Singapore: World Scientific (2003). 5. McClain, E.G., "Musical theory and Cosmology", The World and I (Feb. 1994). 6. McClain, E.G., Myth of Invariance, York Beach, Me.:Nicolas-Hays (1976,1984) 7. McClain, E.G., The Pythagorean Plato, York Beach, Me.:Nicolas-Hays (1978,1984). 8. McClain, E.G. "A priestly View of Bible arithmetic in philosophy of science, Van Gogh’s Eyes, and God: Hermeneutic essays in honor of Patrick A. Heelan", ed. B.E. Babich, Boston: Kluwer Academic Publ. (2001). 9. Peitgens, H-O., Jurgens, H., and Saupe, D., Chaos and Fractals, New York: Springer (1992). 10. Kauffman, S.A., The Origins of Order: Self Organization and Selection and Complexity, New York: Oxford Press (1995). 11. Cogan, R. and Escot, P., Sonic Design: The Nature of Sound and Music, Englewood Cliffs, NJ: Prentice Hall (1976). 12. Gardner, M., "White and brown music, fractal curves and one-over-f fluctuations," Sci. Am., v238, No.4 (1978). 13. Purce, J., The Mystic Spiral, New York: Thames and Hudson (1974). 14. Schwenk, T., Sensitive Chaos, New York: Schocken Books (1976). 15. Baez,
M.A., The Phenomenological Garden, In On Growth and Form: The
Engineering of Nature, ACSA east Central Regional Conference, University
of
16. Barnsley, M., Fractals Everywhere, San Diego: Academic Press (1988). 17. Eglash, R., African Fractals, New Brunswick: Rutgers Univ. Press (1999). 18. Chaitin, G.J. "A century of controversy over the foundations of Mathematics," Complexity, vol. 5, No. 5, pp.12-21, (May/June 2000). 19. Wolfram, S. A New Kind of Science, Champaign, IL: Wolfram Media, Inc. (2002).
|