: The Josephus Problem in : Recursive relations and some
![]()
![]()
![]()
:
The Josephus Problem
in : Recursive
relations and some
There
is a very interesting fact about the function
![]() .
.
Example
3.1 The list of the sequence
![]() is
is
![]()
We denote this sequence
![]() modulo 2 by
modulo 2 by
![]() .
Then
.
Then
![]() is
is ![]()
We can find a very beautiful pattern if we arrange them as the
following.
|
|
(3.1) |
|
|
(3.2) |
We
are going to present a formula for this pattern in Theorem 3.2.
Lemma
3.1 (a)
![]() is odd number for any non-negative integer
is odd number for any non-negative integer
![]() .
.
(b)
![]() is even if and only if
is even if and only if
![]() for any natural number
for any natural number
![]() .
.
Proof
(a) By
(2),(4),(6) and (8) of Theorem 2.1
we know that
![]() is odd number for any odd number
is odd number for any odd number
![]() .
.
(b-1) Suppose that
![]() for some natural number n. If
for some natural number n. If
![]() is even, then By (1) of Theorem 2.1
is even, then By (1) of Theorem 2.1
![]() =1,
=1,
which implies that
![]() .
Then by (1) of Theorem 2.1
.
Then by (1) of Theorem 2.1
![]() Conversely if
Conversely if
![]() ,
then by (1) of Theorem 2.1
we have
,
then by (1) of Theorem 2.1
we have
![]() .
Then
.
Then
![]() =1 and by (1) of Theorem 2.1
we know that
=1 and by (1) of Theorem 2.1
we know that
![]() is even. We have proved (b) for
is even. We have proved (b) for
![]() .
.
(b-2) Suppose that
![]() for some natural number n. By the same method that we used in (b-1)
we can prove that
for some natural number n. By the same method that we used in (b-1)
we can prove that
![]() is even if and only if
is even if and only if
![]() .
Similarly we have
.
Similarly we have
![]() if and only if
if and only if
![]() .
.
(b-3) Suppose that
![]() for some natural number n. By the same method that we used in (b-1)
we can prove that
for some natural number n. By the same method that we used in (b-1)
we can prove that
![]() is even if and only if
is even if and only if
![]() .
Similarly we can prove that
.
Similarly we can prove that ![]() if and only if
if and only if
![]() .
.
(b-4) Suppose that
![]() for some natural number n. By the same method that we used in (b-1)
we can prove that
for some natural number n. By the same method that we used in (b-1)
we can prove that
![]() is even if and only if
is even if and only if
![]() .
Similarly we can prove that
.
Similarly we can prove that ![]() if and only if
if and only if
![]()
Our
aim in this section is to prove the existence of the pattern in
![]() .
By Lemma 3.1
.
By Lemma 3.1
![]() is even if and only if
is even if and only if
![]() ,
and hence it is important to know
,
and hence it is important to know
![]() or not for any natural number
or not for any natural number
![]() .
.
Lemma
3.2
![]() Suppose that
Suppose that
![]() or
or
![]() ,
then
,
then
(a)
![]() or
or
![]() ,
,
(b)
![]() or
or
![]() ,
,
(c)
![]() or
or
![]() and
and
(d)
![]() or
or
![]() respectively.
respectively. ![]() Suppose that
Suppose that
![]() or
or
![]() ,
then
,
then
(e)
![]() or
or
![]() ,
,
(f)
![]() or
or
![]() ,
,
(g)
![]() or
or
![]() and
and
(h)
![]() or
or
![]() respectively.
respectively.
Proof
![]() (a) First we suppose that
(a) First we suppose that
|
|
(3.3) |
By
(1) of Theorem 2.1
![]() ,
and hence by
,
and hence by
![]()
|
|
(3.4) |
By
![]() and
and
![]() we have
we have
![]() .
.
Next we suppose that
|
|
(3.5) |
By
Theorem 2.1 and
![]()
|
|
(3.6) |
By
![]() and
and
![]() we have
we have
![]() .
.
Therefore we have proved (a) of this theorem.
By the similar
method we are going to prove (b), (c) and (d).
Suppose that
![]() or
or
![]() .
Then by Lemma 2.1
.
Then by Lemma 2.1
![]() ,
and hence we have
,
and hence we have
![]() or
or
![]() .
.
(b) By (2) of Theorem 2.1
we have
![]() or
or
![]() respectively. Therefore we have proved (b).
respectively. Therefore we have proved (b).
(c) By (3) of Theorem
2.1 we have
![]() or
or
![]() respectively.
respectively.
We have proved (c).
(d) By (4) of Theorem 2.1
we have ![]() or
or
![]() respectively. We have proved (d).
respectively. We have proved (d). ![]() Next we are going to prove (e),(f),(g) and (h). Suppose that
Next we are going to prove (e),(f),(g) and (h). Suppose that
![]() or
or
![]() .
.
(e) By (5) of Theorem 2.1
we have
![]() or
or
![]() respectively.
respectively.
We have proved (e).
(f) By (6) of Theorem 2.1
we have
![]() or
or
![]() respectively.
respectively.
We have proved (f).
(g) By (7) of Theorem 2.1
we have
![]() or
or
![]() respectively.
respectively.
We have proved (g).
(h) By (8) of Theorem 2.1
we have
![]() or
or
![]() respectively.
respectively.
We have proved (h).
Definition
3.1 To use
Lemma 3.2 we need a function. We define
![]() by
by
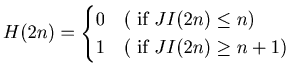
for
any natural number
![]() and
and 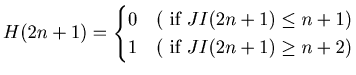
for any non-negative integer
![]() .
.
In
short
![]() = 0 or 1 if
= 0 or 1 if
![]() is in the first or the second half of the list
is in the first or the second half of the list
![]() .
.
![]() is a useful function when we study the pattern in
is a useful function when we study the pattern in
![]() .
.
Lemma
3.3 Let
![]() be a natural number. (1)
be a natural number. (1)
![]()
![]() .
(2)
.
(2)
![]()
![]() if and only if
if and only if
![]()
Proof This is direct from Definition 3.1 and Lemma 3.1.
This
function
![]() has simple recursive relations.
has simple recursive relations.
Lemma
3.4 Suppose that
![]() or
or
![]() ,
then
,
then
(1)
![]() or
or
![]() ,
,
(2)
![]() or 0,
or 0,
(3)
![]() or
or
![]() and
and
(4)
![]() or
or
![]() respectively.
respectively.
Suppose that
![]() or
or
![]() ,
then
,
then
(5)
![]() or 0,
or 0,
(6)
![]() or
or
![]() ,
,
(7)
![]() or 0 and
or 0 and
(8)
![]() or
or
![]() respectively.
respectively.
Proof This is direct from Theorem 3.2 and Definition 3.1.
Example 3.2 The sequence {H(n), n = 1,2,... } has a very beautiful pattern. First we make a triangle with H(n) for n = 1,2,3,..,31.
|
|
(3.7) |
We
are going to calculate each H(n) using Definition 3.1
and Lemma 3.4.
Since JI(1)=1, JI(2)=1,
JI(3) = 3, by Definition 3.1 we have
H(1) = 0, H(2) = 0, H(3) = 1.
Since H(1) = 0, let n = 0 and by
using (5), (6), (7) and (8) of Lemma 3.4 we
have {H(4), H(5), H(6), H(7)} = {1,0,1,0}.
Since H(2) = 0 and
H(3) = 1, let n = 1 and by using (1), ..., (8) of Lemma 3.4
we have
{H(8),H(9),H(10),H(11),H(12),H(13),H(14),H(15)} =
{0,1,0,1,0,1,0,1}.
Since H(4) = 1 and H(5) = 0, let n = 2 and by
using (1), ..., (8) of Lemma 3.4 we have
{H(16),H(17),H(18),H(19),H(20),H(21),H(22),H(23)} =
{1,0,1,0,1,0,1,0}. Since H(6) = 1 and H(7) = 0, let n = 3 and by
using (1), ..., (8) of Lemma 3.4 we have
{H(24),H(25),H(26),H(27),H(28),H(29),H(30),H(31)} =
{1,0,1,0,1,0,1,0}.
Therefore we can calculate the value of each
H(n) in 3.7, and we get the following
triangle of numbers.
|
|
(3.8) |
We can make a theorem by generalizing the pattern we found in Example 3.2.
Theorem
3.1 (1) Suppose that
![]() then
then 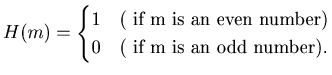
(2) Suppose that
![]() then
then 
Proof
Here we can
use the method that is similar to the one used in Example 3.2.
By Lemma 3.4 we can get the values of
H(8n), H(8n+1), H(8n+2), H(8n+3), H(8n+4),H(8n+5), H(8n+6),H(8n+7)
from the values of H(2n) and H(2n+1) for any natural number
![]() .
In this way we can prove this theorem.
.
In this way we can prove this theorem.
Example
3.3 Now we are
going to show how the pattern in
![]() and Lemma 3.3 produce the pattern in
and Lemma 3.3 produce the pattern in
![]() .
.
By Lemma 3.3
![]() is odd for any non-negative number
is odd for any non-negative number
![]() .
.
By
![]() and
and
![]() we have
we have
{H(2),H(4),H(6),H(8),H(10),H(12),H(14),H(16),H(18)}
=
{0,1,1,0,0,0,0,1,1}, and hence by Lemma 3.3
we have
{JI(2),JI(4),JI(6),JI(8),JI(10),JI(12),JI(14),JI(16),JI(18)
}
= {1,0,0,1,1,1,1,0,0}.
In this way we can calculate ![]() by
by
![]() .
.
Theorem
3.2 (1) Suppose that
![]() then
then 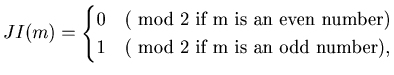
(2) Suppose that
![]() then
then ![]()
![]() .
.
Proof
We can prove
this theorem by the same method that we used in Example 3.3.
By Lemma 3.3
![]() is odd for any non-negative integer
is odd for any non-negative integer
![]() .
.
By Theorem 3.1 and Lemma 3.3
we can get the values of
![]() for any natural number
for any natural number
![]() .
.
Example
3.4 Figure (3.1) is the graph of the list {JI(n) ,
![]() ,
3, ..., 256} and Figure (3.2) is the graph of the list {JI(n) ,
,
3, ..., 256} and Figure (3.2) is the graph of the list {JI(n) ,
![]() ,
3, ..., 1024}. The horizontal coordinate is for the number of numbers
(or people in the original Josephus problem) involved in the game,
and the vertical coordinate is the number that remains when the game
is over. For example by
,
3, ..., 1024}. The horizontal coordinate is for the number of numbers
(or people in the original Josephus problem) involved in the game,
and the vertical coordinate is the number that remains when the game
is over. For example by
![]() we have the point
we have the point
![]() in the graph.
in the graph.
. ![\includegraphics[height=4.5cm,clip]{graph2561024.eps}](img187.gif)
Figure (3.1.) Figure
(3.2)
If we compare Figure 3.1 and 3.2, we can discover a very
interesting fact. That is the existence of self-similarity. As to the
research of self-similarity by the authors see
![]() .
.
Is
there any relation between the patterns of the sequence {![]() ,
n = 1,2,...} and the self-similarity of Figure (3.1) and Figure
(3.2)?
,
n = 1,2,...} and the self-similarity of Figure (3.1) and Figure
(3.2)?
Example
3.5 Here we
present recursive relations that have nothing to do with the Josephus
problem. First we let
![]() ,
,
![]() and
and
![]()
(1)
![]() .
.
(2)
![]()
(3)
![]()
(4)
![]()
(5)
![]()
(6)
![]()
(7)
![]()
(8)
![]()
If we calculate
![]() for
for
![]() we get {1, 1, 3, 4, 3, 7, 1, 3, 9, 1, 11, 7, 11, 9, 9, 13, 5, 11, 7,
13, 11, 15, 9, 25, 1, 23, 3, 29, 3, 31, 1, 11, 25, 9, 27, 7, 35, 9,
33, 3, 41, 1, 43, 7, 43, 9, 41, 25, 25, 25, 27, 15, 43, 17, 41, 33,
25, 31, 27, 31, 35, 33, 33}. In these numbers 4 is the only even
number. In fact this is the only even number in {
we get {1, 1, 3, 4, 3, 7, 1, 3, 9, 1, 11, 7, 11, 9, 9, 13, 5, 11, 7,
13, 11, 15, 9, 25, 1, 23, 3, 29, 3, 31, 1, 11, 25, 9, 27, 7, 35, 9,
33, 3, 41, 1, 43, 7, 43, 9, 41, 25, 25, 25, 27, 15, 43, 17, 41, 33,
25, 31, 27, 31, 35, 33, 33}. In these numbers 4 is the only even
number. In fact this is the only even number in {![]() ,
,
![]() }
by the calculation of the computer algebra system Mathematica.
}
by the calculation of the computer algebra system Mathematica.
Figure (3.3) is the graph of the list {F(n) ,
![]() ,
3, ..., 256} and Figure (3.4) is the graph of the list {F(n),
,
3, ..., 256} and Figure (3.4) is the graph of the list {F(n),
![]() ,
3, ..., 1024}.
,
3, ..., 1024}. ![\includegraphics[height=4.5cm,clip]{graphF.eps}](img202.gif)
Figure (3.3.) Figure
(3.4)
The sequence {F(n)
![]() ,
n = 1,2,...} = {1,1,1,0,1,1,1,...} does not have any interesting
pattern, but the graph of it has the self-similarity. By this example
we know that a sequence can produce a graph with the self-similarity
even if it does not have any interesting pattern when reduced by 2.
Therefore the authors think it is almost sure that there is not any
relation between the pattern of sequence in 3.2
and the graph that is produced by it.
,
n = 1,2,...} = {1,1,1,0,1,1,1,...} does not have any interesting
pattern, but the graph of it has the self-similarity. By this example
we know that a sequence can produce a graph with the self-similarity
even if it does not have any interesting pattern when reduced by 2.
Therefore the authors think it is almost sure that there is not any
relation between the pattern of sequence in 3.2
and the graph that is produced by it.
Acknowledgments
Contributions from Hiroshi Matsui, Soh Tatsumi and Takahumi
Inoue. Although they were not the primary authors, their
contributions were significant. We would like to thank Mr. Harrison
Gray for helping us to prepare this article.