Non-linear Fractal Interpolating FunctionsR. Kobes, H. Letkeman Abstract:We consider two non-linear generalizations of fractal interpolating
functions generated from iterated function systems. The first corresponds
to fitting data using a
Kth-order polynomial, while
the second relates to the freedom of adding certain arbitrary functions.
An escape-time algorithm that can be used for such systems to generate
fractal images like those associated with Julia or Mandelbrot sets is also
described.
IntroductionAn Iterated Function System (IFS) can be used to construct a fractal interpolating function for a given set of data [1,2]. The simplest such system defines an IFS with coefficients an, cn, en, and fn determined from discrete data points (ti, xi), i = 0, 1,..., N. Such an IFS interpolates the data set in the sense that, under certain assumptions on the coefficients [1], the attractor of the IFS is a graph that passes through the data points. In this particular case, the IFS of Eq. (1) uses a linear (in t) function between adjacent points to interpolate the data.Various generalizations of fractal interpolating functions have been considered, including those for higher dimensional functions, the use of hidden variables, and extensions to certain non-linear distortions [3,4,5,6,7]. In this note we describe a generalization whereby the transformation incorporates a Kth-order polynomial (in t) interpolation. We also discuss certain classes of non-linear functions that can arise in such interpolating functions, and show how such functions can, with the use of a particular escape-time algorithm, be used to generate fractal images. We first review
the construction of a linear fractal interpolating function. Suppose we
have data points (ti, xi), i = 0...N, describing a function
x(t). Consider the IFS of Eq. (1) and impose,
for n = 1, 2,..., N,
This leads to determination of the coefficients as
whereby the transformation of Eq. (1) can be
written as |
cn = 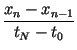 - - 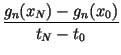 , fn
= , fn
= 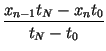 - - 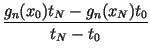 . . |
(6) |
| xn | xn + gn(x) - gn(xN) | ||
| xn - 1 | xn - 1 + gn(x) - gn(x0). | (7) |
Quadratic and Higher Order Interpolating
Functions
The interpolating function of the last section used a
linear (in t) approximation between adjacent points. In this
section we indicate how a quadratic, and then arbitrary Kth-order polynomial,
approximation may be constructed. Let us consider a transformation of the
form | Wn(t) | = | ant + en | |
| Wn(x) | = | cnt + dnt2 + fn | (8) |
and impose the conditions, for n = 2, 3,..., N, The point tm is determined as with corresponding point xm. The coefficients of the IFS are determined as
| an | = | 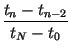 |
|
| en | = | 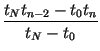 |
|
| cn | = | 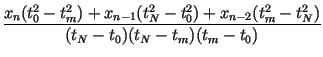 |
|
| dn | = | 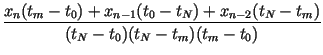 |
|
| fn | = | 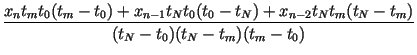 |
(11) |
With this, the transformation can be written as
which thus uses a quadratic (in t
As in the previous section, including an arbitrary function
gn(x) in the IFS transformation via
is straightforward. The conditions (9) leads to determination of the point tm of Eq. (10) as before, together with the accompanying point xm. The transformation itself has the same form as Eq. (12) with the following replacements:
| xn | xn + gn(x) - gn(xN) | ||
| xn - 1 | xn - 1 + gn(x) - gn(xm) | ||
| xn - 2 | xn - 2 + gn(x) - gn(x0). | (14) |
From these considerations, the pattern to constructing a Kth-order fractal
interpolating function is apparent. Start with a transformation of the
form
and impose the conditions, for n = K, K + 1,..., N, which determine the coefficients Bn(i) of Eq. (15), as well as the K - 1 intermediate points tmj, j = 1, 2,..., K - 1 and corresponding xmj points. The resulting transformation will be of the form given by Lagrange's formula for a Kth-order polynomial interpolating function constructed from K + 1 points:
| Wn(t) |
= | 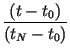 tn + tn + 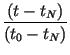 tn - K tn - K |
|
| Wn(x) |
= | 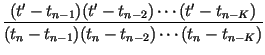 xn + xn + |
|
| + | 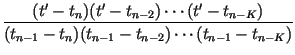 xn - 1 +...+ xn - 1 +...+ |
||
| + | 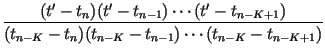 xn - K xn - K |
(17) |
The inclusion of an arbitrary function gn(x) in the transformation Wn(x) of Eq. (15), as was done for the linear and quadratic transformations of Eqs. (5) and (13) respectively, is straightforward. As might be expected, the use of these higher-order interpolating functions can increase the accuracy of the interpolation significantly, at least for smooth functions. As an informal example, consider the interpolation of the function x4exp(- x)cos(x) - a comparison of the relative error using a linear vs. a quadratic interpolation function appears in Fig. 1, where it can be seen that the a quadratic interpolation offers an order-of-magnitude improvement in the fit over most of the range.
![\includegraphics[width=3.375in]{error}](index_files/img71.gif) |
Escape-Time Algorithm
In this section we
describe an algorithm for generating fractal images like those for Julia
or Mandelbrot sets from IFS interpolating functions. As well as allowing
one to associate fractal images with discrete data sets, this will also
offer another comparison of the detail available from linear
vs. higher-order fractal interpolation functions.
Suppose we have an IFS transformation Wn(t,
x), generated by some data points (xi,
yi), i = 0,
1,..., N, which includes a non-linear function
gn(x), as was done for the linear and quadratic
transformations of Eqs. (5) and (13)
respectively. We now continue the real variable x of this
transformation to complex values: x![]() z =
(zR, zI), in effect defining a complex
map:
z =
(zR, zI), in effect defining a complex
map:
| tn + 1 | = | antn + en | |
| zn + 1 | = | Bn(0) + Bn(1)tn + Bn(2)tn2 +...+ Bn(K)tnK + gn(zn) | (18) |
for n = 0, 1,..., N. We can then, in analogy with the algorithm used for Julia sets, define the following escape-time algorithm to generate a fractal pattern:
- for each pixel in a region of interest
- initialize t
- initialize z = (zR, zI) to the pixel coordinates
- for n = 0, 1,...,
N
- calculate (
t
 , z
, z ) =
Wn(t, z)
) =
Wn(t, z)
- break if
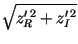 exceeds a maximum
exceeds a maximum
- set (t, z) = ( t
 , z
, z )
)
- calculate (
t
- end for
- plot the pixel
- end for
The arbitrariness of the function gn(x) and
the data set (ti, xi) used to fix the
IFS leads to a wide variety of possible fractal images. An interesting
class of functions gn(x) to consider are those
for which, when continued to the complex plane x![]() z = (zR, zI), lead to
a map having a fixed point zI*
= 0 = Imgn(zR,
zI*). In such a case one could augment the
usual condition of the escape-time algorithm to cease iteration:
z = (zR, zI), lead to
a map having a fixed point zI*
= 0 = Imgn(zR,
zI*). In such a case one could augment the
usual condition of the escape-time algorithm to cease iteration: ![]() >
> ![]() , where
, where ![]() is some suitably large value, to also cease
iteration when | zI|
<
is some suitably large value, to also cease
iteration when | zI|
< ![]() , where
, where ![]() is a suitably
small value. The coloring algorithm used to plot a pixel, which depends on
the number of iterations attained when this break-out condition was met
(if at all), will then lead to structure in the region where the break-out
condition on the magnitude of z is not met.
is a suitably
small value. The coloring algorithm used to plot a pixel, which depends on
the number of iterations attained when this break-out condition was met
(if at all), will then lead to structure in the region where the break-out
condition on the magnitude of z is not met.
We give two examples of fractal images generated this way for the choice gn(x) = - 0.4x + 0.5x2 + 0.2x3, with the data generated from the logistic map xn + 1 = 3.4xn(1 - xn), with n = 0, 1,...60. The first one, appearing on the left in Fig. 2, corresponds to the generalization Eq. (5) of a linear (in t) fractal interpolating function, while the second image on the right of Fig. 2 corresponds to the generalization Eq. (13) of a quadratic (in t) interpolating function. A coloring algorithm that simply mapped a color to the number of iterations attained when the break-out condition became satisfied was used in both cases.
These figures illustrate, in the interior of the fractal object, the richer structure arising from the quadratic over the linear interpolation function. In this region the break-out condition | zI| <
Conclusions
We considered two non-linear
generalizations of fractal interpolating functions constructed from
iterated function systems. One - using a
Kth-order interpolating
polynomial - can potentially improve the accuracy of fractal interpolating
functions. The other - use of certain arbitrary functions in the IFS -
can, together with an appropriate escape-time algorithm, generate fractal
images of the type associated with Julia or Mandelbrot sets.
This work was supported by the Natural Sciences and Engineering Research Council of Canada.
Bibliography
- 1
- M. F. Barnsley, Fractals Everywhere (Academic Press, San Diego, CA, 1993)
- 2
- H. O. Peitgen, H. Jürgens, and D. Saupe, Chaos and Fractals - New Frontiers of Science (Springer, New York, 1992).
- 3
- M. F. Barnsley, J. Elton, D. Hardin, and P. Massopust, Hidden Variable Fractal Interpolation Functions, SIAM J. Math. Anal. 20 (1989), 1218-1242.
- 4
- P. R. Massopust, Fractal Functions, Fractal Surfaces and Wavelets (Academic Press, San Diego, CA, 1994).
- 5
- L. M. Kocic and A. C. Simoncelli, Fractal Interpolation in Creating Prefractal Images, Visual Mathematics 2, No. 2 (2000).
- 6
- H. O. Peitgen and D. Saupe, The Science of Fractal Images (Springer, New York, 1988).
- 7
- E. Gröller, Modeling and Rendering of Nonlinear Iterated Function Systems, Institute of Computer Graphics, Technical University of Vienna Report TR-186-2-94-12 (1994).
- 8
- J. Barrallo and D. M. Jones, Coloring Algorithms for Dynamical Systems in the Complex Plane, Visual Mathematics 1, No. 4 (1999).
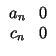
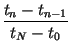 ,
,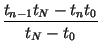
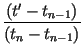 xn +
xn + 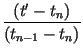 xn - 1
xn - 1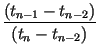 tN +
tN + 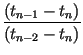 t0
t0 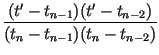 xn +
xn + 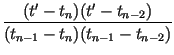 xn - 1
xn - 1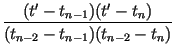 xn - 2
xn - 2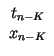
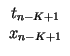
![\includegraphics[width=2.75in]{ifs1}](index_files/img78.gif)
![\includegraphics[width=2.75in]{ifs2}](index_files/img79.gif)