|
By Ph.D.
Faculty of Architecture & Town Planning,
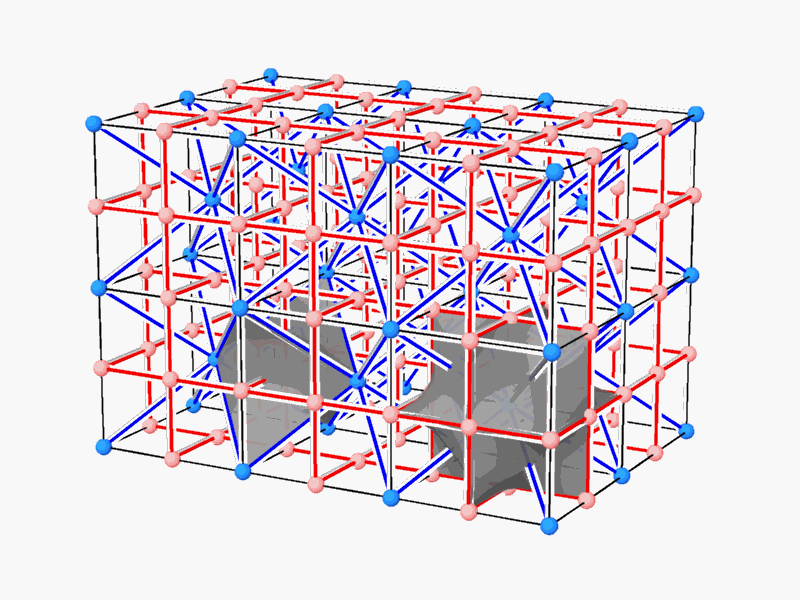
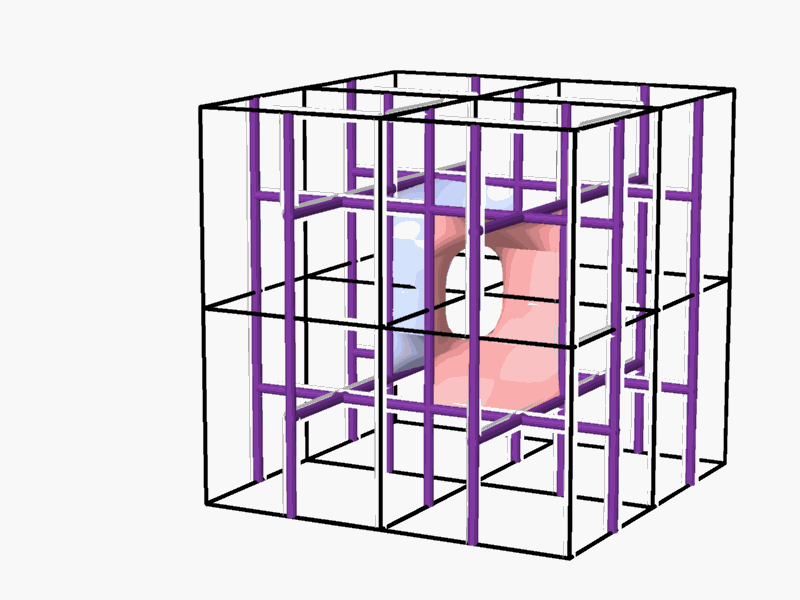
Abstract The issue of space partitioning underlies the architectural planning and design of buildings, structures and spaces intended for human activity. This thesis explores the phenomenon of periodic dual spaces, the periodic three-dimensional networks that represent their inner structure and the partition between them. It is assumed that every dual-pair of networks, (often referred to as complementary or reciprocal pairs), (Figure 1) can be separated and partitioned by a continuous smooth hyperbolic surface.
Figure 1 - two dual networks
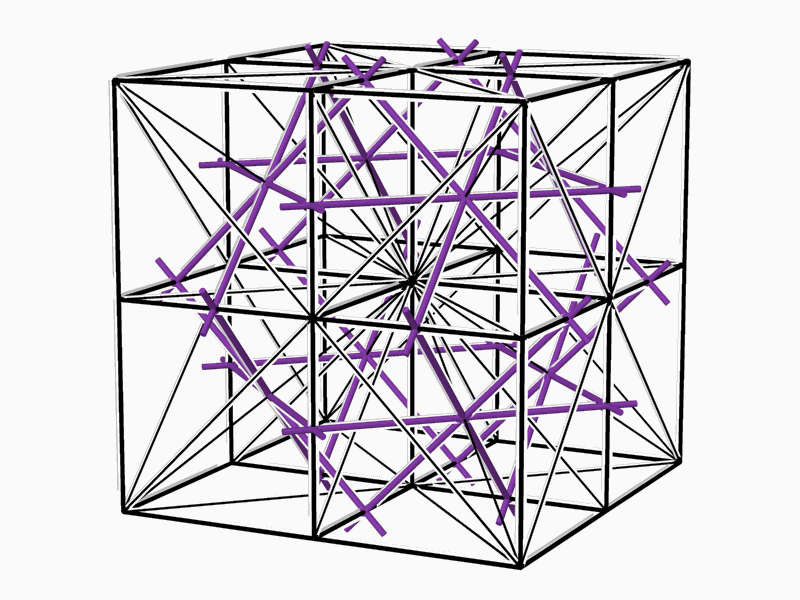
The thesis is focused on the unique phenomenon of identical dual spaces and the related network pairs, and the hyperbolic surface-partitions separating them, and thus dividing the entire space into two identical (complementary) sub-spaces (Figure 2). The adopted approach implies investigation of order and organization of these spaces and related parameters, their inner and overall symmetry structure and the nature of the 2-manifold partitions, dividing between them. 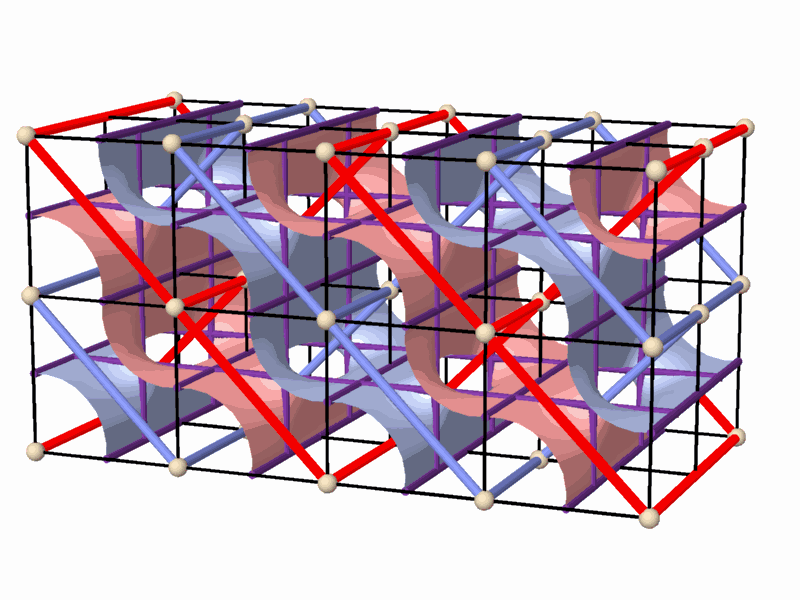
Figure 2 An additional central goal was to conduct
a systematic exhaustive search of possible (thus defined) surface-partitions,
in order to establish their range of existence and to facilitate their
classification. The study described in this thesis comprises three stages.
1 Topological attributes of smooth 2-manifold which divide the space into two identical
subspaces.
The first stage consisted of studying
identical dual spaces, their properties and parameters trying to develop
insights into their nature and order.
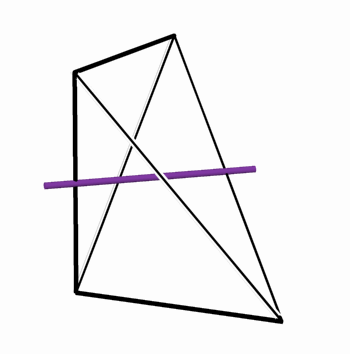
Figure 3
The tunnel-like periodic spaces, represented by networks, are defined within the Euclidean three-dimensional space, and are composed of periodic cells. This property indicates the relation between the network-pairs,| and the surface separating them, and the symmetry groups acting on this space. The smallest repetitive cell, called "Elementary Periodic Region" (E.P.R.) (Figure 3), is derived from a periodical space using the symmetry operations of the symmetry group that acts on this space. The E.P.R. contains complete representation of all the phenomena taking place within the "periodic complex" and particularly, representation of the whole periodic space, its symmetry group, the two complementary (identical) subspaces, the self dual lattice-pairs characterizing them, as well as the surface partition in between. At this stage of the research, the topological properties of smooth 2-manifolds in general, and of smooth 2-mainfolds which divide the space between two dual networks in particular, were explored. The main properties of these 2-manifolds are (Figure 3): * They are smooth, periodical and hyperbolic, and exist in the three-dimensional space. * They divide the space into two identical subspaces that graphically represent two interwoven and
non-intersecting tunnel-networks. The two complementary tunnel systems
are identical in volume
and shape, and their tunnel axes form two identical, three-dimensional
space networks.
* 2-fold rotation axes contained within the 2-manifold rotate one subspace
into the identical complimentary
subspace, forming in it a periodic (three-dimensional) space network,referred
to as a "2-fold network".
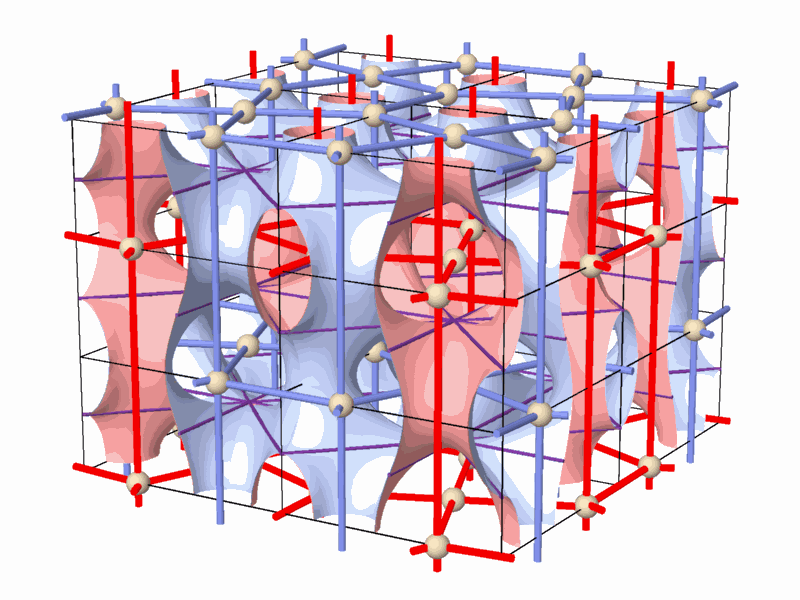
Figure 4
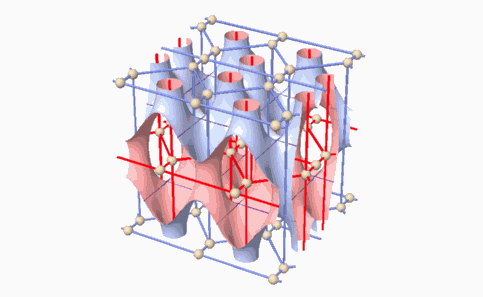
2 The method of searching and classifying of the 2-manifold. In the second stage, a method for the enumeration and classification of the 2-manifolds that divide the space into two identical subspaces and identification of the axes of the identical dual tunnel networks was developed. The method of enumerating the 2-manifolds was based on their topological properties that were studied in the previous stage. The issues of periodic minimal hyperbolic
2-manifolds that divide the space into two identical subspaces were investigated
in the past. Seven surfaces were found (Figure 4).
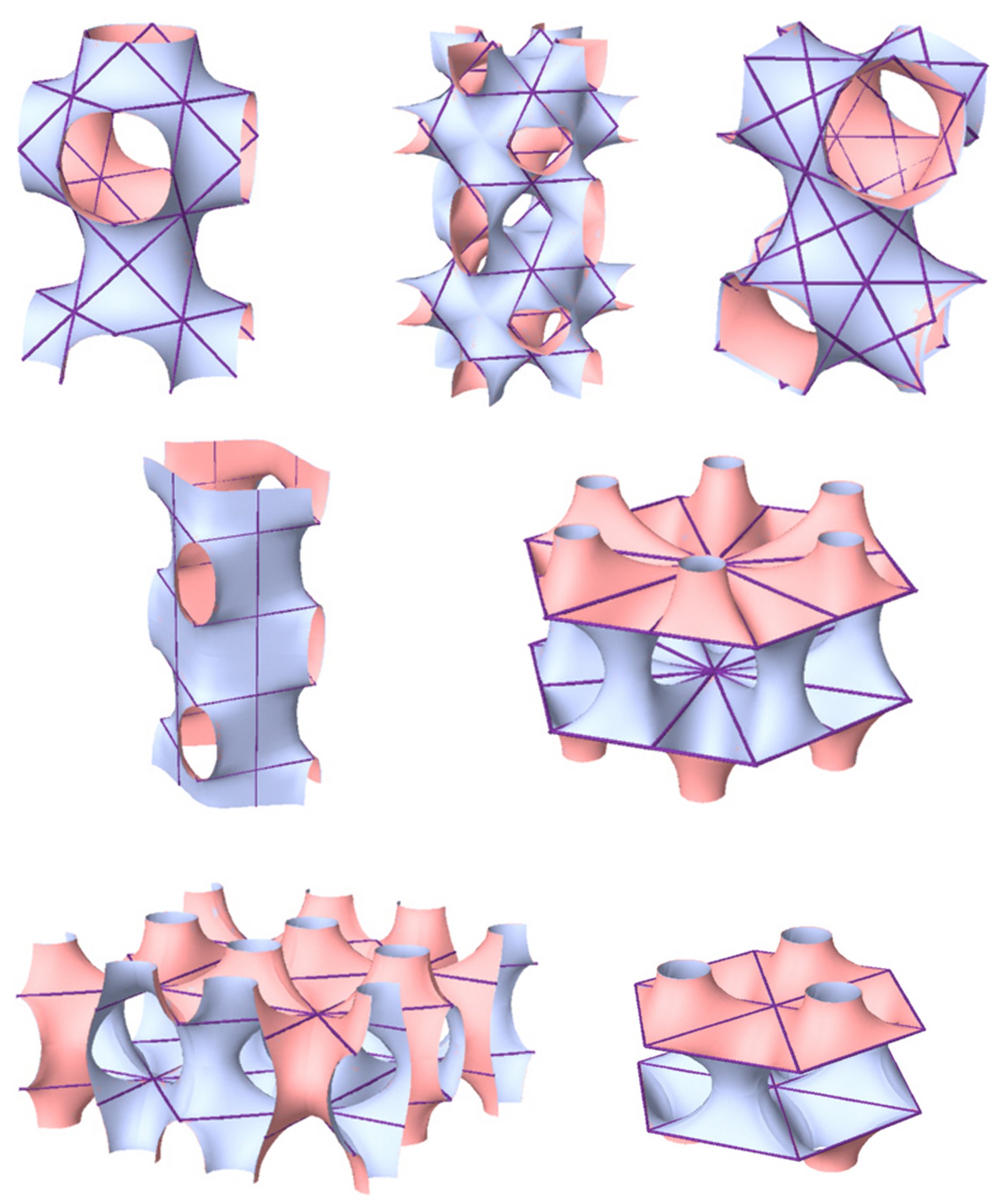
Figure 5
It was clear even then that numerous identical networks and a smooth hyperbolic partition dividing them could be put through every E.P.R. containing 2-fold axes. No attempt has been made to date either to construct or characterize these surfaces or to define the range of their existence and to provide their classification. The existence and periodicity of the 2-manifolds that divide the space into two identical subspaces in the Euclidean three-dimensional space indicate the link between these 2-manifolds and the symmetry groups operating within this space. The "atomistic" conception of space suggests the existence of an E.P.R. that represents all the properties of the complex. Finding all the E.P.R.s, which represent identical-dual spaces and the 2-manifold in between them, leads to discovery of the 2-manifolds. The number of the different E.P.R.s is finite due to the fact that the number of symmetry groups, which operate in the Euclidean space is finite. The method for the enumeration and classification of the 2-manifolds consists of several consecutive steps. * Locating all the E.P.R.s derived from the symmetry groups (Figure 5).
* Reducing the list of the relevant E.P.R.s to those containing 2-fold
axes, capable of rotating the E.P.R.
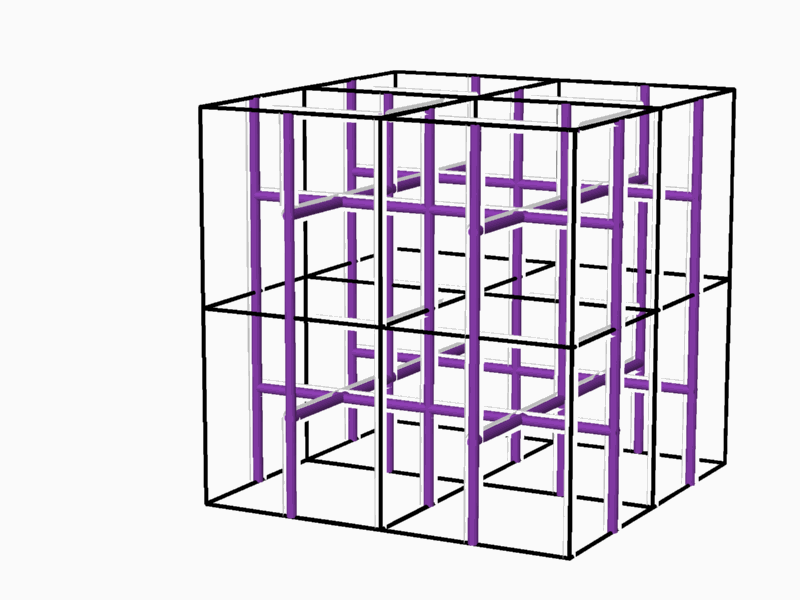
*Obtaining the 2-fold networks by repetitive duplication of the E.P.R.s found in the previous stage (Figure 7). * Locating
periodic cells enclosed in the 2-fold networks (more than one is likely),
(which may enclose a periodic
* Duplicating the periodic cells with the enclosed periodic unit of the
2-manifolds, until a large enough section
* Topologically enumerating each of the 2-manifolds, according to their
respective tunnel network.
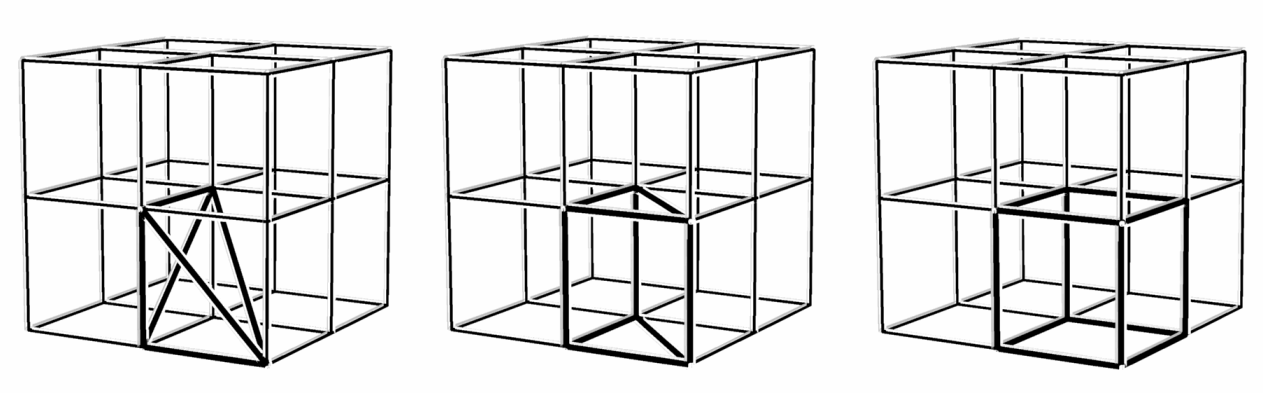
Figure 6 - E.P.R.s containing 2-fold axes, that rotate the E.P.R. into itself
Figure 7 - Two different 2-fold networks
Figure 8 – Two different periodic cells located in the same 2-fold network 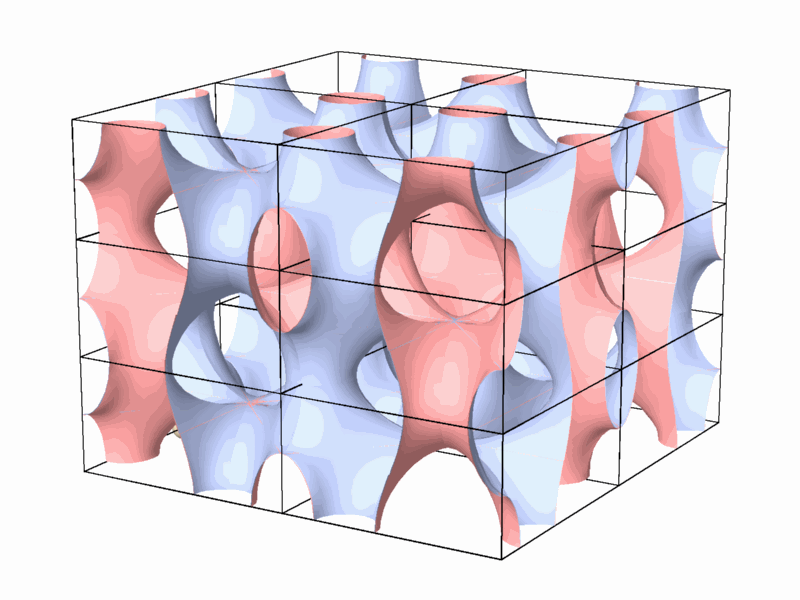
Figure 9 3 The
process of searching and classifying of the required 2-manifold.
In the third stage, by applying the previously developed
method, a process of the actual identification of the self-dual spaces
was carried out.
Finding the 2-fold networks is supposed
to be exhausted at this stage. The method of locating the 2-fold networks
is based on identifying the E.P.R.s that may, as stated earlier, contain
2-fold axes that rotate them into themselves.
At this stage fourteen different "2-fold
networks" were found. Among those, twelve were found to contain seventeen
different closed periodic cells, which may enclose a periodic unit of a
2-manifold.
Duplicating these closed cells led,
to the discovery of eight topologically different 2-manifolds. Among them,
a new 2-manifold, unknown to date, was discovered. (Since then, yet another
2-manifold was discovered) (Figure 10).
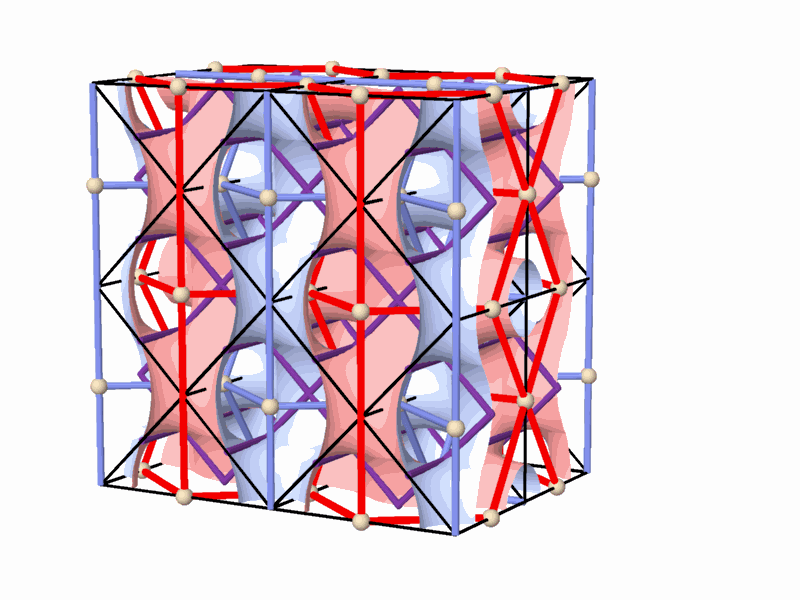
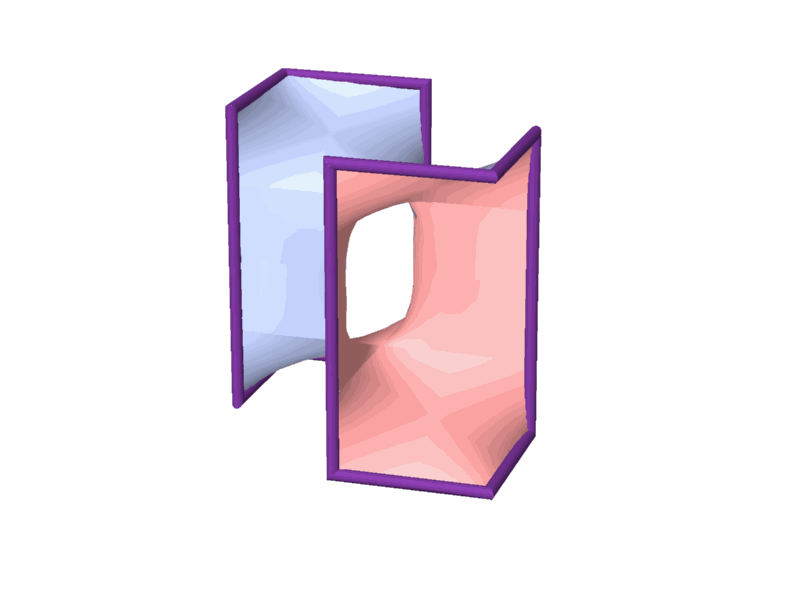
Figure 10 - A new 2-manifold that was discovered.
Among the seventeen different closed periodic cells, mentioned earlier, there are six closed cells that consist of a "split perimeter". These "split perimeters" can enclose a "periodic 2-manifold unit" of different category surfaces, i.e. they can enclose in the periodic closed perimeter cell a successive smooth hyperbolic "periodic 2-manifold unit", which is topologically different from the minimal "periodic 2-manifold unit" previously discovered. Thus a new class of 2-manifolds, designated "The Multiple- Sleeved Class" was found (Figure 11). This class contains an infinite number of topologically different 2-manifolds. This indicates that the tunnel axes of these 2-manifolds represent pairs of identical-dual networks that differ from each other.
Figure 11 The proposed method of identifying the 2-manifolds that divide between pairs of self-dual networks, led to the discovery of new 2-manifolds in addition to the seven 2-manifolds, of which two were first discovered by Hermann Amandus Schwarz (1843-1921). The 2-manifolds were looked for in representative groups, relating to symmetry groups, the number of which is finite. This does not necessarily mean that the number of 2-manifolds, and/or the number of self-dual pairs of networks are also finite. References A. Korren, (2003) Identical Dual
Lattices and Subdivision of Space. Ph.D. Thesis.
Technion – Israeli Institute of Technology.
|