|
INTERVAL
SYMBOLISM
1. In some instances, intervals may
be taken as a factor in the creation of form. In movements I and II of
this Sonata, it is to be observed that just about every formal plane is
welded into a unified sonority by a characteristic interval, or combination
of intervals, being used in an organum-like way or as parallel chords (on
occasion thematically). In movement I in particular, this produces the
"layered" effect of its cross-section. (Why this technique should be linked
particularly to movement I is a question about which the chapter on "Meaning"
gives information.)
2. Systematic expansion and contraction
of intervals permeates nearly every part of movements I and II. This
expansion and contraction has the character of a dynamic process,
and coincides with the ebb and flow of the work's form and content. For
example in movement I, there is a process of expansion throughout the exposition
and the first half of the development section, while in the second half
of the development and the recapitulation, there is one of contraction.
The main forms in which this manifests
itself are summarized below:
a) Sequential entries of motives,
or the melody notes themselves, systematically succeed one another in expanding
or contracting intervals (e.g. in movement I the funnel-shaped progressions
in bs. 208 - 217 and 239 - 247).
b) The voices open or close like
a pair of scissors (e.g. movement I bs. 256 - 263).
c) Sections of themes periodically
expand or contract their range (e.g. movement I, first subject bs.
32 - 40).
d) By a systematic expansion
and contraction of scales, chromatic becomes diatonic, diatonic
becomes pentatonic, pentatonic becomes motives based on fourths and fifths,
the latter on occasion expanding to motives based on sixths - plus the
reverse of all these (e.g. movement I, second subject bs. 84 - 105, and
movement II, the chant bs. 48 - 56).
e) By a systematic expansion
or diminution of the intervals of equidistant chords, chromaticism
becomes whole-tone scale, whole-tone scale becomes diminished seventh chord,
diminished seventh chord becomes augmented triad, and augmented triad becomes
augmented fourth-chord, the latter evolving into the circle of fifths or
fourths, or rather the fifth-chords and fourth-chords made from it - and
again all this in reverse (e.g. the voice entries in movement I bs. 175-190
follow this principle).
To this process of interval expansion
and contraction will be ascribed (in the chapter on "Meaning") a certain
irrational significance, giving it a psychological emphasis, as
being projections of the movements and dynamism of levels at the subconscious.
This resembles the significance ascribed earlier to chromaticism, to illustrate
which we might again refer to the Mad Scene in Boris Godunov. In
movement III, by contrast, no trace of these processes is found - unlike
in the turbulent first movement - the third movement radiating throughout
an undisturbed gaiety.
3. Basic acoustical attributes, and
also in part the images entrenched in us by classical harmony, mean that
intervals have acquired a number of qualities which seem to have had an
important influence on Bartók's usage.
Thus the perfect fifth, and its
inversion the perfect fourth, due to its being one of the
nearest harmonics, and having a strong individuality, is so pervasive in
the entire Sonata, both vertically and horizontally, not to mention the
compositional principle of answering at the fifth, that it seems almost
superfluous for an analyst to dwell further on a fact so conspicuous. In
essence, the sentence in the chapter on tonal organization which says that
Bartók's tonal system fits comfortably the groundplan of the circle
of fifths or fourths needs to be emphasized. The downward leaping
fourth aspect is every bit as energetic here as the simultaneously sounding,
or upward leaping fifth (in support of this we would refer to the themes
of movement III bs. 19-20, 44-45, 176-177).
The sixth can be seen as an enlarged
fifth, one self-expanded and overstrained by an extra degree. This is doubtless
why in movement I, the sixths in the closing theme of the exposition, and
the fugue subject have such an intense effect (bs. 105, 332). An important
point is the fact that the sixth above the tonic is mostly climactic
(it is enough to refer to these culminatory points: movement I, first subject
b. 37, and the development b. 217). The sixth above the tonic is often
treated in this way in classical melody types (e.g. the fugue subjects
of Bach!).
The relationship between the "expansive"
major
third and the "anxious" minor third is a specially contrasted
one. The major third tends, after all, to be associated with the "spacious"
major, and the minor third with the "confined" minor triad.
The character of the augmented fourth
(diminished fifth) is determined by its perfect, indeed absolute, intertonality
and acoustical rootlessness, which means it can be used to create the most
extreme polar opposites (in the axis system the pole-counterpole relationship).
It is this quality which elevates the polarity of the augmented fourth
to being one of the central structural principles of this Sonata. Here
we should add that Bartók was painfully sensitive to the 11th overtone,
which at a distance corresponds to the tritone of the fundamental (and
determines the Lydian sound of the overtone chord). 11)
It should be noted that such characteristics
of intervals can be exhibited clearly only in themes which are "12-tone"
and completely chromatic in character, since their behaviour is free of
the influence of the classical harmonic system.
4. In the matter of interval symbolism,
without doubt the most interesting find is provided by an analysis of movement
II bs. 48-56, where - on the border between a microworld and a macroworld
- the relationship between the minor third and the perfect fourth
offers us a key to transposing between the chromatic and diatonic systems.
It becomes clear that the minor third is inseparably associated
with chromatic motive work, and the perfect fourth with diatonic.
12)
At the same time, it is the first clue in this analysis that points towards
the formation of comprehensive unity in the Sonata. For the contrasting
of "spacious" and "narrow" arises not as a method of treating in isolation
the question of form, but constitutes an integral intellectual and logical
unity with the programmatic conception of the work.
5. Summed up, what has been said so
far produces the following result: the parallel chords used by Bartók,
together with consecutive intervals, characteristic melodic pitch ranges,
a dogged use of particular intervals, and repeatedly recurring intervallic
leaps employed as basic figures, form a self-contained system, which
corresponds to this order of magnitude:
major second, minor third,
perfect fourth, minor sixth, minor ninth.
This arrangement is characterized by
the fact that its components stand in a golden section relationship
with one another (see in more detail the chapter on the proportions of
the Sonata). For the sequence major second - minor third - perfect fourth
- minor sixth - minor ninth produces, if counted in semitones, the
simplest
numerical relationships of the golden section:
2 : 3 : 5 : 8 : 13
(2 = major second, 3 = minor third,
5 = perfect fourth, 8 = minor sixth, 13 = minor ninth). This should provisionally
be conceived as if, to build a house, only beams 2, 3, 5, 8 and 13 metres
long were available. The builder is free to make use of any of them, but
he cannot change their measurements. In this sequence, known as the Fibonacci
numbers,
each number is equal to the sum of the previous two 13)
(thus the sequence continues: 21, 34, 55, 89 etc.). A good example of this
is the various changes of shape and compass of the main theme in movement
III of the Divertimento:


Even the intervallic
cells divide up according to the above progression of quantities. For example,
8 can only split into 5 + 3, the alternatives 4 + 4 and 7 + 1 being excluded
from the system.
It is striking
that the analyst hardly encounters any parallel major thirds or
major
sixths; it is almost as though there were a ban on consecutive major
thirds and sixths. All the more frequent and widespread is the occurrence
of consecutive minor thirds, perfect fourths, and minor sixths
(see
movement I of the Sonata). The major third has no melodic function
worth mentioning. Naturally enough, though, the motivic role of the minor
third is almost only too obvious:

The figures based
on the minor third and perfect fourth outlined in paragraph
4 are also none other than basic elements of the system. Hence the relationship
between them is accommodated to the golden section.
The notation of
parallel
major chords fits this principle for the most part (in movement I of
the Sonata), in that the structural role of perfect fourths and
minor
sixths is emphasized:

This, it would
appear, is the reason why, when Bartók writes a triad in a chromatic
piece, it has its minor third "upwards" (in second inversion), and
has its major third "downwards" (in first inversion):

The most characteristic
Bartók chord was born out of a fusion of the two; this "major-minor"
shape, made out of a minor third - perfect fourth - minor third (3:5:3),
is well known:


If consideration is given to the fact
that the pentatonic scale, in particular the la pentatonic,
rests primarily on a framework determined by the perfect fourth, minor
third and major second, then pentatony must be seen as the purest
musical expression of the golden section.

Does this not
mean that instinctively, in one of mankind's most ancient artistic utterances,
form was given to the law of the golden section? The most ancient layer
of folk music shows beyond doubt that the golden section is a law intrinsic
to music, and not one applied from outside.
In this case,
the major-minor configuration mentioned above is nothing less than an extension
and magnification of the pentatonic l - s - m - r shape; its projection
into a broader dimension:

6. a (alpha)
type harmony - b
(beta), g
(gamma), d
(delta).
The above chord
is found at every step in this form also:

This chord (which
may be considered c major-minor seventh chord) is related to a number
of others which are highly characteristic, and which as a group will be
called a chords. First of all, also in the tonality of c, there
is this common shape:
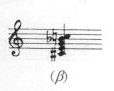
This sounds as
if the earlier major-minor chord (g) had been extended by a lower minor
third, the c# (the upper minor third in turn being omitted).
On occasion, a minor third cell is joined also from the top:

All three configurations
have in common that they are framed by a major seventh, that they consist
of minor third (3) and major second (2) cells, and that they
have the tonality of c; their tonality is provided by the prominently
sounding perfect fourth (5):

Accordingly, the
minor
third cells of the a chords are always based round the core of a fourth:

These a
type chords will be called individually b, g
and d
chords (b
corresponding to a root position, g
to a first inversion and d
to a quasi second inversion). The large a
chord shown above incorporates the b,
g
and
d alternatives.
Equally characteristic are these reduced forms:
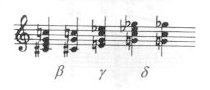
The 4th alternative, e
(bb
-c-eb-f#-a),
due to its unstable tonality is hardly used.


The basic principle therefore is the
following: in order to establish a feeling of tonality, at least 2 notes
are required, the simplest case being the root (e.g. c) and its
fifth (g):

The note g here reinforces the
c, whereas by itself the g has a dominant meaning (tonality
can after all only be supported by means of the asymmetrical division
of the tonal system; in the case of a division based on equidistance, it
is not possible to know which note to keep to). If this principle is transferred
to the relationships of the axis system, then it is found that the note
g
can be substituted by any note of the dominant axis without changing the
c
tonality:

(The first 3 alternatives are not new
to us, since they correspond to the constituents of the dominant seventh
chord).
Similarly, the note c can be
replaced by any note of the tonic axis without the function being changed:

The only proviso
is that the chord should be made up of two levels: that of the tonic
and that of its defining dominant. The a chord is thus no more than the
axis extension of the simple c-g relationship. In place of c
we have the tonic axis, and in place of g, the dominant axis:
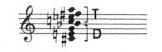
To build an even
larger a chord, it is necessary that the pattern 2 + 3 + 3 + 3 be repeated
periodically, as follows:
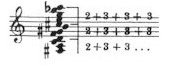
Given some latitude,
figures in which 2 + 3 + 3 is repeated periodically can also be taken to
be a chords, e.g. this:


The use of a chords is just as widespread
in the music of Bartók as was for example the seventh chord in the
classical style.
There remain two important groups left
to discuss in the list of chords constructed following the golden section
(GS).
7. Equidistant patterns.
In what follows, the whole-tone scale
will
have the symbol w (omega
- the letter farthest from a in the alphabet; this has been chosen deliberately,
since these kinds of music are used by Bartók as contrasts, a
being "ardent", w
"neutral"). Because the 12-tone system only permits of two whole tone constructions:

any further patterns
being inversions of these, then one w will be the dominant of the other.
Like the w, the diminished seventh and the fourth chord have an equidistant
shape. It should be noted that when fourth chords are placed together
following the 2 : 3 principle:

then the tonic
is the one lying a major second higher or a minor third lower than the
other. Reduced to its essentials, we can see in the following cadential
turn a form of this resolution:

The
w chord is characterized
by the number 2, the diminished seventh chord by the number 3 and
the fourth chord by the number 5, because taken individually these chords
are made merely out of the major second (2), the minor third
(3) or the perfect fourth (5). None of them is in itself a GS structure,
since the GS always expresses a relationship, a relationship automatically
excluded by the equidistance. Even so, in their relationship to each
other (2:3:5), as in their relationship to the complete Bartókian
tonal system, these chords form a GS type (see §8). The augmented
triad therefore - in Bartók's chromatic system - can only exist
in the form of minor sixth + minor sixth (8 + 8).
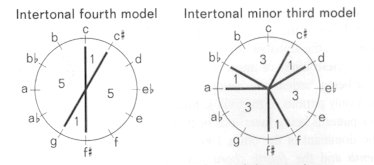
8. Intertonal
fourth models, minor third models and major second models (1:5,
1:3, 1:2).
The use of the proportions 1:5 and
1:3 in partnership is one of the oldest architectural formulas,
used already by the Chaldeans (the remains of the city of Ur), and later
playing a primary part in Gothic art. To anyone at all acquainted with
Bartók's music, these formulas will be quite familiar:

The first arises from the endless
repetition of the proportion 1:5, the second similarly from the proportion
1:3. These two patterns, it should be known, appear in Bartók almost
always as a pair of proportions harnessed together, since taxonomically
they are correlative (5:3). In this analysis, the formula 1:5 will be referred
to as the intertonal fourth model, and the formula 1:3 as
the intertonal minor third model. These patterns are called intertonal
because from the standpoint of 12-tone music they produce scales
which have symmetry:
(In other words
this represents a higher form of the equidistant division of the tonal
system, the division here consisting not of individual notes, but of groups
of notes.)
The intertonal
fourth model shows an axis tonality:

i.e. the notes c-g belong to
the tonality of c, and the notes f# and c# to the
tonality of f#. It is always given a tonal significance by
Bartók:

(in the first example the tonic
intertonal fourth model of c is heard, in the second the dominant
intertonal fourth model of F major 14)).
In fact, it is used in two ways, as a 1:5:1 form and as a 5:1:5 form:

The intertonal minor third model15)
plays a similar part in the chromatic system that tetrachordal outlines
do in the diatonic system; each is the exact taxonomical transposition
of the other:

In other words,
if the pentatonic scale l-s-m-r-d-l
is translated
into the language of the chromatic scale, then we arrive at this characteristic
scale:


(The intertonal minor third model will
be discussed in greater detail in the analysis of movement I of the Sonata,
b. 135.)
E x a m p l e s
Intertonal fourth models (1:5)


Intertonal minor third models (1:3)


Still remaining is the 1:2 formula type,
the "intertonal major second model", which can further be connected
to the GS along with the 1:5 and 1:3 models:

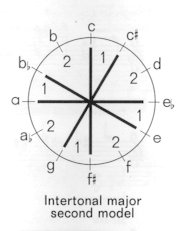

This scale can be treated as the tonic
scale in Bartók's chromatic system. Its tonality can be conceived
as consisting of the ingredients of an axis:

i.e. the tonal
resting point is always the lower note of the minor second interval
in the scale, or the upper note of the major second interval (in
this case the notes c-eb-f#-a).
16) The example below shows how the axis
system is connected to the laws of the GS 17)
:
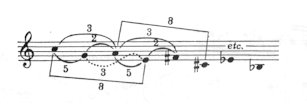
and shows also
that the concept "axis" does not mean the diminished seventh chord, but
the relationships and connections in their complex entirety of the 4 various
tonalities concealed in the intervals of the diminished seventh chord.
This means that each of the three axes creates individually a GS
system, and that transfer from one GS system (axis) to another can only
take place through a violent infringement of the laws of the GS. This is
why the main functional notes do not adhere to the first, fourth
and fifth degrees of the diatonic scale (I=T, IV=S, V=D), but (as has been
shown) are in a major third relationship to one another; transposing
a GS system (axis) by a major third thus brings about a radical cancellation
and complete disintegration of the previous system (axis), since the GS
makes no allowance for the major third.
In the tonal system
it is possible to put forward three intertonal major second models corresponding
to the three functions:

The tonic intertonal major second model
is given a special significance by the fact that it contains within itself
all the tonic (C, Eb
, F#, A) major, minor and seventh chords, the b,
g, d chords,
as well as both tonic intertonal fourth models (i.e. this model can be
made by geometrically fitting together 2 intertonal fourth models):

Apart from their common origin, chords
of the GS type are linked together by many threads. Let us try to sum them
up in a single scheme (at least their tonal forms). In the diagram below,
each example is made up of the same notes. In the 1:2 model these
notes are formed into a scale (top right hand example). The two "levels"
of the a chord are arranged in the tonal c-g relationship
(upper left hand example). In the 1:5 model the "axis" pole-counterpole
relationship is shown (lower right hand example). The lower left hand example
illustrates the connection between the axis system and the GS system.
This last example is best thought of spatially, as if the notes c-a-f#-eb separated
by a minor third (3) were on the upper rim of a cylinder, and the notes
g-e-c#-bb were
on the lower rim, the height of the cylinder (the distance between the
two rims) being a fourth (5). Each model is written in its tonic
form:
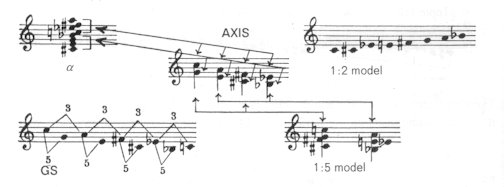
The axis system in fact is the only
means whereby the GS laws can be reconciled with the characteristic number
12 of the tonal system.
9. Chromaticism and diatonicism.
To form an accurate definition of
Bartók's use of chromaticism and diatonicism is not
an easy task, since it is not possible to identify its indications by the
concepts "narrow" and "spacious", both being equally applicable to the
laws of chromaticism.
The most general distinctive feature
of Bartók's chromaticism is that it obeys the tonal laws of GS,
while his diatonicism avoids them. The best measuring instrument for
identifying chromaticism seems to be the minor third; and
motivic material in which the minor and major third appear
as equal partners is in almost every case diatonic:

For this reason chromaticism in Bartók
tends to gravitate towards scales which are minor in character,
and Bartókian diatonicism towards scales which are major
in character (in paragraph 3 mention was made of the "anxious" quality
of the minor, and the "expansive" quality of the major).
The most spacious diatonicism
in Bartók, and the extreme example of the composer's diatonicism,
is the acoustic chord or scale:

which the present
author has called acoustic because its notes are derived from the natural
harmonic series:


To avoid unnecessary repetition, the
reader is advised to turn to the introductory section of the analysis of
movement III, without which the following cannot be understood. There
it emerges that there is a close connection between the GS system and the
acoustic system, the one being the exact taxonomic inversion of
the other. It is amazing how things spontaneously "drop out" of the whole
system. Instead of the minor third - perfect fourth - minor sixth characteristic
of the GS system (3 - 5 - 8), the acoustic scale has the major third, Lydian
(augmented) fourth and major sixth. The two systems complement each other
to the extent that the chromatic scale can be split into the GS scale and
the acoustic scale. This means that to approach Bartók's genius
as a creator of musical material is to realize the latent possibilities
and natural attractions themselves operating in the music. The two systems
represent the two sides, or double profile, of a single connected whole.
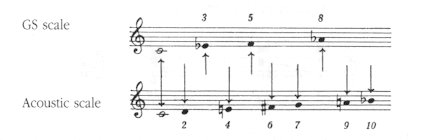
(The c#
and b, being chromatic intervals, belong to the chromatic system.)
Theoretical confirmation
is also conferred on the fact that - and this can hardly be overstressed
- the basic formula of diatonic harmony, in contrast to chromatic harmony,
is the fifth and the major third (the nearest natural harmonics!).
Also traceable to a construction based on fifths and major thirds is another
common form found in Bartók's diatonicism: the type of major chord
made of thirds whose alternate steps rhyme with one another at the fifth:
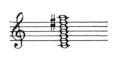

One of the patterns cut out from this
is Bartók's well-known "signature" (d-f#-a-c#), which is
also dominated by the sound of fifths and major thirds.
Mention must also be made of a third
type. The a
chord, as we know, owes its characteristic flavour to the fact
that its upper and lower levels (T and D) are in GS relationship to one
another:

If the upper and
lower levels are exchanged, however, then we immediately arrive at a "spacious"
(diatonic) effect:

in this way giving voice to the major
third and the fifth; we inevitably hear these relationships:

which in principle
are excluded from the GS system, since there can be no fifths or major
thirds in the a
chord. (Only the above two relationships can be conceived
between two diminished seventh chords.) As, in connection with the a
chords, we made a distinction between b,
g and d,
so here use can be made of the
most varied patterns of the basic type. And to make the connection complete,
the acoustic chord turns out to be a version of this latter type:

Often the root is ambiguous, both C
and F# being found:

(e.g. at the beginning
of movement III of Music for Strings, Percussion and Celesta). We might
describe as "over diatonic" the triad which has a major third above and
a minor third below (e.g. in the muted trumpets at the end of the 2nd Violin
Concerto):

This is why the
minor triads of the 2nd subject of movement III are also diatonic (from
b. 44).
Since Bartók's
chromaticism is based on the division of the tonal system along equidistant
(i.e. symmetrically) principles, then tonality must rest in principle
on 2 notes at minimum - the pole and its counterpole; in other words, it
always presupposes virtually the complete system. Connected with this is
the fact that Bartók's chromaticism is a closed system -
the "axis system" - the laws of GS also making it self-contained. By contrast,
his diatonicism - in extreme instances - is adapted to the overtones of
a single root; in other words, it is taxonomically open ended. The
one is perhaps best symbolized by the "circle", the other by the "straight
line". (It is characteristic that the axis system can only be depicted
in
a circle.) Interestingly - and this will be touched on in the chapter
"Meaning" - the axis system goes most happily with thematic material "moving
in a circle", while diatonicism usually goes with scalar or, in other words,
"straight" themes. There is also another reason for this, however. In diatonic
music, chords are constructed from the bottom upwards, a requirement not
found in chromatic music, where scales and chords are constructed both
upwards and downwards following the same principles; thus in diatonicism
there is a root note, but in chromaticism there is a central
note. In the chromatic system, everything can be inverted without the central
note losing its significance. Bartók's "mirror" passages themselves
show us how chromaticism can ignore the requirements of the harmonic series,
concepts like "up" and "down" in this context completely losing their meaning.
For example, in the recapitulation of the (2nd) Violin Concerto,
the tonality of the first subject is B, despite the fact
that the tonic B major, as a result of the inversion of the theme,
is "stood on its head", and our ears, which are conditioned to feeling
the relationships of the harmonic series, feel that the music is in e
minor (the central b is highlighted also by a pedal point):

The effect of the harmony heard below
the central b, together with its denial of the harmonic series,
is as if objects in the physical world were to suddenly cast their shadows
towards
the light.
Mathematically also, the GS system and
the acoustic system are founded upon a certain antagonism, namely that
the acoustic system (harmonic series) numerically is a ratio of whole numbers,
while the key number of the golden section is an irrational number
(0.618...; mathematically the GS proportion 13:8:5:3 is 13:8.034..., and
8:4.944..., and 5:3.090...). This means that the GS rests on geometrical
proportions; the acoustic system on mathematical ones.
Also reversed in chromaticism and diatonicism
is the relation between consonance and dissonance. Thus chromaticism is
at its most unfettered, and most neutral, when the divisions according
to the equidistance principle take it to the furthest point (a good example
being the "resolution" of movement IV of Music for Strings, Percussion
and Celesta, bs. 215-234, where the tonal system gradually clots into complete
chromaticism). To sum up, in the diatonic system everything relates to
a
single note, while in the chromatic system everything relates to the
whole system, expression being given in the latter to almost a "change
of field" for the complete tonal system.
If the reader here encounters a concept
of chromatic and diatonic not quite in agreement with that in general musical
use, then he must blame it on the fact that at the present time, there
are no technical terms available which are more suitable. Even so, it is
certain that the greatest contrast found in the music of Bartók,
and which is consciously exploited to the utmost, is the duality between
the chromatic and the diatonic, this being the purest musical
equivalent to the idea of tension and resolution. The relationship between
Bartók's chromaticism and diatonicism is like that between the Inferno
and Paradiso of Dante: taken alone, each is but a part of the Whole, and
can reveal only one side of life. Only together can the chromatic
and the diatonic form an ideal unity and a comprehensive world concept.
| Characteristics of the GS system: |
Characteristics of the acoustic
system: |
| (Bartók's
chromatic
system) |
(Bartók's
diatonic system) |
| Pentatonic scale. |
Harmonic series (overtone chord or
scale). |
| a chord
(b, g, d
). |
a "inverted". |
| 1:2, 1:3, 1:5 models. |
Major-coloured third chords framed
by fifths. |
| Equidistant patterns: |
Chords made up of fifths, |
| whole-tone
scales, |
augmented triads (made from major thirds). |
| diminished
sevenths, |
|
| fourth chords, |
|
| augmented
triads |
|
| (made from
minor sixths). |
|
11)
The leading motive (bs. 2-5) of movement I is of this type.
12)
The chromatic fugue subject (its characteristic interval the minor third)
of Music for Strings, Percussion and Celesta acquires a diatonic shape
(its characteristic interval the fourth) in the final movement. The same
can be seen in the Divertimento movement III and Microcosmos No.64 "Line
and Point", versions a) and b):

13)
Which in fact results from the law of the golden section.
14)
The latter a-bb-d#-e
model can be broken down into the fifth a-e and the fourth bb-d#,
i.e. into the tonalities of a and d#; both are the Bartókian dominant
of the tonic F.
15)
Two intertonal minor third models can be so combined that they produce
the complete chromatic scale e.g. d-f-f#-a-bb-c#
+ e-g-g#-b-c-eb.
Equivalent to the intertonal minor third model scale is the g-type
chord structure below (5:3:5:3:5:3):

This chord structure will
be called g+g in this analysis. The 1:3 model can be constructed not only from three
minor thirds, but also three fourths, e.g. a-d + c#-f# + f-bb.
In the piano pieces "A bit Tipsy" and "See-saw", the 1:3 model arises as
a synthesis of e minor + Ab
major: e-g-b + c-eb-ab
= c-eb-e-g-ab-b.
16)
On the basis of the 1:2 model, it is possible to straightaway examine the
different intervals regarding their tonal significance. The interval root
of the major second, perfect fourth, minor sixth and major seventh is always
the upper note, that of the minor second, major third, perfect fifth and
minor seventh the lower note. In the case of the minor third, augmented
fourth and major sixth both lower and upper notes can be considered the
interval root, since they lie on the same axis.
17)
The reader will find an interesting example of the fact that the pentatonic
scale and the a
chord are related, the one easily being transformed into the other, in
the choral piece Senkim a világon (I’ve no one in the world). At
the repeat of the line "csendes folyóvíznek csak zúgását
hallom" (”I can hear only the soft murmur of the river below”; translated
by Miklós Hernádi) the pentatonic scale (db-bb-ab-f)
is projected into the d
chord (ab-f-d-c-a).
NEXT
Contents
|