|
Group Theory and Architecture 1: Nested Symmetries .
Professor Michael Leyton. Dept. of Psychology, Rutgers University Introduction In a forthcoming book, I give a comprehensive theory of design based on group theory. Whereas the book itself requires an advanced knowledge of group theory, the present series of articles will give the material in an intuitive form, and build up any needed group theory, in tutorial passages. The articles will begin by assuming that the reader has no knowledge of group theory, and we will progressively add more and more group theory in an easy form, until we finally are able to get to quite difficult topics in tensor algebras, and give a group-theoretic analysis of complex buildings such as those of Peter Eisenman, Zaha Hadid, Frank Gehry, Coop Himmelblau, Rem Koolhaas, Daniel Libeskind, Greg Lynn, and Bernard Tschumi. This first article is on a subject of considerable psychological relevance: nested symmetries. Nested Symmetries in Architecture Over the past 20 years, I have been showing, in my published research, that the human perceptual system is organized as a nested hierarchy of symmetries. This can be demonstrated with many kinds of psychological data on shape perception as well as motion perception. The consequence of the fact that our perceptual systems are organized in this way, is that we structure the environment into nested hierarchies of symmetries. I have also argued that artists and composers exploit this fact in the organization of their works. The purpose of this article is to introduce the reader to the idea that symmetries in architecture are nested. Let us consider the following example. It is a colonnade in a cathedral: 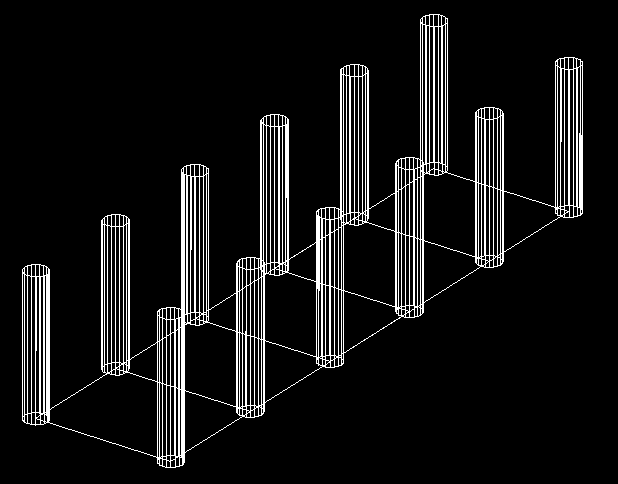
What we will do is build up this structure as a nested hierarchy of symmetries. We will proceed as follows: We start at the lowest level of the organization, which is actually a Point. Thus, take a point, and apply to it Rotations in the horizontal plane, to generate a circle. This circle is shown on the far left of the following figure:
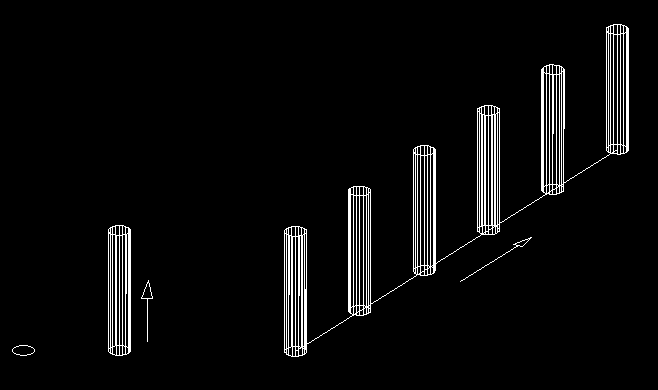
The circle represents the cross-section of the cylinder. Now take the generated circle, and apply to it translations in the vertical direction, which we will denote by TranslationsV. We will get the column, as shown in the second stage in the above figure. The vertical arrow shows the direction of the translations applied to the preceding circle. We next take this column and apply to it TranslationsH along a line in the horizontal plane as shown on the right in the above figure. This generates a row of columns, as shown in that figure. Finally, we take the row of columns and apply to it Reflections about a mirror-plane which is parallel to the column-row, and we obtain the reflectional pair of column-rows shown in the top figure on this page, i.e., the entire colonnade. The sequence of operations that were used can be represented as follows: where, reading from left to right, we started with a point, then applied rotations to get a column cross-section, then applied vertical translations to get a column, then applied horizontal translations to get a row of columns, and finally applied reflections to get the reflectional pair of column-rows. The important thing to notice is that these operations were nested. By this I mean the following: Each set of operations generates a level in the architecture. The levels are:
Furthermore, each level of transformations acted on the previous level as a whole. This is easy to see as follows: The point was acted on as a whole by Rotations to produce a circular cross-section; then the circular cross-section was acted on as a whole by TranslationsV to produce a column; then the column was acted on as a whole by TranslationsH to produce a row of columns; and finally the row of columns was acted on as a whole by Reflections to produce the reflectional pair of column-rows. Each level of transformations defines a symmetry in the architectural structure; i.e., point symmetry, rotational symmetry, translational symmetry, etc. Each level is, in fact, what is called a symmetry group in mathematics. In my research papers, I call this type of structure, a hierarchy of nested control. What I have shown is that the human perceptual system is organized as a hierarchy of nested control. In fact, the first research article I ever published was called "Perceptual organization as nested control." The perceptual system takes its nested structure and imposes it on the environment. What I argue is that architects exploit this psychological fact in the structure of their buildings. But the same is true of painters, and of composers. Now you might object by saying that the architectural example given above (the colonnade) is a highly regular structure, and therefore amenable to the type of analysis I have given. In contrast, you might ask, how can one describe the new types of architecture that are currently emerging, which involve irregular-shaped blocks (e.g., I.M. Pei's extension to the National Museum in Washington), and also free-form shapes (e.g., Frank Gehry's Guggenheim Museum at Bilbao)? In fact, it was exactly to analyze irregularity and free-form structures that I developed the concept of nested control. What I have shown is that, given an asymmetric design, the human perceptual system embeds this in a higher dimensional space in which it is described as a nested hierarchy of symmetries. The following is an illustration. In a sequence of psychological experiments, I conducted in the 1980's, I showed that, if people are presented with a rotated parallelogram (far left in the next figure), they then reference it to a non-rotated one, which they then reference to a rectangle, which they then reference to a square: Thus:
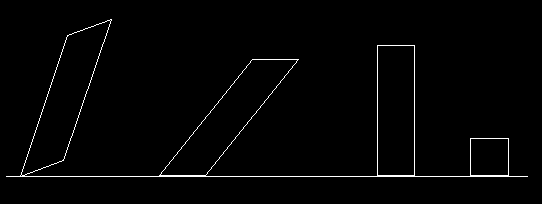
This means that they are actually describing a rotated parallelogram as generated in the following way. One starts with a square (far right). One applies to it a stretch to get a rectangle; then one applies to it a shear to get a parallelogram; and finally one applies to it a rotation to get a rotated parallelogram. This sequence is given thus: Each level is, once again, an example of what mathematicians call a symmetry group. Each is in fact a symmetry of some higher-order space of shapes. Now we have said that this sequence of operations is applied to a square. However, the square itself is built up as a nested hierarchy of operations. We start with an individual Point. We then apply to it Translations, to generate a side; and finally we take the side and apply to it the four 90oRotations to get a square. That is, the square is described as the following nested hierarchy of symmetries: Now, we said that the rotated parallelogram is obtained from the square by then applying Stretches to get a rectangle; Shears to get a parallelogram; and finally Rotations to get a rotated parallelogram. So the entire generative sequence, starting with a point, is this: The first three operations produce the square successively from a point, and then the next three operations produces the rotated parallelogram successively from a square. It turns out that this 6-level structure is a hierarchy of nested symmetries. Each level is a symmetry of some space, and the spaces are nested in each other. This 6-level nested hierarchy of control is a very powerful structure in the human perceptual system. I have shown for example, that it structures not only geometrical figures, such as those given above, but also motion phenomena. Now, we can go on adding higher levels of operations which will make the shape more and more asymmetric. As an example, I invented and published a free-form grammar which alters the curvature of the shape, so that it takes on more and more of an organic growth appearance. The grammar exactly analyzes Gehry's Guggenheim museum. Let me tell you where you can read more about this: The easiest, most accessible, description of this work is my 630 page book in MIT Press called "Symmetry, Causality, Mind". This is packed with examples showing how the human mind structures the environment in terms of nested hierarchies of symmetries. The first two chapters of the book give the free-form grammar that I just mentioned. Included in the book is also a 100 page chapter applying the free-form grammar to analyzing actual artworks in detail. The useful thing about this book is that everything is explained intuitively as I have done above. In contrast, all the technical mathematics will appear in a book that is nearing completion, and will be available within a year. To obtain my intuitive book in MIT Press, the reader can click: Symmetry, Causality, Mind. MIT Press, paperback Michael Leyton is president of the following two societies : International Society for Mathematical Aesthetics International Society for Group Theory in Cognitive Science
Home Page and email address: MLeyton@msn.com |