|
Why Symmetry? Why Asymmetry? by Michael Leyton, Page 2. To go back to: Page 1
The PISA Symmetry Analysis As we have seen, an essential aspect of the inference of history is symmetry. For a simple shape, a symmetry axis is usually defined to be a straight line along which a mirror will reflect one half of the figure onto the other. However, observe that, in complex natural objects, such as the branch of a tree, a straight axis might not exist. Nevertheless, one might still wish to regard the object, or part of it, as symmetrical about some curved axis. For example, a branch of a tree tends not to have a straight reflectional axis. Nevertheless, one understands the branch to have an axial core that runs along its center. How can such a generalized axis be constructed? There are good mathematical reasons to proceed in the following way. Consider the next figure. It shows two curves c1 and c2 (the bold curves), which can be understood as two sides of an object. We will construct a symmetry axis between the two curves. In fact, the axis, we will produce, will be indicated by the sequence of dots shown. It is produced in the following way: Introduce a circle that is tangential simultaneously to the two curves, as shown. The two tangent points A and B are then defined as symmetrical to each other. 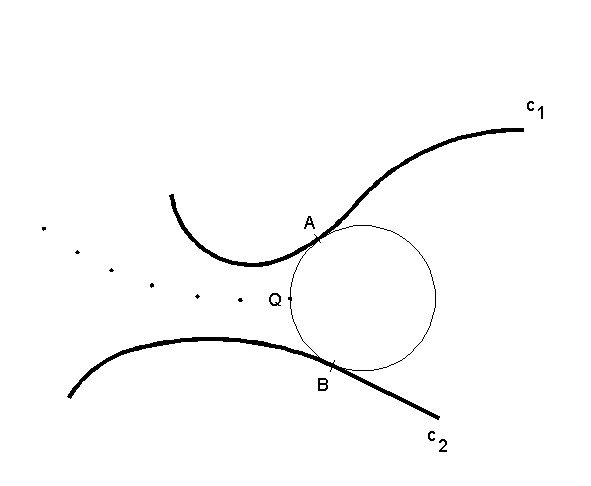 Then move the circle continuously along the two curves, c1 and c2, while always maintaining the property that it is simultaneously tangential to the two curves. One might need to expand or contract the circle to maintain the double-touching property. Now define the symmetry axis to be the trajectory of the midpoint Q of the arc AB, as the circle moves. For example, in the above figure, the trajectory of Q is represented by the locus of dots shown. This definition of symmetry was proposed by me in Leyton (1988), where I argued that it is more suited for the particular task of process-inference than are other symmetry analyses, such as those proposed by Blum and Brady. The intuitively satisfying results of our alternative analysis will be seen later. I called the above definition of symmetry axis, Process-Inferring Symmetry Axis, or simply PISA .
Symmetry-Curvature Duality The Free-Form Grammar relies on two structural factors in a shape: symmetry and curvature. Mathematically, symmetry and curvature are two very different descriptors of shape. However, a theorem that I proposed and proved in Leyton (1987b) shows that there is an intimate relationship between these two descriptors. This relationship will be the basis of the entire paper: SYMMETRY-CURVATURE DUALITY THEOREM (Leyton, 1987b): Any section of curve, that has one and only one curvature extremum, has one and only one symmetry axis. This axis is forced to terminate at the extremum itself. To illustrate: Consider the shape shown in the following figure. The section of curve between the two letters m, has only one curvature extremum - that indicated by the letter M. The theorem says that this section of curve can have only one symmetry axis, and that the axis is forced to terminate at the extremum. 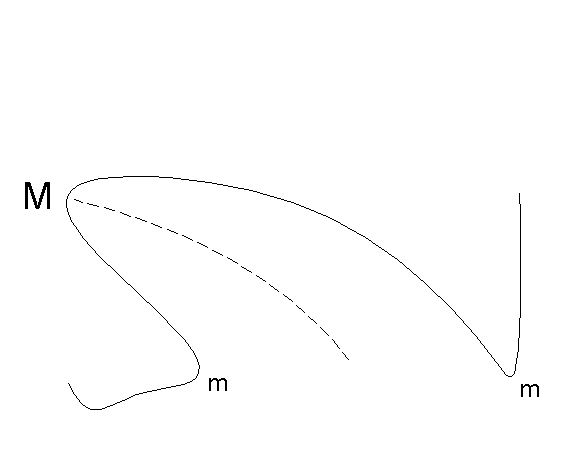
Symmetry Axes and Processes The reason for involving symmetry axes is that it will be argued that they are closely related to process-histories. This proposed relationship is given by the following principle: INTERACTION PRINCIPLE (Leyton, 1984): The symmetry axes of a perceptual organization are interpreted as the directions along which processes are most likely to act or have acted. The principle was advanced and extensively corroborated in Leyton (1984, 1985, 1986a, 1986b, 1986c, 1987a, 1987b, 1987c), in several areas of perception including motion perception as well as shape perception. The argument used in Leyton (1984, 1986b), to justify the principle, involves the following two steps: (1) A process that acts along a symmetry axis tends to preserve the symmetry; i.e. to be structure-preserving. (2) Structure-preserving processes are perceived as the most likely processes to occur or to have occurred.
The Inference of Processes We now have the tools required to understand how processes are recovered from shape. In fact, the system to be proposed consists of two inference rules that are applied successively to a shape. The rules can be illustrated considering the following figure: 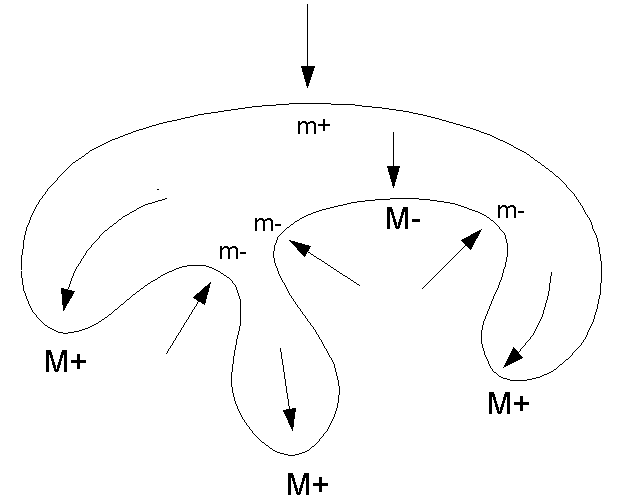 The first rule is the Symmetry-Curvature Duality Theorem which states that, to each curvature extremum, there is a unique symmetry axis terminating at that extremum. The second rule is the Interaction Principle, which states that each of the axes is a direction along which a process has acted. The implication is that the boundary was deformed along the axes; e.g. each protrusion was the result of pushing out along its axis, and each indentation was the result of pushing in along its axis. In fact, each axis is the trace or record of boundary-movement! (The vertical arrow at the top is a squashing and the rules for inferring this are the same, as we shall see later.) Under this analysis, processes are understood as creating the curvature extrema; e.g. the processes introduce protrusions and indentations etc., into the shape boundary. This means that, if one were to go backwards in time, undoing all the inferred processes, one would eventually remove all the extrema. Observe that there is only one closed curve without extrema: the circle. Thus the implication is that the ultimate starting shape must have been a circle, and this was deformed under various processes each of which produced an extremum.
To continue: NEXT PAGE
|