DECORATIONS BY MEANS OF GENERALIZED CLOTHOIDS

G. Lucca

(Italy)

vanni_lucca@inwind.it

Abstract

The paper describes a method to create decorative figures based on curves that can be considered a generalization of the clothoid. Some examples of application are presented. 

1. Introduction

The clothoid, also known as Cornu spiral or Euler spiral, is a plane curve which is often applied in optics, for diffraction studies, and in the design of civil constructions, like roads and railway lines, when it is necessary to create a connection between a straight stretch and a bend. Its characteristics and main properties are described in many textbooks or web-sites (see for example [1], [2]). Its equation, expressed in cartesian parametric form by means of the Fresnel integrals, is: 

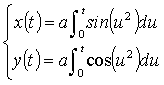                                                         (1)

An example, (with a=(2/p)^½), is plotted in Fig.1.  The parameter t in equations (1) (being -¥ < t < ¥) is strictly related to the arc length of the curve s (measured from the axes origin O) by means of the relation t = s/a.

Fig.1: Clothoid

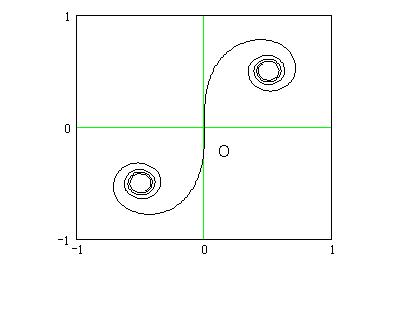
The property of having the curvature proportional to the arc lengthis the main characteristic of the clothoid. 

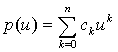2. Generalized clothoids

The argument of the sine and cosine functions in equations (1) can be generalized (see [2]) to a generic polynomial p(u) of n degree and characterized by coefficients c_k (k=0,1, ..,n) expressed by means of the following relation:

                                                             (2)

In such a way, equations(1) are generalized into:

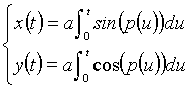                                                             (3)

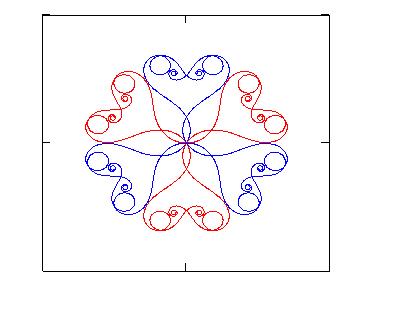
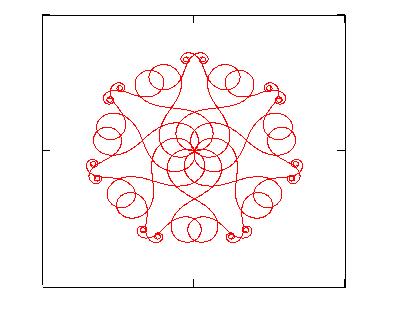
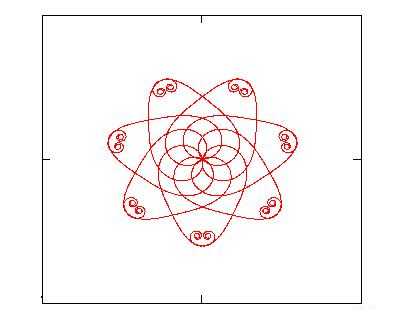
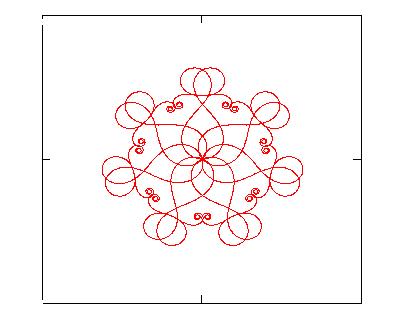
Figs.2a, 2b, 2c show some examples of curves that can be plotted starting from equations (3). The characteristic of these curves of being at the same time curly and symmetrical makes them suitable to design some decorations that we are going to present in the next paragraph.

Figs.2a,2b, 2c: Examples of generalized clothoids

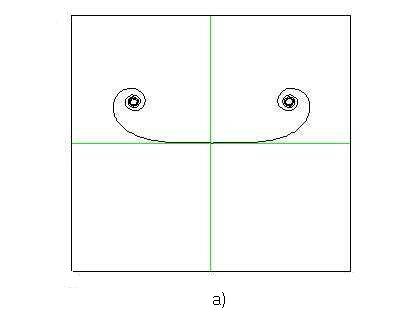
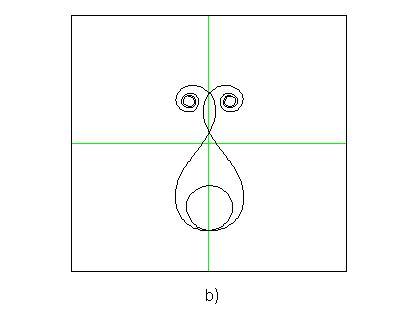
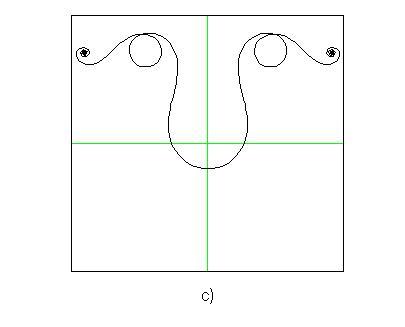
It is interesting to note that curves similar to the ones shown in Fig.2 can quite often be found as decorations in metal gates, barred windows and fences.

It is worthwhile to mention that also different functions from polynomials can be used to obtain generalized clothoids; thus, being f(u) a continuous function together with its first derivative, we can write:

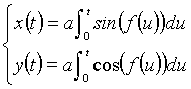                                               (4)

Related to this point, we just would like to mention that the artist J. P. Hébert, created some art-works by drawing in the sand, by means of a special installation, some curves that can be considered generalized clothoids according to the equations (4). (See [3] for more details).

Finally, it can be shown that the curvature k(u) of the generalized clothoid is related to the function f(u) by means of the following relation:

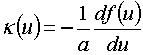                                                        (5)

In the following we shall consider, according to equations (3), only polynomials.

3. Creating decorations

Three are the steps which can be followed in order to create decorative figures starting from generalized clothoids:

choose one basis curve described by equation (3); the shape of the curve is related to the degree n of the polynomial p(u) in equation (2) as well as to the value of the coefficients c_k appearing in it; we shall name it mother curve;

generate any number N-1 of daughter curves by applying to the mother curve the typical geometrical transformations like rotation, reflection, homothety;

plot together mother and daughter curves in order to obtain the decoration.

Clearly the choice of the mother curve and of the number of daughter curves, as well as their disposition, is up to the personal aesthetic taste in looking at the final result obtained.

4. Examples

In this paragraph some decorative figures are shown (see from Fig.3 to Fig.12); in all the following examples, we have derived N-1 daughter curves from the mother curve by simply rotating it, with respect to the origin, of  an angle f_j= j2p/N (j=1,2,..N-1); in such a way, figures with many axis of symmetry are obtained; some of them recall shapes like flowers, stars, crosses. The details about the formulas and the data used for generating the figures are given in the Appendix.

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Fig.9

Fig.10

Fig.11

Fig.12

5. Conclusions

The paper has presented a method for creating some decorative figures by using a generalization of the curve usually known as clothoid or Cornu spiral; some examples have been shown.

APPENDIX

All the data used to generate the figures shown in par.4 are reported in compact form in Table I; in the third column, N is the total number of curves (mother curve and N-1 daughter curves) used in order to get the figures; in the last column, [t_min ,t_max] is the interval chosen for the parameter t in order to draw the figures. As far as the parameter a present in formula (3) is concerned, it has been considered equal to 1. 

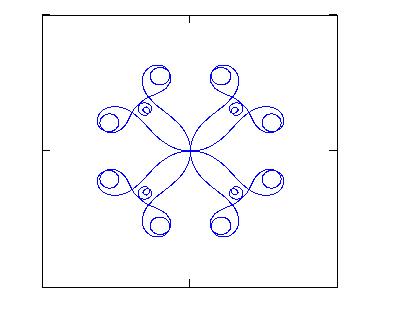
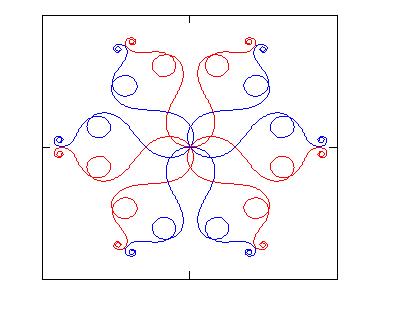
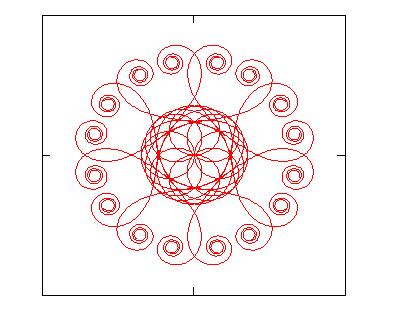
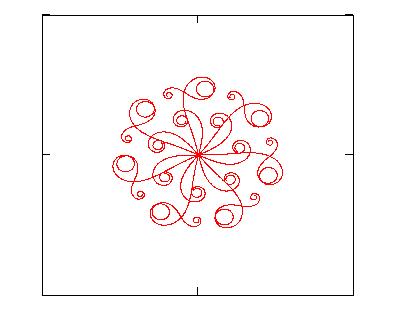
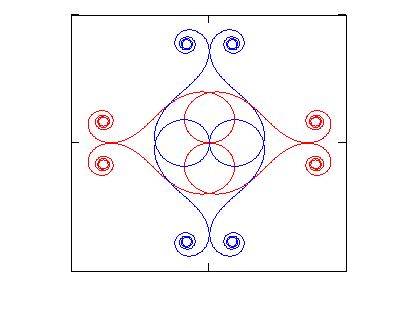
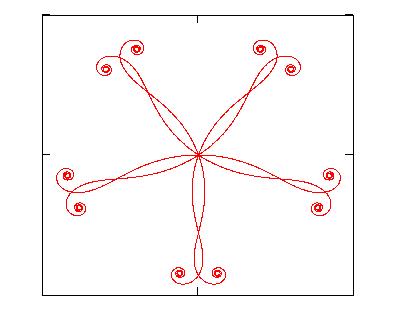
Fig.	p(u)	N	[tmin, tmax]
3	u^5-6.1u^3+3.1u	4	[-2.262, 2.262]
4	u^5-6.u^3+5.4u	6	[-2.356, 2.356]
5	0.333u^3-4u	8	[-4.712, 4.712]
6	u^5-6u^3+4.32u	7	[-2.356, 2.356]
7	u^5-6u^3+7u	7	[-2.356, 2.356]
8	2.4u^5-6u^3+7u	7	[-1.728, 1.728]
9	2.4u^5-9.3u^3+6.7u	7	[-1.948, 1.948]
10	2u^5-10.5u^3+4u^2	7	[-1.005, 2.042]
11	0.333u^3-3.275u	4	[-4.712, 4.712]
12	u^5-u	5	[-1.885, 1.885]

Table I: Data used for generating the figures shown in the paper.

References

[1]http://www.mathcurve.com/courbes2d/cornu/cornu.shtml

[2]http://mathworld.wolfram.com/CornuSpiral.html

[3]http://www.mathematica-journal.com/issue/v7i3/graphics/