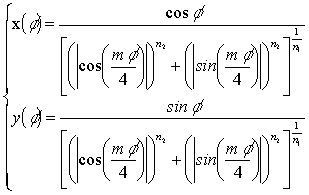 (1)
(1)MODELLING STARFISHES SURFACE
G. Lucca
(Italy)
Abstract: The paper describes a model able to represent starfishes surface in parametric form by means of simple analytical expressions. Some examples of imaginary starfish shapes are presented.
1. INTRODUCTION
Since ancient times, starfishes (also named sea stars) have always fascinated human kind for their beauty and their striking shape based, in most of cases, on penta-radial symmetry; nevertheless starfishes having a different number of arms (e.g. 4, 6, 11, 24), and thus a different degree of symmetry, exist too [1], [2].
The main purpose of this work, is to visually represent the basic features of their shape by proposing an algorithm able to generate some geometrical objects which have to be intended just as abstract and simplified models of real world starfishes.
The paper is organized according to the following steps:
description of the formula for generating the starfish curve in the plane;
description of the formula for generating the starfish surface;
modelling bumps;
presentation of some examples.
2. STARFISH CURVE IN THE PLANE
The starting point is to represent the starfish curve in the x-y plane; a fruitful technique is to use the so called Superformula proposed by J. Gielis [3], [4], [5]; it consists in a simple analytical expression which allows to draw a very large variety of plane curves just by choosing suitable values relevant to few parameters.
For our purposes, the formula able to analytically draw the star shape in polar coordinates with respect to the polar angle f (with fÎ[0, 2p]) is:
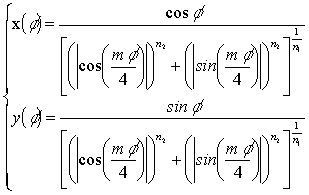 (1)
(1)
In formula (1) m is an integer number related to the numbers of arms of the star ( typically m=5), n1and n2 are real positive number which characterize the shape of the star (length and width of the arms).
One can verify that for (n1/n2) > 1 the star has practically no arms while, for decreasing values of the ratio n1/n2 (provided that n1/n2 < 1) together increasing values of n2, the star has more and more a slender shape (i.e. long and thin arms).
3. BASIC EQUATION OF THE STARFISH SURFACE
The starfish surface can be obtained by simply traslating the star curve drawn in the x-y plane along the z vertical axis and, at the same time, by applying an homothety with respect to x and y axes according to a certain law that we are going to specify.
Such a law has to describe the vertical profile of the starfish surface; if we define by D the distance between ''south pole'' (z=0) and ''north pole'' (z=D), a suitable and simple function f(z) able to describe the starfish slope in interval [0, D] is:
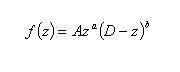 (2)
(2)
being A, D, a, b positive real numbers.
By suitably choosing the above parameters one can design many kinds of profiles with different slopes; in particular a and b control the profile shape while A its elongation.
For the following, it is useful to add that the profile has the maximum value for zmax=aD/(a+b).
As mentioned before, the translation of the star curve along the z axis in the interval [0, D] together the homothety with respect to x and y axes is able to generate the starfish surface; such a surface is expressed in parametric form with respect to the independent variables f and z by means of the following equations:
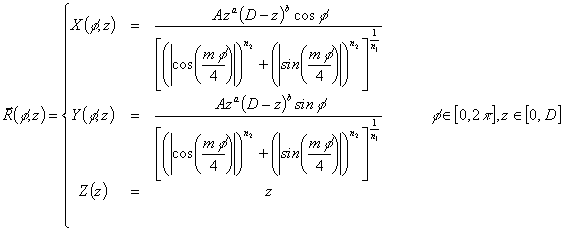 (3)
(3)
Formula (3) is then a seven parameters formula (i. e., m, n1, n2, A, D, a, b) able to describe a very wide range of starfish shapes.
The above parameters completely determine the starfish shape; nevertheless, it may be useful to relate the surface shape to more intuitive parameters; to this aim, we can also introduce some ancillary dimensionless parameters which have to be considered just an help in designing the starfish shape. First of all we need to definine the following quantities:
dmax: distance from the tips of one of the arms to the z-axis (i.e. maximum horizontal distance evaluated on the plane z=zmax);
dmin: distance from the notches between two arms to the z-axis (i.e. minimum horizontal distance evaluated on the plane z=zmax).
In such a way, we may introduce the following ancillary parameters:
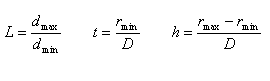 (4)
(4)
In particular:
L (L>1) is related to the slenderness degree of the shape in the horizontal plane i.e. as L increases the star has longer and longer arms with respect to central body;
t is related to the flatness degree of the starfish central body radius;
h is related to the flatness degree of the starfish arms.
4. MODELLING BUMPS AND SPIKES
We would like to remark that the system of equations (3) allows to model the basic shape of a starfish surface; nevertheless, in many cases, starfish surfaces are characterized by the presence of bumps and spikes on it. To this aim, a way to model these kinds of ornamentations is to add to the basic smooth surface, described by equation (3), a certain number of localized perturbations each one applied in points belonging to the surface and having its center at given coordinates (fk , zk). (Being k=1, 2, ..,N and N the number of bumps)
The generic k-th bump can be represented by means of a vectorial bell-shaped function Pk described by the following formula:
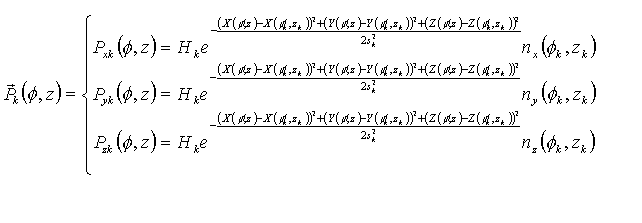
(5)
In formula (5), Hk and sk are amplitude and width of the k-th bump respectively while nx(fk, zk), ny(fk, zk) and nz(fk, zk) are the components of the normal to the smooth surface evaluated at (fk , zk).
It is useful to remind that, in our case, the equation of the normal is given by [6]:
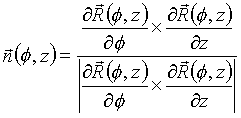 (6)
(6)
Therefore by adding (3) and (5), the equation of the surface with bumps is represented by the following equation in vectorial form:
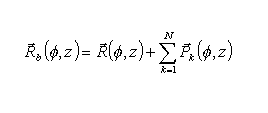 (7)
(7)
Thus, in order to summarize, the parameters characterizing the generic k-th bump are: coordinates center (fk , zk), height Hk and width sk.
5. EXAMPLES
In this paragraph we show some examples of different starfish shapes that can be obtained by applying the formulas presented in the previous paragraphs. The examples represent just some imaginary starfishes, but our opinion is that the model is able to catch the basic features of real starfishes provided that some input data are known from measurements on specimen; in such a way it would be possible to experimentally determine numerical values for the parameters influencing the surface shape.

Fig.1

Fig.2

Fig.3

Fig.4
Fig.5

Fig.6

Fig.7

Fig.8

Fig.9

Fig.10
6. CONCLUSIONS
In this paper we have proposed a method for describing, in analytical way by means of simple formulas, the starfishes surface; moreover, the model presented is also able to describe the presence of bumps or spikes on the surface itself. Some examples of application relevant to imaginary starfishes are shown.
REFERENCES
http://www.enature.com/search/show_search_byShape.asp?curGroupID=8&shapeID=1072
http://dnr.metrokc.gov/wlr/waterres/beaches/seastar/seastarkey.htm
E. Kreyszig: ''Advanced Engineering Mathematics'', John Wiley & Sons, Inc., New York, Fourth Edition 1979, p. 432.