The recent generalizationsof colored symmetryLungu AlexandruState University of Moldova str. A. Mateevici 60 MD 2009 Chisinau Moldova lungu@usm.md
Abstract. In this article we analyze the essence of the recent "physical'' generalizations of classical symmetry from the viewpoint of the split extensions of groups. The principal results of the general theory of groups of Wp- and Wq-symmetry are given. The methods of deriving generalized symmetry groups of different types are formulated. All these methods are based on right, left and crossed quasi-homomorphisms and their generalizations. The principal properties of diverse quasi-homomorphic mappings are examined. The article is illustrated with many examples of colored and ïndexed" geometrical figures that are described by the groups of P-,`P-, Wp- or Wq-symmetry. Keywords: color symmetry groups; W-symmetry
groups; action of automorphism; generalizations of homomorphism; quasi-homomorphic
reflections; wreath products.
AMS Subject Classification: Primary: 20H15; 20E36; 20B25; 20A05; 51M20; 51N30; Secondary: 52; 82.
1. Introduction It is well known that the modern theory of symmetry of the real crystal gives rise to new generalizations. One of the essential generalizations of classical symmetry is the P-symmetry of A.M.Zamorzaev [1-3]. In the case of P-symmetry, the transformations of the qualities attributed to the points, are combined directly with the geometrical transformations and do not depend on the choice of points. Other proposed generalizations such as polychromatic symmetry of Wittke-Garrido [4] or complex [5] symmetry are not included in the scheme of A.M.Zamorzaev's P-symmetry. For these generalizations, the transformations of the qualities attributed to the points, essentially depend on the choice of points. The mentioned generalizations are included in Wp-symmetry that was introduced by V.A.Koptsik and I.N.Kotsev [6] and was developed in the cycle of papers [3, 6-21, 28, 33, 35]. On the other hand, V.A.Koptsik in [22] proposed the notion of Q-symmetry. The essence of Q-symmetry consists actually in the following: the transformation of Q-symmetry g(q) is composed from the components g and q, where g is transformation of symmetry which operates both on points (the atoms of crystal) and on indexes (vector or tensor) by the given rule independent of the points, and q is a supplementary transformation of these indexes. Uniting problems to be solved for Wp-symmetry and Q-symmetry (`P-symmetry [23-25]), we shall get a generalization named Wq-symmetry [26-33]. The methods of deriving the groups of P-symmetry
of different types [1, 2] are based
on homomorphic mapping and its properties. The solution of analogous problems
for`P]-
and W-symmetry demands the generalization of homomorphisms as the
right quasi-homomorphism [23, 3],
the natural left quasi-homomorphism [14], and the
crossed quasi-homomorphism [27]. Moreover, it requires
the investigation of some their properties.
2. The crossed standard Cartesian wreath product of groups Let us have groups G and P. Construct the
Cartesian product W of isomorphic copies of the group P which
are indexed by elements of G: W =`Õgi
Î
GPgi,
where Pgi
@ P.
Moreover, construct the isomorphic injection f:
G®Aut
W by the rule f(g) = If W is a direct product of the isomorphic copies
of the group P which are indexed by elements of G, then at
analogous mode it defined the crossed standard direct wreath product
of groups P and G.
3. The essence of the recent generalizations of color symmetry Ascribe to each point of a geometrical figure F with the discrete symmetry group G at least one index, which means a non-geometrical feature, from the set N = {1,2,...,m}, and fix a certain transitive group P of the permutations of these indexes. The transformation of P-symmetry is defined to
be an isometric mapping g(p) = gp = pg
of the "indexed" geometrical figure F(N) onto
itself in which the geometrical component g operates only on points,
and the indexes are transformed by the permutation p of the group
P.
The set G(P) of transformations of P-symmetry
of any "indexed'' geometrical figure F(N) forms
a group with the operation
where gk = gi gj and pk = pi pj [1]. The groups G(P) of P-symmetry are subgroups of the direct products of the group P of permutations with their generating discrete groups G of classical symmetry. Example 1. Let F be a geometrical figure
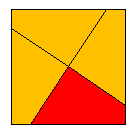
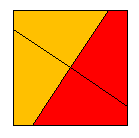
with the classical symmetry group G = 4 = (1, 4, 2, 4-1)
(we use Shubnikov's symbols [34]) and N = {
1,2,3,4 }, where the yellow, green, red and blue colors are denoted with
the indexes 1,2,3 and 4, respectively. Moreover, P = (e,
p1
= (1234), p2 = (13)(24), p3 = (1432)).
Then g(p) = gp = 4p1
is a transformation of P-symmetry of the colored square represented
in Figure 1.
Figure 1 The group of above P-symmetry is
with the group/subgroup symbol 4/1, where 4 is the symbol of the generating group and 1 is the symbol of its classical symmetry subgroup [2]. The transformation of `P-symmetry is defined to be an isometric mapping g(p) = pg of the "indexed'' geometrical figure F(N) onto itself in which the geometrical component g operates both on points and on indexes by the given rule independent of the points, but the permutation p is only a compensating permutation of indexes to map F(N) onto itself and p Î P. In this case the components p and g of the transformation g(p) in general do not commute: pg ¹gp, that is why p ¹ gpg-1. The set G(`P) of transformations of `P-symmetry of any "indexed'' geometrical figure F(N) forms a group with the operation
Example 2. Let us have six different positions
of vectors with the equal modules, that are numbered using 1,2,3,4,5 and
6 in accordance with the scheme represented in Figure 2.
Figure 2 In this case, the "ïndexed" figures represented in
Figure 3a) and Figure 3b) are described from the viewpoint of P-symmetry
by the same group with the group/subgroup symbol 4/1.
Figure 3 From the viewpoint of `P-symmetry the "ïndexed" figures represented in Figures 3a) and 3b) are described by the different groups [3]. Construct the Cartesian product W of isomorphic
copies of the group P which are indexed by elements of G,
i.e. W = `ÕgiÎ
GPgi,
where Pgi
@ P.
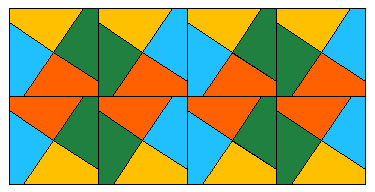
Example 3. Let's have the groups G = 4 and P = (e, p = (12)), where the yellow and red colors are denoted with indexes 1 and 2. Then g(w) = gw = 4 < p1, e4, p2, e4-1> is a transformation of Wp-symmetry of the colored square represented in Figure 4.
Figure 4 We note that in the case when G = 4 and P = (e, p = (12)), the transformation of Wp-symmetry g(w) = 4 < p1, p4, p2, p4-1> exists too, which may be formally considered as a transformation of P-symmetry (it satisfies the conditions of the respective definition - there is one rule of the transformation of colors for all equivalent points) [35]. This transformation and the transformation of P-symmetry g(p) = gp = 4p describe the same colored square (Figure 5).
Figure 5 The groups G(Wp) of Wp-symmetry are subgroups of the left standard Cartesian wreath product of the initial group P of permutations with the discrete group G of classical symmetry as their generating group:
The transformation of Wq-symmetry is defined to be an isometric mapping g(w) = wg of the "indexed'' geometrical figure F(N) onto itself in which the geometrical component g operates both on points Mk = gk(M1) of the figure F(N) (where M1 is a point of general position of the figure F with respect to the group G) and on indexes by the given rule independent of the points, but the permutation pgk ("gk-component'' in w) is only a compensating permutation of indexes in the point Mk to map F(N) onto itself. The set G(Wq) of transformations of Wq-symmetry of the given "indexed'' figure F(N) forms a group with the operation
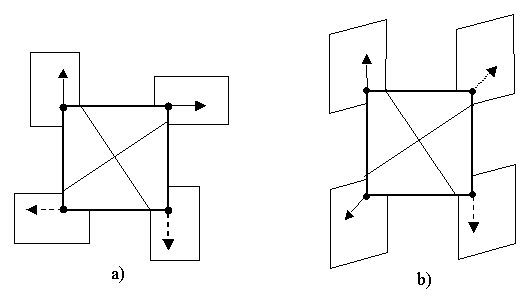
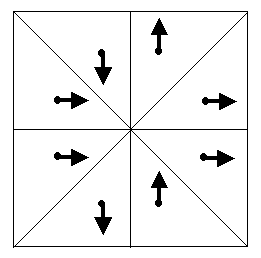
Example 4. Let us have four different positions
of vectors with the equal modules that are numbered using 1,2,3 and 4 in
accordance with the scheme that is represented in Figure 6;
Figure 6 let's have the groups G = C4 = 4 = (1, 4, 2, 4-1) and P = (e, p1 = (1234), p2 = (13)(24), p3 = (1432)) @C4. Then g(w) = wg = < p11, p34, p12, p34-1> 4 is a transformation of Wq-symmetry of the "ïndexed" figure represented in Figure 7.
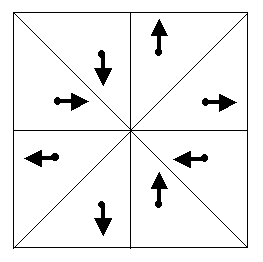
Figure 7 We note that in the case when G = C4v
= 4 ·m = (1, 4, 2, 4-1, m1,
m2,
m3,
m4)
and P@C4, the transformation
of
Wq-symmetry
g(w) = wg
= <
p21,
p24,
p22,
p24-1,
p2m1,
p2m2, p2m3,
p2m4 > 4
exists too, which may be considered formally as a transformation of `P-symmetry.
This transformation and the transformation of `P-symmetry
g(p)
= pg = p24 describe the same "ïndexed" figure
F(N)
represented in Figure 8.
Figure 8 The groups G(Wq) of
Wq-symmetry
are subgroups of the crossed standard Cartesian wreath product of the initial
group P of permutations and the discrete group G of classical
symmetry (as their generating group), accompanied with the homomorphism
t:
G®Aut
W by the rule t(gi) =
4. On the classification and the general structure of W-symmetry groups Let G(W) be a group of Wp-
or
Wq-symmetry with the initial group P, generating
group G and subset W¢
= {w | g(w)ÎG(W)}
ÍW.
Identifying the groups G and W with their isomorphic injections
into G The group G(W) is called senior, junior or V-middle if w0 < V = W¢ = W, w0 = V < W¢ = W or w0 < V < W¢ = W, respectively. If W¢ is a non-trivial subgroup of W, then the group G(W) is called W¢-semi-senior, W¢-semi-junior or (W¢, V)-semi-middle according to the cases when w0 < V = W¢, w0 = V < W¢ or w0 < V < W¢. If W¢ÌW, but W¢ is not a group, the group G(W) is called W¢-pseudo-junior or (W¢, V)-pseudo-middle when w0 = V Ì W¢ or w0 < V Ì W¢. Let G(Wp) be a group of Wp-symmetry with the initial group P, generating group G, subset W¢ = {w | g(w) ÎG(Wp)}, symmetry subgroup H and the subgroup V of W-identical transformations. Then: 1) the mapping f of the group G(Wp) onto the group G by the rule f[g(w)] = g is homomorphic with the kernel V; 2) the group
G(Wp)
contains as its subgroup the group G1(W1)
of P-symmetry (which is determined by initial group P of
permutations, where W1£ Diag
W @P and W1ÌW¢)
from the family with the generating group G1 (G1
£
G),
with the symmetry subgroup
H (where H Moreover, if W is a finite group then: 1) Vg = wVw-1, where g and w are components of the transformation g(w) from G(Wp); 2) all the elements of a right coset Hg of the group G by H are combined in pairs only with the elements of one left coset wV, and the elements of different cosets Hgi and Hgj with the elements of different cosets wiV and wjV [18-20, 28]. Let G(Wq) be a group of Wq-symmetry with the generating group G, permutation group P, (i.e. W = `Õgi Î GPgi, where Pgi @ P), subset W¢ = {w | g(w) Î G(Wq)}, with the kernel H1 of accompanying homomorphism t: G ® Aut W, symmetry subgroup H and the subgroup V of W-identical transformations. In this case the following conditions are satisfied: 1) the mapping f of the group G(Wq) onto the generating group G by the rule f[g(w)] = g is homomorphic with the kernel V; 2) the group G(Wq) contains as subgroup the group H1(Wp) of Wp-symmetry (which is determined by the initial group P of permutations) from the family with the generating group H1, with the symmetry subgroup H¢ (where H¢ = H Ç H1) and with the same subgroup V of W-identical transformations; 3) the group G(Wq) contains as a subgroup the group G1(W1) of `P-symmetry (which is determined by initial group P of permutations) from the family with the generating group G1 (where G1 £ G), with the same kernel H1 of the accompanying homomorphism and with the set W1 = {w | g(w) Î G1(W1)} of multi-component permutations, where W1 = W¢ Ç Diag W. If W is a finite group of multi-component permutations, then: 1) Vg
= V for any transformation g(w) from G(Wq),
i.e. V is 2) 5. On the right and left quasi-homomorphisms Let us have groups G and P and a homomorphism f: G®Aut P. The mapping y of the group G onto the subset P¢ of the group P by the rule y(g) = p is called a right quasi-homomorphism if for any gi and gj from G
At the right quasi-homomorphism y, in general, the image of G y(G) = P¢Ì P is not a group, but P¢ always contains the unit of the group P. The kernel H of the right quasi-homomorphism y of the group G into the group P is a subgroup in G; the index of this subgroup coincides with the power of y(G). The mapping
The necessary and sufficient condition for the mapping
6. On the methods for deriving groups of P- and `P-symmetry Any group G(P) of complete P-symmetry (P¢ = P) can be derived from its generating group G and permutation group P by the following steps: 1) to find in G and in P all invariant subgroups H and Q for which there is the isomorphism of factor-groups S/H and P/Q (l: G/H ® P/Q) by the rule l(gH) = pQ; 2) to combine pair-wise each g¢ of gH with each p¢ of pQ = l(gH); 3) to introduce into the set of all these pairs the operation (1). If Q = e (G(P)
is a junior group), then the isomorphism l:
G/H
®
P
is, in fact, a homomorphism of the group G onto
P (i.e. it
is a representation of the group
G) with the kernel
H [1,
2].
Example 5. In the case when the generating group
G
= {a, b} (4) (we use Zamorzaev's symbols [2])
and the permutation group P = (e, p1 =
(1234), p2 = (13)(24), p3 = (1432))
@
4, we have only three different junior groups of 4-symmetry. Their geometrical
interpretations are represented by colored periodical mosaics (Figures
9 - 11).
Figure 9: Geometrical interpretation of the junior
group {a, b} (4(4)).
Figure 10: Geometrical interpretation of the junior
group {a, b} (4(-4)).
Figure 11: Geometrical interpretation of the junior group {a(2), b(2)} (4(4)).
Any group of `P-symmetry (with a finite group P) can be derived from its generating group G, knowing the kernel H of accompanying homomorphism f: G ® Aut P, by the following steps: 1) to find
in P all subgroups Q and subsets P¢,
which are decomposed in right cosets by its subgroup Q, and in G
all proper subgroups H¢
(H¢<
G) with
the index equal to the power of set of all the right cosets of P¢by
Q and for which there is the isomorphism l
of factor-groups H/H¢¢
and P¢¢/Q (l:
H/H¢¢
® P¢¢/Q)
by the rule l(gH¢¢)
= pQ) where e 2) to construct
a generalized right quasi-homomorphism 3) to combine
pair-wise each g¢ of
gH¢
with each p¢ of Qp
=
4) to introduce into the set of all these pairs the operation (2). If Q = e, then the mapping 7. On the generalized exact natural left quasi-homomorphisms and the groups of Wp-symmetry The natural left quasi-homomorphism m
of the group G into the group W = `Õgi
Î
GPgi
under which the automorphism
The necessary and sufficient condition for the mapping
m
of the group G onto the subset W¢
of the group W = `Õgi
Î
GPgi
by the rule m(g) = w to be an
exact natural left quasi-homomorphism is that (wi) 1) G/H @ W¢), 2) W¢ Let us have the group G, the finite group W
= Õgi Î
GPgi,
its subgroup V (V < W)
and the exact isomorphic injection f of the
group G into the subgroup
The necessary and sufficient condition for the mapping
If V Any group G(Wp) of Wp-symmetry with the finite group W can be derived from its finite generating group G and a group W = Õgi Î GPgi of multi-component permutations by the following steps: 1) to find in W all subgroups V and subsets W¢, which are decomposed in left cosets by its subgroup V, and in G all proper subgroups H with the index equal to the power of set of all left cosets of W¢ by V and for which there is the isomorphism l of factor-groups G1/H and W1/V1 (l: G1/H ® W1/V by the rule l(Hg) = wV), where G1£ G, W1 £ Diag W and V1 = V Ç Diag W £ W1; 2) to construct
a generalized exact natural left quasi-homomorphism 3) to combine
pair-wise each g¢ of
Hg
with each w¢ of wV
= 4) to introduce into the set of all these pairs the operation (3) [16-21, 28]. If V = w0, where w0
is the unit of the group W, then the mapping For the groups G(Wp) of Wp-symmetry the polynomial symbol (the symbol is formed from more terms) was proposed in the form
1) G is the generating group for G(Wp); 2) P is the initial group of permutations; 3) W¢ = {w| g(w)Î G(Wp)} Í W; 4) V is the subgroup of W-identical transformations; 5) H is the classical symmetry subgroup; 6) G1/H¢/H is the trinomial symbol (the three-term symbol) for the group of P-symmetry G1(W1) in accordance with [34, 2]; 7) W1 / V1 @ G1/H, where V1 = V Ç Diag W £ W1 and W1 = W¢Ç Diag W. In the case of semi-junior and pseudo-junior groups the polynomial symbol becomes simpler and takes the form
Example 6. The colored square represented in Figure 4 is described by the semi-junior group of Wp-symmetry G(Wp) = (1w0, 4w1, 2w2, 4-1w3), where w0 = < e1, e4, e2, e4-1> is unit of the group W = P1 × P4 × P2 × P4-1 with P = (e, p = (12)), w1 = < p1, e4, p2, e4-1>, w2 = < p1, p4, p2, p4-1> and w3 = < e1, p4, e2, p4-1> . The polynomial abbreviated symbol of this group has the form 4/(2/1/1). We note that the colored square represented in Figure 5 is described by the semi-junior group of Wp-symmetry G1(Wp) = (1w0, 4w, 2w0, 4-1w), where w = < p1, p4, p2, p4-1> ; the polynomial abbreviated symbol of this group has the form 4/(4/2/2). Moreover, the same colored square is described by the junior group of P-symmetry G(P) = (1e, 4p, 2e, 4-1p), with the three-term symbol 4/2/2. The group G1(Wp) may be formally considered as a group of P-symmetry. The square with classical symmetry group G = C4 may be painted with two colors by one more mode [35] (Figure 12).
Figure 12: Geometrical interpretation of the pseudo-junior
group
8. The crossed quasi-homomorphisms and the semi-junior groups of Wq-symmetry Let us have groups G, P and W = `Õgi
Î
GPgi
(where Pgi
@ P),
the isomorphic injection f:
G ®
Aut
W by the rule f(g) =
We note that in the case of In general, the image of G, a(G) = W¢Ì W is not a group, but W¢ always contains the unit of the group W. The kernel H of crossed quasi-homomorphism a of the group G in the group W is a subgroup of the group G. Let us have crossed quasi-homomorphism a with Ker a = H of the group G onto the subset W¢ of the group W accompanied by exact left translations of components and by the homomorphism t of right conjugation with Ker t = H1. Then: 1) the necessary and sufficient condition for the mapping a to send each left coset gH onto the only element w is that wh = w for any h Î H = Ker a and w ÎW¢; 2) if Ker a £ Ker t, then a sends each right coset Hg of group G by its subgroup H = Ker a onto the only element wÎ W¢. Moreover, if the kernel Ker a = H of the mapping a is an invariant of the group G and H £ Ker t, then: a) the crossed
quasi-homomorphism
a sends each left coset gH
onto the only element w Î W¢;
c) by the accompanying
homomorphism t: G ®
Aut
W all elements gh ÎgH
generate the same automorphism Any semi-junior group G(Wq) of Wq-symmetry can be derived from its generating group G and group W = `Õgi Î GPgi, knowing the kernel H1 of accompanying the homomorphism t: G ® Aut W of right conjugation, by the following steps: 1) to construct a crossed quasi-homomorphism a of the group G onto the non-trivial subgroup W¢ of W by the rule a(g) = w; 2) to combine pair-wise each g of G with each w = a(g); 3) to introduce
into the set of all these pairs the operation (4) [27-29].
Example 7. The "ïndexed" figure represented
in Figure 7 is described by the pseudo-junior group of
Wq-symmetry
G(Wq)
= (w01, w02,
w4, w4-1),
where w0 = <
e1,
e4,
e2,
e4-1> is unit of the group
W = P1 × P4
× P2 × P4-1 with P
= (e, p1 = (1234), p2
= (13)(24), p3 = (1432))
@C4
and w = <
p11,
p34,
p12,
p34-1> . In this case
We note that the "ïndexed" figure represented in Figure 8 is described by the semi-junior group of Wq-symmetry
9. The generalized crossed quasi-homomorphisms and the middle groups of Wq-symmetry Let us have the group G, the finite group W
= Õgi Î
GPgi
(where Pgi
@ P),
its subgroup V, the isomorphic injection f:
G®
Aut
W by the rule f(g) =
We note that in the case of V = w0
the generalized crossed quasi-homomorphism Any middle group G(Wq) of Wq-symmetry with the finite group W and the subgroup V of W-identical transformations can be derived from its finite generating group G and the group W = Õgi ÎGPgi of multi-component permutations by the following steps: 1) to find
in W all proper 2) to construct
a generalized crossed quasi-homomorphism 3) to combine
pair-wise each g of G with each w¢
of Vw = 4) to introduce into the set of all these pairs the operation (4) [28-33]. Remark that in operation (4) there are two different automorphisms
References [1] Zamorzaev A.M., On the groups of quasi-symmetry (P-symmetry). Kristallografiya, 1967, 12, no.5, p.819-825 (in Russan).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

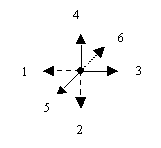

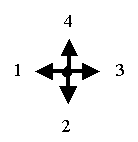
 G1
but H ¹ G) and with the subgroup
V1
of W-identical transformations (where V1 = V
Ç
Diag
W).
G1
but H ¹ G) and with the subgroup
V1
of W-identical transformations (where V1 = V
Ç
Diag
W).