(a)
(a) 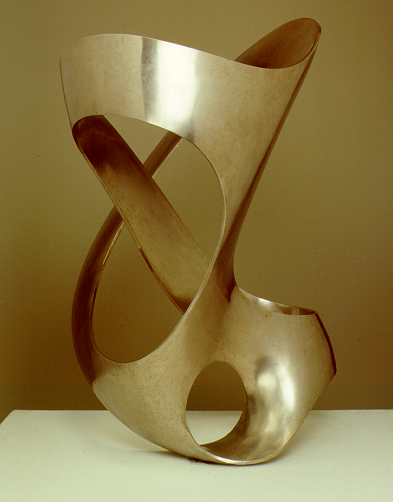 (b)
(b) Figure 1
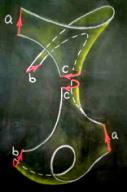
However, by considering the compact surface represented
by the sculpture, we show that it is topologically equivalent to the connected
sum of three projective planes with a point removed, corresponding to
the only boundary component of the represented surface.
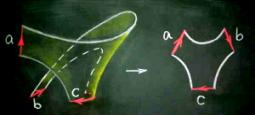
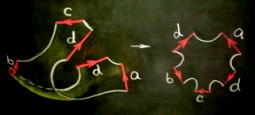
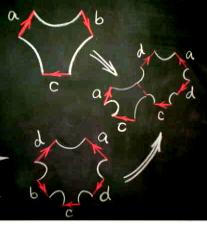
To prove this, we cut the surface into pieces in order to obtain a plane model and then we read its word and hence identify the compact surface represented.
The reader can find a brilliant account on plane models and words of compact surfaces without boundary (closed surfaces) in Massey’s book [WM], see also Carter’s book [SC]. For surfaces with boundary, we consider the word of the surface obtained by gluing discs along the boundary components. For instance, the Möbius band and the projective plane have the same associated word, that is, aa (Fig. 2).
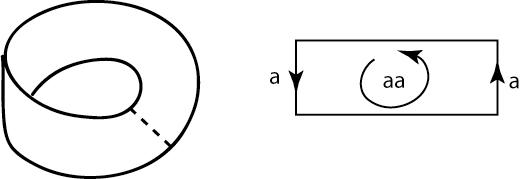
Figure 2
To prove this, we cut the surface into pieces in order to obtain a plane model and then we read its word and hence identify the compact surface represented.
The reader can find a brilliant account on plane models and words of compact surfaces without boundary (closed surfaces) in Massey’s book [WM], see also Carter’s book [SC]. For surfaces with boundary, we consider the word of the surface obtained by gluing discs along the boundary components. For instance, the Möbius band and the projective plane have the same associated word, that is, aa (Fig. 2).

Figure 2
 (a)
(a)  (b)
(b) 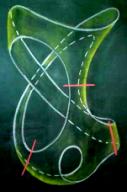 (c)
(c) 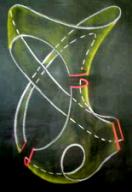 (d)
(d) 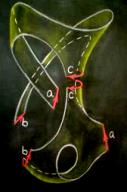 (e)
(e)