 |
 |
 |
 |
 |
 |
This paper illustrates with pictures and words how no-sew mathematical quilts provide opportunities to draw teachers into discussions of deep-level mathematics while engaged in an accessible artform that can brighten their classroom décor. Beyond explaining the construction of no-sew mathematical quilts and where one can get ideas for mathematical quilt patterns, we present the case of a practicing teacher and the insights she drew from developing her quilt. In doing so, we illustrate that by being open to explore mathematics in new and visual ways, no-sew mathematical quilts can enliven the mathematics classroom while providing opportunities for in-service teachers to engage with mathematics in new ways.
Quilting and mathematics, what do they have in common you might ask? Gibson and Thomas (2005) suggested that combining writing and the exploration of quilt patterns helps high school geometry students come to a better understanding of triangle congruence, reflections and transformations. But is that the extent of the potential benefits of incorporating the investigation of quilting in the mathematics classroom? Paznokas (2003) argued that there was much more that can be drawn from such examinations of quilting when she said, "Not only can quilts help teach multicultural history, literacy, and art, but quilting also provides a perfect and enjoyable tool for teaching mathematics concepts" (p. 250). Although Gibson and Thomas (2005) and Paznokas (2003) were focused on mathematical connections such as symmetry, transformations, ratios, patterns, tessellations, and fractions, quilts can also be used to explore higher-level mathematical ideas that touch concepts at the high school level and even beyond. For instance, the Quaternion Quilts described by Fisher (2005) certainly extend beyond high school mathematics to demonstrate group theoretic relationships from abstract algebra and the fractal quilts designed by Rose Rushbooke (2007). However, if one wished to be somewhat less esoteric, the two books by Venters and Ellison (1999, 2003) entitled Mathematical Quilts and More Mathematical Quilts provide quilt ideas more attuned to visualizing mathematical concepts in high school mathematics such as the Pythagorean Theorem, Fibonacci Sequence, Tessellations, Pascal's Triangle, Polar-coordinate graphs, and simple fractals.
Certainly in a mathematics classroom, sewing machines are not available thereby necessitating the need for a way to represent quilting ideas in a manner that expresses the quilt but does not requiring sewing. Both Venters and Ellison (1999) and Gibson and Thomas (2005) suggested colored construction paper or fabric and affixing these to poster board. We would extend that idea to include collecting various wallpaper patterns or scrapbook papers and using these as the "fabric" to build quilts. However, the resulting quilts using paper and glue do not have the dimensionality and finished look of real quilts. In this paper, we discuss how building no-sew quilts broadened students' understanding of mathematics and exposed them to deeper insights into higher-level mathematics. Specifically, we are going to look through the eyes of a practicing teacher as she took a graduate-level, professional development course. After that, we will briefly touch on some other potential impacts of no-sew mathematical quilts.
So, how can making a no-sew mathematical quilt entice a student to learn higher-level mathematics? Some might claim that making a quilt is just an art project but we claim that it is much more. To us, the quilt project is a conduit to get teachers intrigued and wondering about what they know and how it fits together with what they are doing. To illustrate this point, we are going to take excerpts from a practicing teacher that we will call Traci. Traci taught both at the high school level and collegiate level. She held a master's degree but was taking a graduate level course to expand her knowledge of how to visualize mathematics in new mediums.
When Traci was asked to select a quilt pattern as part of the inservice course, she explained her choice in the following way: "I picked this 'neat' circular pattern that looked something like a tessellation to me. To be honest, I just liked how it looked. I knew it was called the 'Poincaré Plane', and I knew that it looked like something like the tessellations that I had studied in previous years, but I had no idea what my quilt actually represented." That was the beginning of Traci's exploration into tessellations and more importantly, into what this higher-level mathematical idea of a Poincaré Plane might be.

Figure 2: Poincaré Plane Quilt
Let's step back for a moment. Traci recalled that her first experience with tessellations was when she took a Math for Elementary School Teachers course as an undergraduate and claimed that a tessellation "is created when a shape is repeated over and over again covering a plane without any gaps or overlaps." When Traci finished her undergraduate program, she was asked to teach a high school geometry course. When speaking about that experience, she said, "My second year of teaching, I was fortunate enough to teach geometry. I was so excited! I knew I wanted to show my students how to tessellate. Now teaching high school students about tessellations was going to be much different than thinking about the tessellations that I had done in college....These students were older, they needed to have a little bit more information about why tessellations work." This fact sent Traci to learn more about tessellations that were beyond the simple ones she had discussed as a college student thinking about teaching elementary school students. Through her experiences with kitchen and bathroom floor tiles, she envisioned that her high school students were older, wiser, and would ask deeper questions, questions that Traci wanted to be able to anticipate such as "why do tessellations work?" and "How do I figure out if a regular polygon tessellates?"
Traci's explorations answered her basic questions but in the midst of her explorations, she was drawn into a new world. She stated, "... while learning about and teaching tessellations, an artists name came up frequently, M.C. Escher. Who was this guy? The only thing that I knew about him was that he was a wonderful artist who made tessellations." Her excursions into Exploring the Infinite (Escher, 1986) took her from Escher's tessellations of the Euclidean Plane, such as those shown in figure 3, to stranger tessellations similar to those in figure 4.
 |
 |
 |
Figure 3: Examples of Escher's tessellations of the Euclidean Plane
 |
 |
Figure 4: Examples of Escher's tessellation on the Poincaré Plane
In each of the tessellations shown in figure 3, Escher tiled the Euclidean Plane with morphed copies of "regular" shapes that repeat to cover the plane without gaps or overlaps. In doing so, the artistic element was to deform those regular shapes into interesting objects that gave the perception of artistically rendered objects. The use of color, placement, and design made each tessellation interesting and unique. However, Escher did not restrict himself to tiling the Euclidean Plane, he also experimented with tiling on the Poincaré Plane also as shown in figure 4.
So, after seeing the tilings in figure 4, Traci made a connection and said, "Interesting enough, the tessellations looked oddly similar to the pattern that I had chosen for my quilt project. I had chosen a 'neat looking' pattern called the Poincaré plane. I had absolutely no idea who (or what) Poincaré was, but I knew that I liked this design for my quilt. I also knew that this design looked Escher-like." In fact, her quilt pattern, shown in figure 5, has distinct Escher-like qualities but more importantly, it serves as a nice characterization of the hyperbolic plane.
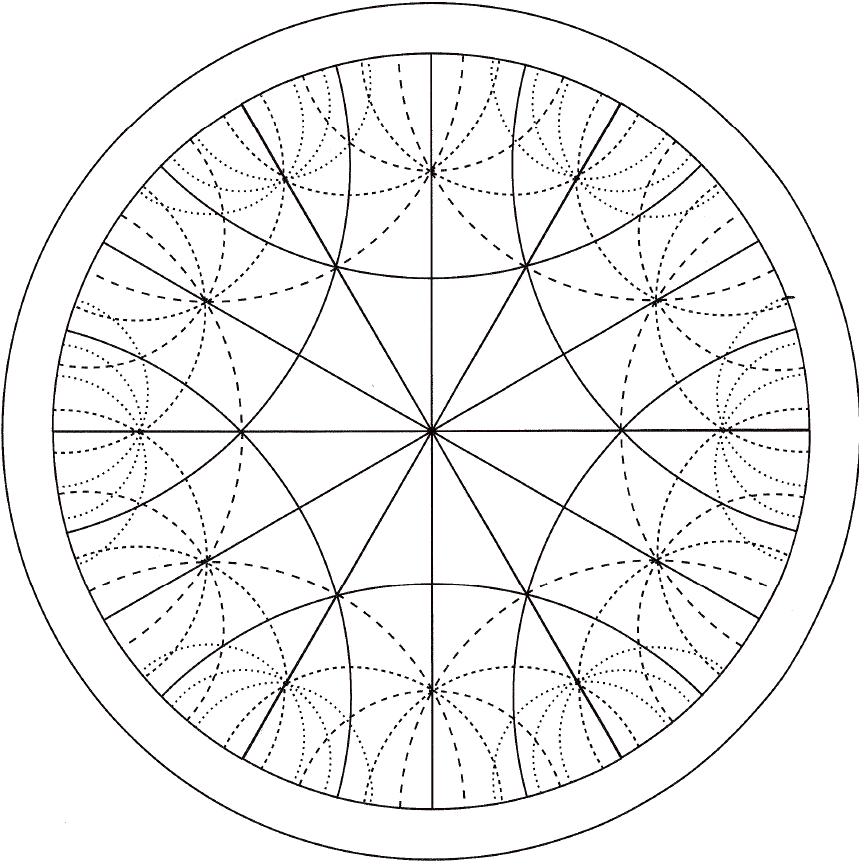
Figure 5: The Poincaré Plane quilt pattern from Venters and Ellison (2003)
As Traci contemplated her quilt, she struggled with a few things. In particular, she stated, "The quilt is a Poincaré plane and definitely a tessellation, but it is not what I am used to. The shape seems to repeat itself, yet the size is not the same each time. The pattern seems to go on forever. Or, it would go on forever, if it physically could go on forever.... So, is this Poincaré plane really a tessellation?" That question vexed Traci and caused her to delve deeper into mathematical concepts through additional research. When investigating Poincaré, Traci learned a considerable bit about his life and his contributions reached beyond mathematics to include, as Traci put it, "optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, theory of relativity, and cosmology." But of greater importance is that Traci learned that Poincaré worked with a conceptual model of the hyperbolic plane. She came to learn, "While there are only three regular polygons that tessellate the plane [equilateral triangle, square and hexagon, author inserted], there are infinitely many regular tessellations of the hyperbolic plane." In fact, Traci learned a new notation, Shalafi symbols, as a means of describing tessellations where "...{3,6} representing six [equilateral] triangles meeting at one vertex, {4,4} representing four squares meeting at one vertex, and {6,3} representing three hexagons meeting at one vertex." Here the Schalafi symbol {n,k} denotes a polygon of n sides meeting k times at a vertex. Traci then learned from Joyce (1998), "To determine whether {n,k} will (or will not) tessellate, simply look at the sum 1/n + 1/k. If the sum equals 1/2, the polygon tessellates the Euclidean plane. If the sum is greater than 1/2, the polygon tessellates the elliptic plane, and if the sum is less than 1/2, the polygon tessellates the hyperbolic plane."
So through her investigations, Traci came to the final conclusion that "... my Poincaré Plane is a tessellation, but not of the Euclidean plane, but of the hyperbolic plane. My quilt ... represents the hyperbolic plane. My quilt is an example of a {4,6} tiling, or tessellation. That means that each shape has four sides and that at any vertex six shapes meet. Compare this to the Euclidean plane. First of all, yes, a four sided figure can tessellate, but at any vertex, there are only four shapes that meet, not six." Such a revelation opened a whole new world to Traci but at the same time, such insight humbled her for she stated, "I have learned a lot about tessellations over the past few years, from being a college student to being a teacher, and back to being a student again. However, based on the information that I have learned on Poincaré, I realize that there is a lot more information out there, specifically on tessellations not on the [Euclidean] plane." Such insights gave Traci cause to continue to expand her understanding of tessellations and the underlying principles that impact the ability to realize tessellations in various geometries. (For a more thorough discussion of hyperbolic Escher patterns, see Dunham (1999))
Certainly, this is not the only no-sew mathematical quilt that can draw students into exploring higher-level mathematics. For instance, another teacher in the professional development course liked a brain teaser he found and decided to build a 2.5' x 4' quilt using that pattern (see figure 6). Somewhere inside the pattern is a regular five-pointed star (see figure 11 at the end of the paper for its location). This quilt top was designed using only four fabrics and provided the quilter the ability to discuss the classic four-color problem dealing with coloring a map with only four colors so that none of the borders have the same color. In contrast, the quilter of the Proofs of Pythagoras quilt (see figure 7) was a middle school mathematics teacher who wanted to have a 1' x 2' quilt that would help her students understand two different proofs of the Pythagorean Theorem. The top quilt block was taken from the Behold! quilt and the bottom quilt block displays a2 + b2 = c2 with the patriotic triangle serving as the center of the block.
 |
 |
|
|
|
Two other teachers chose to make 3' x 3' quilts based upon the Spiraling Pythagorean Triple Quilt design, shown in figures 8 and 9. This quilt was inspired, according to Venters and Ellison (1999), by the cover of the June 1989 Mathematics Magazine. In particular, the pattern is constructed by tessellating congruent triangles around the center to make a square and then larger squares are form by reflecting each triangle across its hypotenuse. In figure 8, the quilter decided to illustrate the tessellation with various hues of purple whereas the quilt in figure 9, was made using only 4 colors that were repeated within the quilt. This four-colored quilt brings to the foreground a visual spiraling motion whereas the purple colored quilt illustrates the spiraling by changing hues from light to dark. Both of these quilts led these teachers to learn more about Pythagorean triples and the quilter of the Purple Pythagorean Triple quilt discovered in her research that "The Babylonians had knowledge of these types of triangles at least 1000 years before Pythagorus.... The Babylonians were aware of at least 15 triples and it is believed that these triples could not have been found by trial and error." As part of her explorations, she gained historical perspective and deeper mathematical insights such as the formula that the Pythagoreans came up with:
Unfortunately, this formula only gives the odd triples. An associated formulas by Plato,
yields more of the triples but does not help find them all since it does not find any triple where the hypotenuse is greater than the leg by 1. Euclid developed the following formula to find the Pythagorean triples:
Such insights made the patterns in the quilts have greater meaning and provided interesting historical context for the inservice teachers.
 |
 |
|
Purple Spiraling Pythagorean Triple Quilt |
Four-color Spiraling Pythagorean Triple Quilt |
So, now that we have embroidered a tapestry of some of the mathematical insights that can arise after building a no-sew mathematical quilt, we want to explain how to build them. We suggest using fabric and one-inch think insulation board that can be obtained at a local home center in 4' x 8' sheets. The insulating foam board serves as the batting layer between the backing and quilt top. The quilt top is designed from any pattern that is cut into the insulation board and the fabric tucked into the cut seams held in place by friction. As a consequence, no glue or pins are needed to affix the fabric.
Quilting in this way is considerably easier and quicker than developing a quilt using the traditional method; however, quilts made from the foam board are not comfortable to sleep under even though they are insulating! The following series of snapshots shown in figure 10 illustrates the various stages of a mathematical quilt being developed. In particular, the 2' x 2' quilt shown in figure 10, entitled The Indiana Puzzle Quilt and also known as the Snail's Trail Pattern, is categorized by Venters and Ellison (1999) in the genre of a spiral quilt. In particular, this quilt is based upon Baravalle spirals which nest inscribed similar squares to form a logarithmic spiral. The synergistic pattern formed by the spirals capitalizes on the structure of the sixteen squares and the rotating four-patch in the center of each square. The resulting self-similarity provides opportunities to begin to talk about simple fractal patterns although this pattern is not a true fractal since the shape is not repeated only the steps are repeated.
 |
 |
|
Making the cuts |
Back attached and quilt top begun |
 |
 |
|
Starting the second color |
A completed quilt |
Figure 10: Stages of quilt construction
Click here to see a movie of this no-sew mathematical quilt being built
So, what exactly does one do to build a no-sew mathematical quilt?


We recognize that only a brave, or perhaps foolish, math teacher at the high school or middle school level would directly translate this professional development activity with adults into their classroom when it includes sharp x-acto knives. If one wishes to modify the activity to remove the x-acto knives from the classroom, it can be accomplished by having the students mark their patterns onto the foam boards and then for homework have them cut the patterns into the boards or the teacher can do this (it is actually quite cathartic). But if you have any concerns about x-acto knives in general, one can simulate the activity by using glue to affix wall paper patterns to the board instead of fitting the fabric. What we suggest is that teachers construct these no-sew mathematical quilts since they certainly will brighten the classroom and in doing so both the students who view them and the teachers who made them will be drawn to explore mathematics in new and different ways.
Consequently, we agree with Gibson and Thomas (2005) who said, "Each time a student sees a quilt, instead of sleeping under it, she may find herself analyzing it geometrically" (p. 111). However, we think that investigations into no-sew mathematical quilts can take her beyond geometry and lead her into new and amazing worlds of mathematics that typically are not mentioned at the high school level since there has not been easy ways to introduce them. This article has attempted to illustrate with pictures and words that constructing no-sew mathematical quilts is beneficial as an inservice activity for it not only provides opportunities to draw teachers into discussions of deep-level mathematics but also brightens the décor. Getting students to envision mathematical concepts in a variety of ways is essential to good teaching and enhances student learning. Mathematical quilts in the classroom set the stage for investigations and challenges by providing access to strong visual images that illustrate important mathematical concepts. We think the saying should be changed to: A quilt is worth a thousand words!

Figure 11: Location of the hidden star
Escher, M.C. (1986). Exploring the Infinite. New York, NY: Henry N. Abrams.
Dunham, D. (1999). Transformation of hyperbolic Escher patterns. Visual Mathematics, 1(1), [on-line serial]. Available online: http://members.tripod.com/vismath/dunham/index.html
Fisher, G.L. (2005). The Quaternions Quilt. FOCUS, 25(1), 4-5.
Gibson, M. & Thomas, T.G. (2005). Quilt blocks: Writing in the geometry classroom. Mathematics Teacher, 99(2), 108-111.
Joyce, D.E. (1998, December). Hyperbolic Tessellations. [on-line serial]. Available online: http://aleph0.clark.edu/`djoyce/Poincaré.html
Paznokas, L.S. (2003). Teaching mathematics through cultural quilting. Teaching Children Mathematics, 9(5), 250-25.
Rushbrooke, R. (2007). The art of Rose Rushbrooke: Where art meets science [website]. Available online: http://www.roserushbrooke.com/index.html
Venters, D. & Ellison, E.K. (1999). Mathematical Quilts. Emeryville, CA: Key Curriculum Press.
Venters, D. & Ellison, E.K. (2003). More Mathematical Quilts. Emeryville, CA: Key Curriculum Press.
 |
 |
 |