Moiré fringes are visually observed when two periodic (like a comb) or non-periodic (like a bar code) 2D grids or dots arrays are coplanarly superimposed and rotated as Figure 1a),1b) and 1c). Moiré fringes pattern obeys two main rules: 1º) Transverse Translation. It means that moiré fringes moved perpendicular to the bisector of the grids, preserving the sign of the displacement, at it is show in Figure 2a) and 2b), and 2º) Symmetry. It means that if one of the grids is turned face down and coplanarly superimposed and rotated again to the other grid, moiré pattern is still observed, as in case of evolutes at Figure 3a) and 3b). This paper deals with the observation of quasi-moiré patterns generated when two equal 2D transparencies containing any type of structures, like geometrical figures or even photographic pictures, are coplanarly superimposed as in grids or dots arrays cases [1,2,3]. Visual observations using i) non-perpendicular biperiodic grids, ii) periodic (x) - random (y) grids, iii) completely random grids, iv) and fractal grids were analysed. Examples of these types of 2D transparencies are: i) an array of alphabetic ordered Greek letters in successive lines, but introducing some displacement between letters from one to the next line (see Figure 4a) and 4b)), ii) a CD magnified area, on which tracks are 1.6 mm periodically spaced, and recorded signals look as a random array (see Figure 5a) and 5b))[4], iii) a magnified metallographic picture showing the grain structure (see Figure 6a) and 6b)), and iv) any natural or prepared fractal [5] picture (see Figure 7a) and 7b)), respectively.
When two identical transparencies T1 and T2 of the grain structure of a metal are coplanarly superimposed and the upper one is rotated an angle + a against the other, the quasi-moiré pattern observed consists of circles centred at the centre of rotation as in Figure 6a). The wider the rotation angle is, the smaller the radius of the entire circular quasi-moiré pattern results. This means that the observation of the circular quasi-moiré pattern depends on the degree of resemblance between details in both transparencies. As it is obvious, its centre is located where the degree of resemblance is higher. Also, if the rotated transparencies are relatively displaced along the ± x-axis or the ± y-axis, the circular quasi-moiré pattern moved along the ± y-axis or ± x-axis, respectively. Then, it means that the Transverse Translation rule is verified. But if one of the transparencies is turned face down and coplanarly superimposed again onto the other and rotated any angular value, the circular quasi-moiré pattern is not observed at all. So, the Symmetry rule does not hold any more, because the degree of resemblance between transparencies is zero, as it is demonstrated in Figure 6b). For this reason this pattern was called quasi-moiré pattern, because it obeys the first main rule on Transverse Translation, but not the second one related to the symmetry. As an example of the Transverse Translation rule, the animated Figure 8 shows a picture of the circular quasi-moiré pattern obtained by superposition and rotation of transparencies T1 and T2.
There are two more experimental observations using the same type of transparencies that can be explained in the insight of the degree of resemblance concept. Superimposing an original transparency on a scaled replica of itself can perform the first experiment. Both operations result in the observation of a radial quasi-moiré pattern, whose centre of dispersion is placed in a point where the degree of resemblance between details in both transparencies is higher. The area covered by the radial quasi-moiré pattern depends upon the scaling factor between transparency as it is demostrated by de animated Figure 9 . The higher the scale percentage is, the smaller the radius of the radial quasi-moiré pattern results. Of course, in this case the Transverse Translation rule is reduced to a Longitudinal Translation rule (see the animated Figure 10 , as it occurs when a Ronchi linear grid is perpendicularly displaced to its traces onto a scaled replica of itself. Let be a scaled up, i.e. + 10 %, transparency onto the original one. A relative displacement between both transparencies along the ± x-axis or the ± y-axis will produce the longitudinal translation of the radial lines quasi-moiré pattern along the m x-axis or the m y-axis. On the other side, let be a scaled down, i.e. - 10 %, transparency onto the original one. Then, a relative displacement between both transparencies along the ± x-axis or the ± y-axis produces the longitudinal translation of the radial quasi-moiré pattern along the ± x-axis or the ± y-axis. Summarising this observational facts, it results that all-relative transparency displacements will produce the higher degree of resemblance at the centre of the radial quasi-moiré pattern. However, the Symmetry rule does not hold as in the case of the circular quasi-moiré pattern.
The second experiment can be performed after the observation of the radial quasi-moiré pattern by rotating one of the transparencies against the other. In this case, the radial quasi-moiré pattern turns to multiple logarithmic spirals quasi-moiré pattern, whose centre is placed in the centre of the radial pattern, that is, where the degree of resemblance between details in both transparencies is higher. The arms of the spirals are developed according to the sign of the rotation angle and the sign of the scale factor between transparencies. For example, clockwise arms are developed when the upper transparency is rotated - a , and vice-versa, counterclockwise arms are observed with + a rotation angle as it is shown in the animated Figure 11. In this case, the Translation rule results as a vector composition between the circular quasi-moiré pattern rule and the radial lines quasi-moiré pattern rule. So, it means, for example, that displacements of one transparency along the ± x-axis will produce translations of the spirals centre along lines that are inclined with respect to the x-axis according to the sign and value of the scale factor and the sign and value of the rotation angle a between transparencies, as it is demostrated in the animated Figure 12. Besides, the Symmetry rule does not hold in any case.
a) Degree of resemblance and correlation
The quantitative evaluation of the degree of resemblance between transparencies is presented. If the structure contained in the transparency could be expressed as a mathematical function f(x,y), the degree of resemblance can be defined as the correlation function f * f , according to the expression:
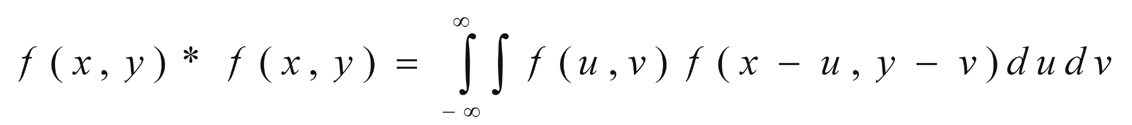
[6] as in the case of moiré patterns generated by the superposition of periodic grids.
b) Geometry and fractality
he set of spirals that emerges when both operations are performed, that is, scaling and rotation, are of logarithmic type. In fact, any point in the original or master transparency T1 located at a distance r measured from an arbitrary point O, is displaced in its replicated transparency T2 a distance Dr along the straight-line defined by the vector (O, r), and transversely displaced a distance r.Dj , where Dj is the rotation angle between transparencies around O. Then, the position of all those pairs of points are related by the differential equation:
dr = m. r.dj . (2)
It corresponds to the general formula:
r = ri . exp[ m ( j +ji -Dj )], (3)
of a set of logarithmic spirals in the polar coordinates (r,j). Each set of logarithmic spirals is characterised by its origin O -which is the centre of maximum correlation or high degree of resemblance between motifs- and the scaling parameter m between both transparencies, as well as Dj, the rotation angle between transparencies. Inside this set of spirals, each logarithmic spiral is characterised by the pair (ri ,ji), where ri is the position of the nearest point to the origin O in the master transparency at the angular position ji. The geometrical and analytical representation at Figure 13 describes the spiral set that emerges according to formula (3). It is important to remark that this mathematical law is completely independent of the type, shape or size of motifs on the master transparency. In fact, the distribution of motifs in transparencies employed to observe emergent quasi-moiré patterns, and the motifs themselves, are of different types, shapes and sizes. For instance, all Greek letters were printed in Figure 4a) and 4b) in a non-perpendicular biperiodic array, while in Figure 5a) and 5b) CD tracks are equally spaced while blanks, dots and bars look as a random distribution of motifs. Motifs at Figure 6a) and 6b) are differently sized and shaped and randomly distributed, while in Figure 7 the entire fractal motif is well mathematically defined. So, in spite of the fact of the tremendous differences between these examples, always a pair of correlated points exists that forms a cluster and allows us to observe quasi-moiré patterns.
An interesting remark is the fact that in making translation, rotation and scaling operations between the master transparency T1 and the translated, rotated and scaled transparency T2, always a logarithmic spiral will emerges inside the complete set of logarithmic spirals. Then, equation (3) shows that rotation operation and scaling operation are reciprocal among them. This curious property was analysed by Jacob Bernoulli, and it is intimately related to fractals: Logarithmic spirals are self-similar [7].
c) Quasi-moiré patterns emergence and percolation
Equation (3) has two different mathematical limits. One of the limits corresponds to the case on which the scaling factor is null, that is, m = 0. So, it means that the size of both transparencies, T1 and T2, is the same. Then, by rotating one transparency over the other the formation of clusters of correlated pairs of motifs allows the emergence of a set of circular quasi-moiré patterns, as in the animated Figure 8 . The second limit is related with the rotation angle Dj. If Dj = 0 and m ¹ 0, by superimposing the scaled-up or -down T2 transparency over the T1 master one, radial quasi-moiré patterns are observed, as in the animated Figure 9 . Besides, other kind of limitation affects the emergence of quasi-moiré patterns if the sizes of transparencies are taking into consideration. For instance, if the scaling parameter is larger than 20 % and the rotation angle is larger than 20º, radial, circular, and spiral quasi-moiré patterns are not clearly longer observed. It means that correlation between pairs of points at any place in transparencies falls down to zero. Only in the arbitrary point O the degree of resemblance between transparencies is high, but such a fact is not enough to decide which type of quasi-moiré patterns should be observed if experimental conditions are fulfilled. Then, in principle, it could be possible to introduce a density function D of clusters of correlated points that represents this experimental fact. Such a D function has its maximum value at O; and there must be normalised adopting the unit value. In order to make a relation between the maximum and the minimum values of the D function, it is convenient to the extent of this discussion, to place the point O at the centre of transparencies. Then, at the border R of transparencies the D function must adopt the minimum value. As the function D will reflect a sort of geometrical phase transition -as in percolation phenomenon- from its maximum value at O, and its minimum at the border of transparencies, such a limit or interface could be conveniently adopted at rl. Then, the D density function can be defined as: .
![]()
Figure 14 gives a representation of D for two values of m.
This paper deals with the observation of quasi-moiré patterns of different types: circles, radial lines and logarithmic spirals. Quasi-moiré patterns emerge when two transparencies representing any type of images -one original and its copy- are coplanarly superimposed and one of them rotated around an axis that is perpendicular to the plane of transparencies. Seeing through a transparency its coplanarly rotated copy the observer sees circular quasi-moiré patterns. If the copy is scaled-up or -down, the observer sees radial quasi-moiré patterns; and if this copy is coplanarly rotated against the original transparency, the observer sees logarithmic spirals.
X or y displacements of one of the transparency produce transverse or longitudinal translation of the quasi-moiré pattern or a vectorial sum of them, according with Translation rules for moiré patterns. But quasi-moiré patterns do not obey the Symmetry rule, which is followed by regular moiré patterns. If two observers are seeing through coplanarly superimposed transparencies in opposite ways -that is, perpendicularly to the transparency plane but from each plane sides- they will see complementary quasi-moiré patterns. The relevant case is that corresponding to logarithmic spiral quasi-moiré patterns. In fact, one of the observers sees a logarithmic spiral quasi-moiré pattern clockwise developed, while the other observer sees the counterclockwise-developed spirals. Besides, the complementarity implies that both observers will see complementary movements of the centre of circular, radial and logarithmic spiral quasi-moiré patterns when one of the transparencies is displaced with respect to the other. The behaviour of quasi-moiré patterns is engaged with fractal attributes of translation, rotation and scaling of transparencies. Finally, the observation of quasi-moiré patterns is related with the percolation phenomenon through a density D function defined in equation (4).
This work received financial support from Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Comisión de Investigaciones Científicas de la Provincia de Buenos Aires (CIC), and Universidad Nacional de La Plata (UNLP), Argentina. Authors are indebted to K. and G. Videla for helping them in processing quasi-moiré pattern images. The Centro de Investigaciones Opticas depends from CONICET and CIC.
- M. Garavaglia, "Symmetry? Moiré vs Other Quasi-related Moiré Patterns", Book of Extended Abstracts - Part 1, pp. 43 - 46. Fourth Congress of the International Society for the Interdisciplinary Study of Symmetry, Technion, Haifa, Israel, 13 - 18 September 1998.
- M. Garavaglia, "Observing geometric figures quasi-related to moiré patterns", Poster 130, CD Proceedings of the III Ibero American Optics Meeting and VI Latin American Meeting on Optics, Lasers and their Applications, Cartagena de Indias, Colombia, 28 September-2nd October, 1998. CD edited by the Academia Colombiana de Ciencias Exactas, Físicas y Naturales, ISBN 958-9205-32-1.
- M. Garavaglia, "Quasi-moiré patterns observed when an original transparency is superposed to its scaled-up and -down transparencies", Optics and Optoelectronics: Theory, Devices and Applications, Editors, O. P. Nijhawan, A. K. Gupta, A. K. Musla and Kehar Singh, Volume 2, pp. 1149-1153. Narosa Publishing House, New Delhi, Madras, Bombay, Calcutta and London, 1998.
- Figure 4 from M. Mansuripur, C. Peng, J. K. Erwin, W. Bletscher, S. G. Kim, S. K. Lee, R. E. Gerber, C. Bartlett, T. D. Goodman, L. Cheng, C. S. Chung, T. Kim, and K. Bates, "Versatile polychromatic dynamic testbed for optical disks", Applied Optics, 36, 9296-9303, 1997.
- Figure 5 from H. O. Peitgen, H. Jürgens and D. Saupe, "Chaos and Fractals. New frontiers of science" Springer, 1992, in which part of the B. Mandelbrot set is depicted. 6-
- R. Bracewell, "The Fourier Transform and its Applications", McGraw-Hill Book Company, 1965.
- H. O. Peitgen, H. Jürgens and D. Saupe, "Chaos and Fractals. New frontiers of science" Springer, 1992.